"giving a y vector that is parallel to the 2 projected vectors."

Clearly I meant to write perpendicular.

Post a reply to this message

"BW: since this is before we do any projection, and we're only testing height
and
width, can't we have a slanted ray that WOULD intersect the sor spline once it
got rotated around the y-axis?"

This was meant to be deleted, after I had worked all that out.

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:

>     MInvTransPoint(P, ray.Origin, Trans);
>
>     MInvTransDirection(D, ray.Direction, Trans);


Now I can't really find if and where Trans gets defined as anything but an
Identity matrix in Line 776.

The sor gets created "at the origin" / around the y-axis,
so I'm now presuming that when we do
sor { ... translate <x, y, z>}

that the sor gets created and evaluated in its default position, and then all of
the results just get filtered through the translate transform as a
post-intersection process.

And if THAT's the case, then why do we have all of the transforms in the various
functions when we don't need them?

But then again, I could be missing something, and be completely wrong.

- BE

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:

> a is the squared length of the direction vector
> which, if non-zero, the vector cross product length gets divided by,
> which should be the shortest, perpendicular length.

a is the squared length of the PROJECTED direction vector

> A few minor problems.
> The ray direction vector already gets normalized at the beginning of
> Sor_Intersect, so why are we calculating it's length again, and then checking if
> it's more than zero, when at this point it should always be ONE.

Because although the RAY is normalized, it's PROJECTION isn't unit-length unless
it's parallel to the xz plane.

> Which bring up the potential divide-by-zero error when the normalization
> calculation is done - and there is NO checking THERE!
> And then there is the vector cross product sign issue.
>
> So, after this gets rigorously checked, I'd suggest that
> 1. the ray direction vector length check gets moved to earlier in the code

> 3. Line 276 r0 = P[X] * D[Z] - P[Z] * D[X];
> should be r0 = fabs(P[X] * D[Z] - P[Z] * D[X]);
> so that the "length" is always positive.

- BE

Post a reply to this message

"Bald Eagle" <cre### [at] netscapenet> wrote:

> r0 = P.x * D.z - P.z * D.x;
> and that is only multiplied by the y unit basis vector,
> so since there are no other dimensional units, this directly evaluates to the
> length of the perpendicular y vector, and we don't have to do the expensive
> square root of the sum of the squares.
>
> a is the squared length of the [NORMALIZED and PROJECTED] direction vector
> which, if non-zero, the vector cross product length gets divided by,
> which should be the shortest, perpendicular length.

So what happens is that the "perp dot product" is essentially taking one vector,
rotating it counterclockwise by 90 degrees, and then taking the dot product,
which projects one vector onto the other.
This gives its projected length along the other vector.

And that's supposed to give the perpendicular, shortest distance between the
origin and the ray.

Diagrammatically, it's all looking good, but for some strange reason, the
perpendicular distance seems to be shorter than it should be, with the error
increasing the farther away the ray is.

- BW

If anyone has any ideas what the source of this error is, I'm all ears.

Post a reply to this message

Attachments:
Download 'sor_diagram1.png' (130 KB)

Preview of image 'sor_diagram1.png'

GOT IT.

OK, so I am pretty confident that I have the whole initial bounding-test section
of the code worked out.

And that has led me to prove that one problem I thought was happening IS
happening,

and

there's another issue that is taking place that might explain why sometimes some
of the segments fail to render.

> Diagrammatically, it's all looking good, but for some strange reason, the
> perpendicular distance seems to be shorter than it should be, with the error
> increasing the farther away the ray is. (*)

1. The rays that give a negative perpendicular dot product erroneously test as
hitting the bounding cylinder, and so a bunch of root solving gets done that
shouldn't be.

1a.  The code tests a bounding cylinder that is based on the largest diameter of
the whole sor {}.   But the sor {} is not so much a single object as it is a
stack of individual segments.
I believe that we ought to be testing intersection with each individual segment
to optimize the bounding tests.

2. The issue (*) above was a result of the ray direction being used as-is.
When I had an angled ray, the length was too large, and overly shortened my
perpendicular vector.
When I only used the ray projection onto the xz plane, all of my perpendicular
vectors were of the proper length.

2a.  This too-short vector projection likely leads to false positives and causes
additional unnecessary root-finding.


So, I would like to propose 2 correction to this section of the sor {} source.

1. replace
D = ray.Direction;
with
D = <ray.Direction.x, 0, ray.Direction.z>;

and
2. replace
#if (r0 > Radius2)
with
#if (fabs(r0) > Radius2)


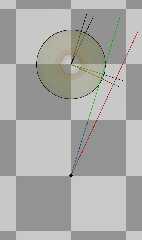
The attached diagram is a mess, but what we have is the sor {} circled in black
with the radius equal to the greatest x-value of the control points.

along the bottom, the ray origin changes, and the direction vector stays the
same, resulting in a sweep from left to right.  As you can (hopefully) see, the
parallel lines change from green to red.
The green lines signify a successful _intersection test_ of the ray with the
bounding cylinder.  The red are fails.
The thing to notice here is that only the misses to the right actually fail the
intersection test.
All of the rays on the left pass the test and go on to calculate the roots of
where the ray intersects the polynomial.

The fan shape above that is holding the ray origin fixed, while making the ray
direction go around in a circle 360 degrees.
The same false positive issue occurs.

Next post will fix that with fabs(r0)

Post a reply to this message

Attachments:
Download 'sor_diagram1.png' (524 KB)

Preview of image 'sor_diagram1.png'

"Bald Eagle" <cre### [at] netscapenet> wrote:

> Next post will fix that with fabs(r0)

As you can see, there is a lot more red in this render, showing the removal of
erroneous bounding intersection positives, and the rays fail on both the left
and the right now, with only the rays that actually intersect the bounding
cylinder triggering the root-solving phase.

Post a reply to this message

Attachments:
Download 'sor_diagram1.png' (522 KB)

Preview of image 'sor_diagram1.png'

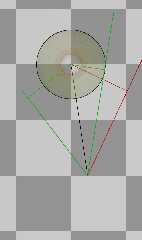
And here is a much simplified diagram showing only 3 rays, with all extraneous
lines removed.

Only the rays and the perpendicular distances are shown, color coded for
bounding intersection test state.

Post a reply to this message

Attachments:
Download 'sor_diagram1.png' (134 KB)

Preview of image 'sor_diagram1.png'

Desmos live graphing

Move the ray origin or the direction vector endpoint.
Very useful for working things out.

https://www.desmos.com/calculator/o50ybsmkw3

- BE

Post a reply to this message

On 10/9/25 22:08, Bald Eagle wrote:
> And here is a much simplified diagram showing only 3 rays, with all extraneous
> lines removed.
> 
> Only the rays and the perpendicular distances are shown, color coded for
> bounding intersection test state.
> 

I'm loosely following your sor updates - good work. I'll try and carve 
out some time to code up your suggested changes in my working yuqk code 
& do some testing.

Bill P.

Post a reply to this message