 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
the documentation for the transformation matrix says: "... you will not use the
matrix keyword because it is ... harder to visualize." however, although
"mathematically challenged", I'd like to learn to use it on occasion.
that in mind, can someone please explain why the manual (3.3.1.12.4) mentions a
"..fourth column implicitly set to <0,0,0,1>..", but the subsequent equations do
not include/use those values.
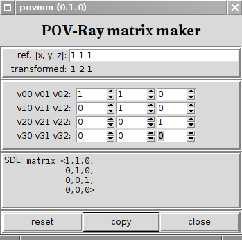
I've attached a WIP script, "POV-Ray matrix maker", a simpe UI which displays a
reference point and its transformation as per the matrix values given. the
recalculation takes place whenever the focus moves from one control to another
(ie <Tab> and <Shift-Tab>), the copy button places the current matrix (SDL) on
the clipboard. requires Tk.
feedback sought. enjoy.
regards, jr.
Post a reply to this message
Attachments:
Download 'povmm.tk.txt' (6 KB)
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"jr" <cre### [at] gmail com> wrote:
> ... focus moves from one control to another
> (ie <Tab> and <Shift-Tab>), ...
or mouse clicks. :-)
screenshot attached.
regards, jr. com> wrote:
> ... focus moves from one control to another
> (ie <Tab> and <Shift-Tab>), ...
or mouse clicks. :-)
screenshot attached.
regards, jr.
Post a reply to this message
Attachments:
Download 'povmm.png' (16 KB)
Preview of image 'povmm.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"jr" <cre### [at] gmail com> wrote:
> hi,
>
> the documentation for the transformation matrix says: "... you will not use the
> matrix keyword because it is ... harder to visualize." however, although
> "mathematically challenged", I'd like to learn to use it on occasion.
>
> that in mind, can someone please explain why the manual (3.3.1.12.4) mentions a
> "..fourth column implicitly set to <0,0,0,1>..", but the subsequent equations do
> not include/use those values.
Because all of those things are affine transform matrices.
IIRC, those other numbers change when you start to use projection matrices and
other transformations.
See:
http://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matri
ces-what-you-need-to-know-first
http://news.povray.org/povray.general/thread/%3Cweb.5b9ed475f76fb4baa47873e10%40news.povray.org%3E/ com> wrote:
> hi,
>
> the documentation for the transformation matrix says: "... you will not use the
> matrix keyword because it is ... harder to visualize." however, although
> "mathematically challenged", I'd like to learn to use it on occasion.
>
> that in mind, can someone please explain why the manual (3.3.1.12.4) mentions a
> "..fourth column implicitly set to <0,0,0,1>..", but the subsequent equations do
> not include/use those values.
Because all of those things are affine transform matrices.
IIRC, those other numbers change when you start to use projection matrices and
other transformations.
See:
http://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matri
ces-what-you-need-to-know-first
http://news.povray.org/povray.general/thread/%3Cweb.5b9ed475f76fb4baa47873e10%40news.povray.org%3E/
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Also, some of what is here may be of interest to read as supplementary material:
http://news.povray.org/povray.advanced-users/thread/%3C5bb67852%40news.povray.org%3E/
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"Bald Eagle" <cre### [at] netscape net> wrote:
> ...
>
http://news.povray.org/povray.general/thread/%3Cweb.5b9ed475f76fb4baa47873e10%40news.povray.org%3E/
thank you Bill. I forgot and, re-reading, now remember having followed that
thread when it began. :-(
regards, jr. net> wrote:
> ...
>
http://news.povray.org/povray.general/thread/%3Cweb.5b9ed475f76fb4baa47873e10%40news.povray.org%3E/
thank you Bill. I forgot and, re-reading, now remember having followed that
thread when it began. :-(
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 25.12.2018 um 18:18 schrieb jr:
> hi,
>
> the documentation for the transformation matrix says: "... you will not use the
> matrix keyword because it is ... harder to visualize." however, although
> "mathematically challenged", I'd like to learn to use it on occasion.
>
> that in mind, can someone please explain why the manual (3.3.1.12.4) mentions a
> "..fourth column implicitly set to <0,0,0,1>..", but the subsequent equations do
> not include/use those values.
The underlying mathematical operation of the matrix transform is a
multiplication of a vector (representing an original location) by a
matrix (the transformation matrix), yielding another vector
(representing the transformed location).
Now the simplest such operation would be a 3-component vector multiplied
by a 3x3-component matrix to yield a 3-component vector. However, such
an operation could only represent a true linear transformation - meaning
there could not be a translation component; the origin (<0,0,0>) would
always be mapped to itself.
Transformations can be "bolted on" to this concept (leading to what is
called "affine transformations") by complementing the matrix with a
3-component vector that is added after the matrix multiplication.
The resulting data structure can be considered a 4x3 matrix, with the
last row[*] having special semantics: While the other rows are
multiplied with the respective coefficient of the original vector, this
last row is added "as is", without any multiplication.
Alternatively, we can pretend that the 4th row is multiplied by 1 before
adding. We can also pretend that this factor of 1 is a 4th component of
the original vector.
It turns out that this idea can be taken even one step further, by using
4-component vectors all throughout (with the 4th component being fixed
to 1), and a 4x4-component matrix. To make this work, the last column[*]
of such a matrix must also be fixed, and have the coefficients {0,0,0,1}.
(It should be noted that this is just a fancy way of looking at the very
same algorithm, some magic sleight of hand to soothe people with OCD.)
[*There is disagreement between mathematicians and computer graphics
people about how to write matrices; where one faction uses columns and
rows, the other instead uses rows and columns, respectively.]
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
clipka <ano### [at] anonymous org> wrote:
> Am 25.12.2018 um 18:18 schrieb jr:
> > that in mind, can someone please explain why the manual (3.3.1.12.4) mentions a
> > "..fourth column implicitly set to <0,0,0,1>..", but the subsequent equations do
> > not include/use those values.
>
> ...
> The resulting data structure can be considered a 4x3 matrix, with the
> last row[*] having special semantics: While the other rows are
> multiplied with the respective coefficient of the original vector, this
> last row is added "as is", without any multiplication.
> ...
thank you v much for the detailed explanation. so the 4th column is the
optional extra that allows the translation wrt "surrounding" space?
I will need to abstract your reply (and Bald Eagle's reminders), write it out in
my own words in the hope it'll sink in.
regards, jr. org> wrote:
> Am 25.12.2018 um 18:18 schrieb jr:
> > that in mind, can someone please explain why the manual (3.3.1.12.4) mentions a
> > "..fourth column implicitly set to <0,0,0,1>..", but the subsequent equations do
> > not include/use those values.
>
> ...
> The resulting data structure can be considered a 4x3 matrix, with the
> last row[*] having special semantics: While the other rows are
> multiplied with the respective coefficient of the original vector, this
> last row is added "as is", without any multiplication.
> ...
thank you v much for the detailed explanation. so the 4th column is the
optional extra that allows the translation wrt "surrounding" space?
I will need to abstract your reply (and Bald Eagle's reminders), write it out in
my own words in the hope it'll sink in.
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()