 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 1-2-2024 om 13:42 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
> "A ritualistic purpose seems indicated."
>
> "it is completely unknown what the object represented or was used for, or in
>> what context, religious or other."
>
> I always find these ritual/religious explanations tiresome - Look around the
> modern world, and try to even count the number of knick-knacks, baubles,
> bric-a-brac, curios, ornaments, souvenirs, and trinkets people buy and
> accumulate - all of which have zero ritualistic or religious purpose or meaning.
>
Those /are/ 'ritualistic' in most cases my friend! ;-)
> It could have been a _designer_ dodecahedron that was very trendy, and only the
> wealthiest could afford then, to flaunt their status.
>
Quite possible indeed.
> If it was found with hordes, maybe the holes were used to measure coins to
> detect coin-shaving. I have solid state electronic scales and an electronic
> device to test the purity and composition of gold and silver alloys. None of
> which make any sense to a future civilization once the batteries were long gone.
> Granted, the alloy tester is $1000, but the scale is a cheapo mass-market thing
> that has no real inherent value, but is only used in proximity to coins, etc.
>
the batteries are certainly gone for this one!
> Maybe it was tabletop sign, to indicate membership in a trade guild.
>
I like that one.
> Maybe it was a tip jar. : >
<grin> Too many holes through where the tip could be lost.
> It could be an ancient "Challenge Coin" and the holes were to hold shotglasses.
> Maybe it held incense or pencils or quills.
>
no shotglasses at the time... perhaps shotgoblets.
> Perhaps it's a loupe, and the glass lenses are long gone. The knobs at the
> vertices held the device the proper distance from the surface being observed.
>
No. too far fetched. I don't think the Romans had lenses at all.
> Maybe it's a 12-sided die, and was used for gambling >
those things are generally 10 to 15 cm in diameter, cast in bronze...
the knobs get in the way.
> Maybe it was used by scammers to do zodiac astrological fortune telling.
>
Now, that is a thought...
> Perhaps it held an oil lamp, either for illumination, or as a distant forerunner
> of the USB coffee mug heater. Or a camp stove.
>
Hmmmm...
> Maybe it's a mandrel or a template for assembling something - perhaps with cord,
> and the holes are for aligning the loops of the developing knots.
>
well...
> It could be a neckerchief slide or similar fastening device.
>
..needing a strong neck indeed ;-)
> Has anyone blown into it? Maybe it's a whistle.
>
You can spit into it, but blow...? makes no sense.
>
>
>
> Perhaps we can only know its true purpose once it's been rendered sufficiently.
>
Yes, but certainly when discovered still more of them in different contexts.
> CSG-Dodecahedron challenge! Now for a cool Roman render rig as a backdrop!
>
Yep!
--
Thomas org> wrote:
>
> "A ritualistic purpose seems indicated."
>
> "it is completely unknown what the object represented or was used for, or in
>> what context, religious or other."
>
> I always find these ritual/religious explanations tiresome - Look around the
> modern world, and try to even count the number of knick-knacks, baubles,
> bric-a-brac, curios, ornaments, souvenirs, and trinkets people buy and
> accumulate - all of which have zero ritualistic or religious purpose or meaning.
>
Those /are/ 'ritualistic' in most cases my friend! ;-)
> It could have been a _designer_ dodecahedron that was very trendy, and only the
> wealthiest could afford then, to flaunt their status.
>
Quite possible indeed.
> If it was found with hordes, maybe the holes were used to measure coins to
> detect coin-shaving. I have solid state electronic scales and an electronic
> device to test the purity and composition of gold and silver alloys. None of
> which make any sense to a future civilization once the batteries were long gone.
> Granted, the alloy tester is $1000, but the scale is a cheapo mass-market thing
> that has no real inherent value, but is only used in proximity to coins, etc.
>
the batteries are certainly gone for this one!
> Maybe it was tabletop sign, to indicate membership in a trade guild.
>
I like that one.
> Maybe it was a tip jar. : >
<grin> Too many holes through where the tip could be lost.
> It could be an ancient "Challenge Coin" and the holes were to hold shotglasses.
> Maybe it held incense or pencils or quills.
>
no shotglasses at the time... perhaps shotgoblets.
> Perhaps it's a loupe, and the glass lenses are long gone. The knobs at the
> vertices held the device the proper distance from the surface being observed.
>
No. too far fetched. I don't think the Romans had lenses at all.
> Maybe it's a 12-sided die, and was used for gambling >
those things are generally 10 to 15 cm in diameter, cast in bronze...
the knobs get in the way.
> Maybe it was used by scammers to do zodiac astrological fortune telling.
>
Now, that is a thought...
> Perhaps it held an oil lamp, either for illumination, or as a distant forerunner
> of the USB coffee mug heater. Or a camp stove.
>
Hmmmm...
> Maybe it's a mandrel or a template for assembling something - perhaps with cord,
> and the holes are for aligning the loops of the developing knots.
>
well...
> It could be a neckerchief slide or similar fastening device.
>
..needing a strong neck indeed ;-)
> Has anyone blown into it? Maybe it's a whistle.
>
You can spit into it, but blow...? makes no sense.
>
>
>
> Perhaps we can only know its true purpose once it's been rendered sufficiently.
>
Yes, but certainly when discovered still more of them in different contexts.
> CSG-Dodecahedron challenge! Now for a cool Roman render rig as a backdrop!
>
Yep!
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 1-2-2024 om 14:28 schreef jr:
> Thomas de Groot <tho### [at] degroot org> wrote:
>>> did that before posting, ...
>> Oh, sorry! yes, that page was meant as a context.
>
> no worries. looks like I missed the second link you provided.
>
>
>> ... I am highly interested in archaeology, ...
>
> no kidding. first the vase, now this.. </grin>
>
> and that Wikipedia article disappointed a little in that there are no measures
> attached; _now_, of course, I've tons of questions. for instance, I'd like to
> know whether the circular openings are of the same sizes across unrelated finds,
> whether they appear to be in "straight" ratios to one another, etc, etc. strange
> that all of these museum items seem not even to have been looked at for
> "scientific study".
>
If I am correct, they are 10 to 15 cm diameter on the average
(grapefruit-size); I the TV show, it was said I believe that the holes
were not consistently identical in between different objects. Given the
differences in sizes, that seems probable. No straight ratios are
mentioned indeed and I have a hunch that there is none. They /were/
studied but except for the aspect, results were inconclusive...
--
Thomas org> wrote:
>>> did that before posting, ...
>> Oh, sorry! yes, that page was meant as a context.
>
> no worries. looks like I missed the second link you provided.
>
>
>> ... I am highly interested in archaeology, ...
>
> no kidding. first the vase, now this.. </grin>
>
> and that Wikipedia article disappointed a little in that there are no measures
> attached; _now_, of course, I've tons of questions. for instance, I'd like to
> know whether the circular openings are of the same sizes across unrelated finds,
> whether they appear to be in "straight" ratios to one another, etc, etc. strange
> that all of these museum items seem not even to have been looked at for
> "scientific study".
>
If I am correct, they are 10 to 15 cm diameter on the average
(grapefruit-size); I the TV show, it was said I believe that the holes
were not consistently identical in between different objects. Given the
differences in sizes, that seems probable. No straight ratios are
mentioned indeed and I have a hunch that there is none. They /were/
studied but except for the aspect, results were inconclusive...
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
Thomas de Groot <tho### [at] degroot org> wrote:
MichaelJF <fri### [at] t-online org> wrote:
MichaelJF <fri### [at] t-online de> wrote:
> If I am correct, they are 10 to 15 cm diameter on the average
> (grapefruit-size); ...
> I could only find the following measures (archived German site):
thanking you both. and yes, that German site on the Wayback machine answered
several of my questions (page "Funktion" in particular), curiously, the
manufacture ("Herstellung") page did not show.
cheers & regards, jr. de> wrote:
> If I am correct, they are 10 to 15 cm diameter on the average
> (grapefruit-size); ...
> I could only find the following measures (archived German site):
thanking you both. and yes, that German site on the Wayback machine answered
several of my questions (page "Funktion" in particular), curiously, the
manufacture ("Herstellung") page did not show.
cheers & regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> > I currently have my nose to the ground, trying to find an algorithm to generate
> > the inverse of a 9x9 rigid body transform matrix - if I can puzzle that out,
> > then any object specified with 4 points can be mapped to any other instance with
> > a transform {matrix{}} statement.
> > Then I can take one base, look over where it sits somewhere else in the helix,
> > and calculate exactly how to get it from one place to another.
> >
> That could be very useful. Also in a universal sense, applied to all
> sort of transformations/mutations.
OK, So I haven't ferreted out all the details of the purely matrix approach, but
while closing one of the 100 browser tabs I have open, I stumbled across a guy
using Reorient_Trans, and figured that would be a viable approach.
I had a few false starts due to not really being able to visualize what was
going on, but after making an IRL model and turning it around a few times, the
part I was missing / improperly implementing became obvious, and I was able to
package it all up into a single macro.
Identify any three points on your original object (A, B, C), and where those
three points end up (A2, B2, C2)
Apply the macro like so:
#declare MyTransform = Reorient_Triangle (A, B, C, A2, B2, C2)
object {MyObject transform {MyTransform}}
Please try this out with a large assortment of objects in various orientations
to see if I missed anything. The only thing not included is a sanity check for
plugging in a second set of coordinates that are identical to the first.
#macro Reorient_Triangle (A, B, C, A2, B2, C2)
// Bill Walker "Bald Eagle" February 2024
#ifndef(TRANSFORMS_INC_TEMP)
#include "transforms.inc"
#end
#local Translate1 = transform {translate -A}
#local Vector1 = B - A;
#local Vector2 = B2 - A2;
// Align Vector1 to Vector2
#local FirstTransform = transform {Reorient_Trans (Vector1, Vector2)};
#local A1 = vtransform (A-A, FirstTransform)+A;
#local B1 = vtransform (B-A, FirstTransform)+A;
#local C1 = vtransform (C-A, FirstTransform)+A;
// Find the vector to C1 that is perpendicular to Vector2
#local T1 = vdot (B1-A1, C1-A1) / vdot (B1-A1, B1-A1);
#local D = A1 + T1 * (B1-A1);
#local Vector3 = C1 - D;
// Find the vector to C2 that is perpendicular to Vector2
#local T2 = vdot (B2-A2, C2-A2) / vdot (B2-A2, B2-A2);
#local D2 = A2 + T2 * (B2-A2);
#local Vector4 = C2 - D2;
// Rotate everything around Vector2 so that the perpendicular vectors match
#local SecondTransform = transform {Reorient_Trans (Vector3, Vector4)};
// Now everything is similarly aligned with 3 sequential transforms
// and translating a final time puts the object at the destination
#local Translate2 = transform {translate A2}
#local T = transform { transform {Translate1} transform {FirstTransform}
transform {SecondTransform} transform {Translate2} }
T
#end org> wrote:
> > I currently have my nose to the ground, trying to find an algorithm to generate
> > the inverse of a 9x9 rigid body transform matrix - if I can puzzle that out,
> > then any object specified with 4 points can be mapped to any other instance with
> > a transform {matrix{}} statement.
> > Then I can take one base, look over where it sits somewhere else in the helix,
> > and calculate exactly how to get it from one place to another.
> >
> That could be very useful. Also in a universal sense, applied to all
> sort of transformations/mutations.
OK, So I haven't ferreted out all the details of the purely matrix approach, but
while closing one of the 100 browser tabs I have open, I stumbled across a guy
using Reorient_Trans, and figured that would be a viable approach.
I had a few false starts due to not really being able to visualize what was
going on, but after making an IRL model and turning it around a few times, the
part I was missing / improperly implementing became obvious, and I was able to
package it all up into a single macro.
Identify any three points on your original object (A, B, C), and where those
three points end up (A2, B2, C2)
Apply the macro like so:
#declare MyTransform = Reorient_Triangle (A, B, C, A2, B2, C2)
object {MyObject transform {MyTransform}}
Please try this out with a large assortment of objects in various orientations
to see if I missed anything. The only thing not included is a sanity check for
plugging in a second set of coordinates that are identical to the first.
#macro Reorient_Triangle (A, B, C, A2, B2, C2)
// Bill Walker "Bald Eagle" February 2024
#ifndef(TRANSFORMS_INC_TEMP)
#include "transforms.inc"
#end
#local Translate1 = transform {translate -A}
#local Vector1 = B - A;
#local Vector2 = B2 - A2;
// Align Vector1 to Vector2
#local FirstTransform = transform {Reorient_Trans (Vector1, Vector2)};
#local A1 = vtransform (A-A, FirstTransform)+A;
#local B1 = vtransform (B-A, FirstTransform)+A;
#local C1 = vtransform (C-A, FirstTransform)+A;
// Find the vector to C1 that is perpendicular to Vector2
#local T1 = vdot (B1-A1, C1-A1) / vdot (B1-A1, B1-A1);
#local D = A1 + T1 * (B1-A1);
#local Vector3 = C1 - D;
// Find the vector to C2 that is perpendicular to Vector2
#local T2 = vdot (B2-A2, C2-A2) / vdot (B2-A2, B2-A2);
#local D2 = A2 + T2 * (B2-A2);
#local Vector4 = C2 - D2;
// Rotate everything around Vector2 so that the perpendicular vectors match
#local SecondTransform = transform {Reorient_Trans (Vector3, Vector4)};
// Now everything is similarly aligned with 3 sequential transforms
// and translating a final time puts the object at the destination
#local Translate2 = transform {translate A2}
#local T = transform { transform {Translate1} transform {FirstTransform}
transform {SecondTransform} transform {Translate2} }
T
#end
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 5-2-2024 om 01:11 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
>>> I currently have my nose to the ground, trying to find an algorithm to generate
>>> the inverse of a 9x9 rigid body transform matrix - if I can puzzle that out,
>>> then any object specified with 4 points can be mapped to any other instance with
>>> a transform {matrix{}} statement.
>>> Then I can take one base, look over where it sits somewhere else in the helix,
>>> and calculate exactly how to get it from one place to another.
>>>
>> That could be very useful. Also in a universal sense, applied to all
>> sort of transformations/mutations.
>
> OK, So I haven't ferreted out all the details of the purely matrix approach, but
> while closing one of the 100 browser tabs I have open, I stumbled across a guy
> using Reorient_Trans, and figured that would be a viable approach.
> I had a few false starts due to not really being able to visualize what was
> going on, but after making an IRL model and turning it around a few times, the
> part I was missing / improperly implementing became obvious, and I was able to
> package it all up into a single macro.
>
> Identify any three points on your original object (A, B, C), and where those
> three points end up (A2, B2, C2)
>
> Apply the macro like so:
> #declare MyTransform = Reorient_Triangle (A, B, C, A2, B2, C2)
> object {MyObject transform {MyTransform}}
>
> Please try this out with a large assortment of objects in various orientations
> to see if I missed anything. The only thing not included is a sanity check for
> plugging in a second set of coordinates that are identical to the first.
>
> #macro Reorient_Triangle (A, B, C, A2, B2, C2)
> // Bill Walker "Bald Eagle" February 2024
> #ifndef(TRANSFORMS_INC_TEMP)
> #include "transforms.inc"
> #end
> #local Translate1 = transform {translate -A}
> #local Vector1 = B - A;
> #local Vector2 = B2 - A2;
> // Align Vector1 to Vector2
> #local FirstTransform = transform {Reorient_Trans (Vector1, Vector2)};
> #local A1 = vtransform (A-A, FirstTransform)+A;
> #local B1 = vtransform (B-A, FirstTransform)+A;
> #local C1 = vtransform (C-A, FirstTransform)+A;
> // Find the vector to C1 that is perpendicular to Vector2
> #local T1 = vdot (B1-A1, C1-A1) / vdot (B1-A1, B1-A1);
> #local D = A1 + T1 * (B1-A1);
> #local Vector3 = C1 - D;
> // Find the vector to C2 that is perpendicular to Vector2
> #local T2 = vdot (B2-A2, C2-A2) / vdot (B2-A2, B2-A2);
> #local D2 = A2 + T2 * (B2-A2);
> #local Vector4 = C2 - D2;
> // Rotate everything around Vector2 so that the perpendicular vectors match
> #local SecondTransform = transform {Reorient_Trans (Vector3, Vector4)};
> // Now everything is similarly aligned with 3 sequential transforms
> // and translating a final time puts the object at the destination
> #local Translate2 = transform {translate A2}
> #local T = transform { transform {Translate1} transform {FirstTransform}
> transform {SecondTransform} transform {Translate2} }
>
> T
>
> #end
>
Impressive. I have started to play, first with a complex mesh2 object,
and it works like a charm. I still need to dig deeper obviously, but I
love it.
--
Thomas org> wrote:
>
>>> I currently have my nose to the ground, trying to find an algorithm to generate
>>> the inverse of a 9x9 rigid body transform matrix - if I can puzzle that out,
>>> then any object specified with 4 points can be mapped to any other instance with
>>> a transform {matrix{}} statement.
>>> Then I can take one base, look over where it sits somewhere else in the helix,
>>> and calculate exactly how to get it from one place to another.
>>>
>> That could be very useful. Also in a universal sense, applied to all
>> sort of transformations/mutations.
>
> OK, So I haven't ferreted out all the details of the purely matrix approach, but
> while closing one of the 100 browser tabs I have open, I stumbled across a guy
> using Reorient_Trans, and figured that would be a viable approach.
> I had a few false starts due to not really being able to visualize what was
> going on, but after making an IRL model and turning it around a few times, the
> part I was missing / improperly implementing became obvious, and I was able to
> package it all up into a single macro.
>
> Identify any three points on your original object (A, B, C), and where those
> three points end up (A2, B2, C2)
>
> Apply the macro like so:
> #declare MyTransform = Reorient_Triangle (A, B, C, A2, B2, C2)
> object {MyObject transform {MyTransform}}
>
> Please try this out with a large assortment of objects in various orientations
> to see if I missed anything. The only thing not included is a sanity check for
> plugging in a second set of coordinates that are identical to the first.
>
> #macro Reorient_Triangle (A, B, C, A2, B2, C2)
> // Bill Walker "Bald Eagle" February 2024
> #ifndef(TRANSFORMS_INC_TEMP)
> #include "transforms.inc"
> #end
> #local Translate1 = transform {translate -A}
> #local Vector1 = B - A;
> #local Vector2 = B2 - A2;
> // Align Vector1 to Vector2
> #local FirstTransform = transform {Reorient_Trans (Vector1, Vector2)};
> #local A1 = vtransform (A-A, FirstTransform)+A;
> #local B1 = vtransform (B-A, FirstTransform)+A;
> #local C1 = vtransform (C-A, FirstTransform)+A;
> // Find the vector to C1 that is perpendicular to Vector2
> #local T1 = vdot (B1-A1, C1-A1) / vdot (B1-A1, B1-A1);
> #local D = A1 + T1 * (B1-A1);
> #local Vector3 = C1 - D;
> // Find the vector to C2 that is perpendicular to Vector2
> #local T2 = vdot (B2-A2, C2-A2) / vdot (B2-A2, B2-A2);
> #local D2 = A2 + T2 * (B2-A2);
> #local Vector4 = C2 - D2;
> // Rotate everything around Vector2 so that the perpendicular vectors match
> #local SecondTransform = transform {Reorient_Trans (Vector3, Vector4)};
> // Now everything is similarly aligned with 3 sequential transforms
> // and translating a final time puts the object at the destination
> #local Translate2 = transform {translate A2}
> #local T = transform { transform {Translate1} transform {FirstTransform}
> transform {SecondTransform} transform {Translate2} }
>
> T
>
> #end
>
Impressive. I have started to play, first with a complex mesh2 object,
and it works like a charm. I still need to dig deeper obviously, but I
love it.
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> Impressive. I have started to play, first with a complex mesh2 object,
> and it works like a charm. I still need to dig deeper obviously, but I
> love it.
Thanks Thomas,
I'm glad it's working well for you.
Please try to apply a null/identity transform where the starting points are the
same as the destination points.
I rendered a loop of triangles and they all wound up exactly where they were
supposed to, so I'm hopeful that this is all it will take.
I believe this is what is referred to as a "rigid body transform", as opposed to
an affine transform, which may apply things like scaling or shear.
So I think I just need the ordered triple, which gives us a triangle with a face
normal, and that's all that's necessary and sufficient to completely describe
the orientation.
I'm sure TOK probably coded something like 15 years ago ;)
- BW org> wrote:
> Impressive. I have started to play, first with a complex mesh2 object,
> and it works like a charm. I still need to dig deeper obviously, but I
> love it.
Thanks Thomas,
I'm glad it's working well for you.
Please try to apply a null/identity transform where the starting points are the
same as the destination points.
I rendered a loop of triangles and they all wound up exactly where they were
supposed to, so I'm hopeful that this is all it will take.
I believe this is what is referred to as a "rigid body transform", as opposed to
an affine transform, which may apply things like scaling or shear.
So I think I just need the ordered triple, which gives us a triangle with a face
normal, and that's all that's necessary and sufficient to completely describe
the orientation.
I'm sure TOK probably coded something like 15 years ago ;)
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 07/02/2024 om 01:32 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
>> Impressive. I have started to play, first with a complex mesh2 object,
>> and it works like a charm. I still need to dig deeper obviously, but I
>> love it.
>
> Thanks Thomas,
>
> I'm glad it's working well for you.
> Please try to apply a null/identity transform where the starting points are the
> same as the destination points.
>
> I rendered a loop of triangles and they all wound up exactly where they were
> supposed to, so I'm hopeful that this is all it will take.
>
OK. I shall do that today. There are a couple of questions I am hoarding
at the moment, but that can wait until I have a more complete picture of
the thing.
> I believe this is what is referred to as a "rigid body transform", as opposed to
> an affine transform, which may apply things like scaling or shear.
> So I think I just need the ordered triple, which gives us a triangle with a face
> normal, and that's all that's necessary and sufficient to completely describe
> the orientation.
>
It is smart indeed.
I dimly remembered an old post about Euler matrix rotations:
https://news.povray.org/povray.general/thread/%3Cweb.44d8fc1ca05d1ece40d56c170%40news.povray.org%3E/?ttop=438426&toff=2650
which I almost lost but was hiding in an obscure nook. At the end of the
thread there is a bit of interesting/useful code which seems related to
what you have so smartly cooked up here.
> I'm sure TOK probably coded something like 15 years ago ;)
>
Oh! I am sure he did!
--
Thomas org> wrote:
>
>> Impressive. I have started to play, first with a complex mesh2 object,
>> and it works like a charm. I still need to dig deeper obviously, but I
>> love it.
>
> Thanks Thomas,
>
> I'm glad it's working well for you.
> Please try to apply a null/identity transform where the starting points are the
> same as the destination points.
>
> I rendered a loop of triangles and they all wound up exactly where they were
> supposed to, so I'm hopeful that this is all it will take.
>
OK. I shall do that today. There are a couple of questions I am hoarding
at the moment, but that can wait until I have a more complete picture of
the thing.
> I believe this is what is referred to as a "rigid body transform", as opposed to
> an affine transform, which may apply things like scaling or shear.
> So I think I just need the ordered triple, which gives us a triangle with a face
> normal, and that's all that's necessary and sufficient to completely describe
> the orientation.
>
It is smart indeed.
I dimly remembered an old post about Euler matrix rotations:
https://news.povray.org/povray.general/thread/%3Cweb.44d8fc1ca05d1ece40d56c170%40news.povray.org%3E/?ttop=438426&toff=2650
which I almost lost but was hiding in an obscure nook. At the end of the
thread there is a bit of interesting/useful code which seems related to
what you have so smartly cooked up here.
> I'm sure TOK probably coded something like 15 years ago ;)
>
Oh! I am sure he did!
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> I dimly remembered an old post about Euler matrix rotations:
>
>
https://news.povray.org/povray.general/thread/%3Cweb.44d8fc1ca05d1ece40d56c170%40news.povray.org%3E/?ttop=438426&toff
=2650
>
> which I almost lost but was hiding in an obscure nook. At the end of the
> thread there is a bit of interesting/useful code which seems related to
> what you have so smartly cooked up here.
Very nice. I'll hopefully get a chance to take a look at that code and what it
does in the coming week.
In preparation for that, I wrote a little transform visualization playground
that compares the transformed world coordinates (basis vectors) to the camera
basis vectors.
(I phrase it that way, since if you apply a transform to the camera, you'll get
the effect of transforming all of POV-space with that transform)
It's also difficult for most people to grasp and clearly understand what's going
on with a matrix transform, and keep track of how the basis vectors get
processed, and what the values in the matrix < > (matrix vector) directive
represent.
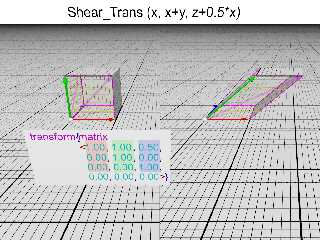
So the first transform I rendered is the Shear_Trans (), since it's a straight
conversion of the basis vector space to what's specified in the matrix vector.
There's really no "shear" unless you specify one.
Shear_Trans () really does nothing except apply a straight transform {matrix
<>}.
You can use it to shear, scale, or rotate, or all 3, depending on what values
you put in for the arguments. You can't do translations with it, since that
last row vector is hard-coded in the macro to 0, 0, 0.
Please hoard those questions and write them all down. The questions we have a
hard time answering are the ones we stand to learn the most from. org> wrote:
> I dimly remembered an old post about Euler matrix rotations:
>
>
https://news.povray.org/povray.general/thread/%3Cweb.44d8fc1ca05d1ece40d56c170%40news.povray.org%3E/?ttop=438426&toff
=2650
>
> which I almost lost but was hiding in an obscure nook. At the end of the
> thread there is a bit of interesting/useful code which seems related to
> what you have so smartly cooked up here.
Very nice. I'll hopefully get a chance to take a look at that code and what it
does in the coming week.
In preparation for that, I wrote a little transform visualization playground
that compares the transformed world coordinates (basis vectors) to the camera
basis vectors.
(I phrase it that way, since if you apply a transform to the camera, you'll get
the effect of transforming all of POV-space with that transform)
It's also difficult for most people to grasp and clearly understand what's going
on with a matrix transform, and keep track of how the basis vectors get
processed, and what the values in the matrix < > (matrix vector) directive
represent.
So the first transform I rendered is the Shear_Trans (), since it's a straight
conversion of the basis vector space to what's specified in the matrix vector.
There's really no "shear" unless you specify one.
Shear_Trans () really does nothing except apply a straight transform {matrix
<>}.
You can use it to shear, scale, or rotate, or all 3, depending on what values
you put in for the arguments. You can't do translations with it, since that
last row vector is hard-coded in the macro to 0, 0, 0.
Please hoard those questions and write them all down. The questions we have a
hard time answering are the ones we stand to learn the most from.
Post a reply to this message
Attachments:
Download 'sheartransform.png' (385 KB)
Preview of image 'sheartransform.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
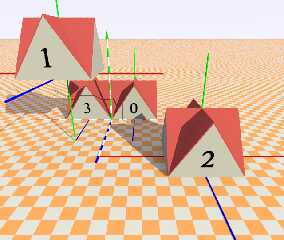
OK. I think I have understood the mechanism, after a couple of wild,
uncontrolled, experiments which were very helpful in the end. A couple
of simple but useful comments:
1) the place of the initial triangle in/on the object is crucial to
understand how the object is going to be moved. The orientation of the
initial triangle is less crucial, although one should keep in mind that
it /might/ become so in some cases.
2) Point 1 is crucial to define/calculate the target triangle. It is
*not* defined from the origin but from the initial triangle.
3) All apices from the triangle have to be translated by an identical
vector value. If not, you may have interesting surprises, mostly
additional rotations to the object. However, those are difficult to
control from the onset if used on purpose.
4) Here follows the code I used to control the macro. The object used is
a prism object that can be found in POV-Ray's Insert Menu. Here it is
declared as 'Roof':
//---------------------------------------------------------------------
#declare Roof =
union {
object {Roof} //the original, inserted, prism object
union {
cylinder {<0,-3,0>,<0,3,0>,0.02 pigment {Green}}
cylinder {<0,-3,0>,<0,3,0>,0.02 pigment {Blue} rotate 90*x}
cylinder {<0,-3,0>,<0,3,0>,0.02 pigment {Red} rotate 90*z}
}
scale <1.00, 1.00, 1.00>*3
rotate <0,0,0>
translate <3.00, 0.00, 3.00>
}
#declare Text0 =
text {
internal 1 "0"
1.0, 0
scale 2
translate <2.5, 1.0, -0.1>
}
#declare Roof0 =
union {
object {Roof}
object {Text0}
}
Roof0
//---------------------------------------------------------------------
//defining the different triangles and translations:
#declare A1 = <0,0,3>;
#declare B1 = <3,4,3>;
#declare C1 = <6,0,3>;
#declare A2 = A1 + <-6,7,-9>;
#declare B2 = B1 + <-6,7,-9>;
#declare C2 = C1 + <-6,7,-9>;
#declare A3 = A2 + <6,0,-12>;
#declare B3 = B2 + <6,0,-12>;
#declare C3 = C2 + <6,0,-12>;
#declare A4 = A3 + <-6,0,0>;
#declare B4 = A3 + <-6,0,0>;
#declare C4 = A3 + <-6,0,0>;
//---------------------------------------------------------------------
#declare MyTransform1 = //A1,B1,C1 -> A2,B2,C2
Reorient_Triangle (
A1, B1, C1,
A2, B2, C2
)
#declare Text1 =
text {
internal 1 "1"
1.0, 0
scale 2
translate <2.5, 1.0, -0.1>
}
#declare Roof1 =
union {
object {Roof}
object {Text1}
}
#declare Roof1 =
object {Roof1 transform {MyTransform1} }
Roof1
//---------------------------------------------------------------------
#declare MyTransform2 = //A2,B2,C2 -> A3,B3,C3
Reorient_Triangle (
A2, B2, C2,
A3, B3, C3
)
#declare Text2 =
text {
internal 1 "2"
1.0, 0
scale 2
translate <2.5, 1.0, -0.1>
}
#declare Roof2 =
union {
object {Roof}
object {Text2}
}
#declare Roof2 =
object {Roof2 transform {MyTransform2} }
Roof2
//---------------------------------------------------------------------
#declare MyTransform3 = //A3,B3,C3 -> A4,B4,C4
Reorient_Triangle (
A3, B3, C3,
A4, B4, C4
)
#declare Text3 =
text {
internal 1 "3"
1.0, 0
scale 2
translate <2.5, 1.0, -0.1>
}
#declare Roof3 =
union {
object {Roof}
object {Text3}
}
#declare Roof3 =
object {Roof3 transform {MyTransform3} }
Roof3
//---------------------------------------------------------------------
--
Thomas
Post a reply to this message
Attachments:
Download 'be_reorient_triangle_test.png' (331 KB)
Preview of image 'be_reorient_triangle_test.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> 2) Point 1 is crucial to define/calculate the target triangle. It is
> *not* defined from the origin but from the initial triangle.
>
> 3) All apices from the triangle have to be translated by an identical
> vector value. If not, you may have interesting surprises, mostly
> additional rotations to the object. However, those are difficult to
> control from the onset if used on purpose.
Right. The macro takes your exact triangle, and moves it from right where it
is, to exactly where it would be if you moved it there with some unknown
combinations of rotations and translations.
I did wonder what would happen if I jimmied some of the target triangle
coordinates, and yes, the triangles got moved - but I have yet to quantify
exactly how.
- BW org> wrote:
> 2) Point 1 is crucial to define/calculate the target triangle. It is
> *not* defined from the origin but from the initial triangle.
>
> 3) All apices from the triangle have to be translated by an identical
> vector value. If not, you may have interesting surprises, mostly
> additional rotations to the object. However, those are difficult to
> control from the onset if used on purpose.
Right. The macro takes your exact triangle, and moves it from right where it
is, to exactly where it would be if you moved it there with some unknown
combinations of rotations and translations.
I did wonder what would happen if I jimmied some of the target triangle
coordinates, and yes, the triangles got moved - but I have yet to quantify
exactly how.
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()