 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> No worry, Bill. As you know, we like to poke into the hot coals once in
> a while. Life (the Real one) has its own pace and priorities, I know all
> too well... Take care and don't get overwhelmed.
Here's a hot coal in yer eye... ;)
> Also avoid batch 22-0004-b043 of your Dried Frog Pills, if you still
> have it. It has been contaminated with jitter powder from an unknown
> source. :-)
Oh. NOW you tell me. I thought they were fruit flies or fungus gnats, or
floaties. Or the usual bits of dust or smudge on my monitor.
The antispasmodic quinine in my G&T's seem to help with the other jitters. :P
I think this addresses the basic grid-based Voronoi, in an infinite tiling.
As usual, I was making it 10,000 times more difficult than it should be.
Shown is the pattern on the xz plane, with the unit square from 0 to 1 outlined
in magenta.
I'm using f_noise3d as my randomization function, but I'm not quite sure how to
get it "to be more random" using my <x,y,z> coordinates.
I'd also like to find a way to modify the output values of the Voronoi function
to give something more like crackle solid, or at least a hard outline of the
cells.
I think I can modify this so that the points are user-defined, but the pattern
still tiles. org> wrote:
> No worry, Bill. As you know, we like to poke into the hot coals once in
> a while. Life (the Real one) has its own pace and priorities, I know all
> too well... Take care and don't get overwhelmed.
Here's a hot coal in yer eye... ;)
> Also avoid batch 22-0004-b043 of your Dried Frog Pills, if you still
> have it. It has been contaminated with jitter powder from an unknown
> source. :-)
Oh. NOW you tell me. I thought they were fruit flies or fungus gnats, or
floaties. Or the usual bits of dust or smudge on my monitor.
The antispasmodic quinine in my G&T's seem to help with the other jitters. :P
I think this addresses the basic grid-based Voronoi, in an infinite tiling.
As usual, I was making it 10,000 times more difficult than it should be.
Shown is the pattern on the xz plane, with the unit square from 0 to 1 outlined
in magenta.
I'm using f_noise3d as my randomization function, but I'm not quite sure how to
get it "to be more random" using my <x,y,z> coordinates.
I'd also like to find a way to modify the output values of the Voronoi function
to give something more like crackle solid, or at least a hard outline of the
cells.
I think I can modify this so that the points are user-defined, but the pattern
still tiles.
Post a reply to this message
Attachments:
Download 'tileablevoronoitest.png' (160 KB)
Preview of image 'tileablevoronoitest.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 1-12-2022 om 00:29 schreef Bald Eagle:
> I think this addresses the basic grid-based Voronoi, in an infinite tiling.
>
> As usual, I was making it 10,000 times more difficult than it should be.
>
> Shown is the pattern on the xz plane, with the unit square from 0 to 1 outlined
> in magenta.
>
> I'm using f_noise3d as my randomization function, but I'm not quite sure how to
> get it "to be more random" using my <x,y,z> coordinates.
>
> I'd also like to find a way to modify the output values of the Voronoi function
> to give something more like crackle solid, or at least a hard outline of the
> cells.
>
> I think I can modify this so that the points are user-defined, but the pattern
> still tiles.
>
This looks very promising indeed. Well done!
Would it be possible to vary the /size/ of the individual cells? in a
random way?
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> This looks very promising indeed. Well done!
>
> Would it be possible to vary the /size/ of the individual cells? in a
> random way?
Certainly.
The size of the cells is determined by the proximity of the vertices/centers.
So rather than arranging the points in a grid with some randomness, I can just
sprinkle points into the unit square at random. at this point, I don't think
there's a whole lot that's out of the realm of possibility.
I need to go out and run some errands, and then hopefully later I'll have some
time to modify the current scene.
I also coded up some special hocus-pocus that may allow for a true
function-based full color Voronoi pattern, and maybe even the full color crackle
solid. I have code that runs without errors, but it doesn't do what I want -
though I suspect why and have a plan for how to investigate and debug. It's
also remarkably slow, for some unknown reason, as I'm not daisy-chaining 100+
functions together like my initial attempts. So, "technical difficulties" as
always.
- BE org> wrote:
> This looks very promising indeed. Well done!
>
> Would it be possible to vary the /size/ of the individual cells? in a
> random way?
Certainly.
The size of the cells is determined by the proximity of the vertices/centers.
So rather than arranging the points in a grid with some randomness, I can just
sprinkle points into the unit square at random. at this point, I don't think
there's a whole lot that's out of the realm of possibility.
I need to go out and run some errands, and then hopefully later I'll have some
time to modify the current scene.
I also coded up some special hocus-pocus that may allow for a true
function-based full color Voronoi pattern, and maybe even the full color crackle
solid. I have code that runs without errors, but it doesn't do what I want -
though I suspect why and have a plan for how to investigate and debug. It's
also remarkably slow, for some unknown reason, as I'm not daisy-chaining 100+
functions together like my initial attempts. So, "technical difficulties" as
always.
- BE
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I also coded up some special hocus-pocus that may allow for a true
> function-based full color Voronoi pattern, and maybe even the full color crackle
> solid. I have code that runs without errors, but it doesn't do what I want -
> though I suspect why and have a plan for how to investigate and debug. It's
> also remarkably slow, for some unknown reason, as I'm not daisy-chaining 100+
> functions together like my initial attempts. So, "technical difficulties" as
> always.
Got back in late-ish and I needed to clarify a few things on the color code, so
no random set yet - tonight, for sure, since it's such a fast thing to do.
But I did get a clearer picture of what I was doing, and where and how it was
going wrong.
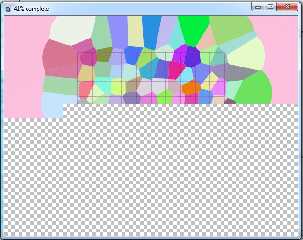
It SLOW, and therefore I'm posting a rendering-as-we-speak screenshot. But is
undeniably a full color solid Voronoi pattern, and it done entire in SDL and
only with functions, since the only object in the scene is
plane {y, -D texture {RGBPigment}}
I need to fix the parts that will make the coloring tile along with the pattern,
(I did this before First Coffee) but aside from that, this is proof of concept.
Now someone, maybe Thorsten, can investigate WHY this version is so slow,
whereas the grayscale version is tolerably fast. I'm only at 50% rendered at 38
min, for a 640 x 480 image. :( net> wrote:
> I also coded up some special hocus-pocus that may allow for a true
> function-based full color Voronoi pattern, and maybe even the full color crackle
> solid. I have code that runs without errors, but it doesn't do what I want -
> though I suspect why and have a plan for how to investigate and debug. It's
> also remarkably slow, for some unknown reason, as I'm not daisy-chaining 100+
> functions together like my initial attempts. So, "technical difficulties" as
> always.
Got back in late-ish and I needed to clarify a few things on the color code, so
no random set yet - tonight, for sure, since it's such a fast thing to do.
But I did get a clearer picture of what I was doing, and where and how it was
going wrong.
It SLOW, and therefore I'm posting a rendering-as-we-speak screenshot. But is
undeniably a full color solid Voronoi pattern, and it done entire in SDL and
only with functions, since the only object in the scene is
plane {y, -D texture {RGBPigment}}
I need to fix the parts that will make the coloring tile along with the pattern,
(I did this before First Coffee) but aside from that, this is proof of concept.
Now someone, maybe Thorsten, can investigate WHY this version is so slow,
whereas the grayscale version is tolerably fast. I'm only at 50% rendered at 38
min, for a 640 x 480 image. :(
Post a reply to this message
Attachments:
Download 'fullcolortilablevoronoi.jpg' (253 KB)
Preview of image 'fullcolortilablevoronoi.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Good progress, though!
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> It SLOW, and therefore I'm posting a rendering-as-we-speak screenshot. But is
> undeniably a full color solid Voronoi pattern, and it done entire in SDL and
> only with functions, since the only object in the scene is
>
> plane {y, -D texture {RGBPigment}}
So I'm curious to know what you've done here - are you aiming for simply a
tileable version of the crackle pattern? Can this also be colored on a per-cell
basis like my object-based version, or is it just the tiling you're after?
I'd love to see the code once it's in a fit state :)
Bill net> wrote:
> It SLOW, and therefore I'm posting a rendering-as-we-speak screenshot. But is
> undeniably a full color solid Voronoi pattern, and it done entire in SDL and
> only with functions, since the only object in the scene is
>
> plane {y, -D texture {RGBPigment}}
So I'm curious to know what you've done here - are you aiming for simply a
tileable version of the crackle pattern? Can this also be colored on a per-cell
basis like my object-based version, or is it just the tiling you're after?
I'd love to see the code once it's in a fit state :)
Bill
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 02/12/2022 13:17, Bald Eagle wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:> ...
> plane {y, -D texture {RGBPigment}}
> ...
>
This kind of code is a very big mystery to me :(
T-O-K also uses it a lot in his code about complex functions.
I had also played a bit with the Voroni diagrams. The statistics for the
attached image are :
----------------------------------------------------------------------------
Parser Time
Parse Time: 0 hours 0 minutes 28 seconds (28.481 seconds)
using 1 thread(s) with 28.477 CPU-seconds total
Bounding Time: 0 hours 0 minutes 0 seconds (0.205 seconds)
using 1 thread(s) with 0.205 CPU-seconds total
----------------------------------------------------------------------------
Render Time:
Photon Time: No photons
Radiosity Time: No radiosity
Trace Time: 0 hours 0 minutes 1 seconds (1.575 seconds)
using 6 thread(s) with 5.942 CPU-seconds total
----------------------------------------------------------------------------
... about 30" for 400x400 "points".
The method for the plot is very very basic (even silly).
I can give the SDL of corse
It's strange from you ...
Is your code recursif ?
--
Kurtz le pirate
Compagnie de la Banquise net> wrote:> ...
> plane {y, -D texture {RGBPigment}}
> ...
>
This kind of code is a very big mystery to me :(
T-O-K also uses it a lot in his code about complex functions.
I had also played a bit with the Voroni diagrams. The statistics for the
attached image are :
----------------------------------------------------------------------------
Parser Time
Parse Time: 0 hours 0 minutes 28 seconds (28.481 seconds)
using 1 thread(s) with 28.477 CPU-seconds total
Bounding Time: 0 hours 0 minutes 0 seconds (0.205 seconds)
using 1 thread(s) with 0.205 CPU-seconds total
----------------------------------------------------------------------------
Render Time:
Photon Time: No photons
Radiosity Time: No radiosity
Trace Time: 0 hours 0 minutes 1 seconds (1.575 seconds)
using 6 thread(s) with 5.942 CPU-seconds total
----------------------------------------------------------------------------
... about 30" for 400x400 "points".
The method for the plot is very very basic (even silly).
I can give the SDL of corse
It's strange from you ...
Is your code recursif ?
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
Attachments:
Download 'voro_basic.jpg' (25 KB)
Preview of image 'voro_basic.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bill Pragnell" <bil### [at] hotmail com> wrote:
> So I'm curious to know what you've done here - are you aiming for simply a
> tileable version of the crackle pattern? Can this also be colored on a per-cell
> basis like my object-based version, or is it just the tiling you're after?
>
> I'd love to see the code once it's in a fit state :)
1. The original, long-standing, and long-desired, and often requested goal was
to have a user-defined set of cell vertices.
2. My personal long-standing goal was to understand how to create a Voronoi
pattern from scratch.
3. I have demonstrated that tileable Voronoi is possible, and of course, native
built-in POV-Ray tileable crackle {} is supported, but easily made even if it
wasn't.
4. What you're currently looking at is a full, user-defined cell vertice
Voronoi pattern, that is infinitely tileable, and able to be colored on a
per-cell basis by a user-defined array.
Tdg and jr have commented that "the math" behind this is a mystery, and beyond
them. Not so, as "the math", what little there is, is minimal, and well within
their grasp, as most of it is, or can be, handled by POV-Ray.
I was very pleased with my long-overdue understanding of how to generate a
Voronoi pattern from first principles. You and I agreed that the scalar output
of the function would "scrub" any information about the underlying cells, which
it does.
But as I was working the tiled version, the truth of the matter finally made
it's way through to me, and the solution is what I am calling POV-Ray CHEMistry.
The Coding-Human-Elementary Math interplay.
The Voronoi pattern is a "semiprocedural" pattern generated int he following
way:
You define the cell vertex points. [A, B, C, ....]
You calculate the distance between the current pixel (P) and each vertex point.
This amounts to vlength (A-P)
Then you just use a #for loop to shove all the distance calculations into a min
() statement to find the shortest distance / closest point.
You can use a select () function to limit the "reach" of this if you want...
So the output of the Voronoi function is a scalar distance.
It has no memory of where this number came from, and the math does not give us
any additional information.
But we are not limited to math, are we?
We are humans, and capable of recognizing patterns and properties, and reasoning
outside of the math.
And this is where are able to write the code to get the coordinates of the cell
vertex that generated the distance.
Pick any point in any of the Voronoi cells, and what do we know about it?
We know that that point is closer to that cell's vertex than any other cell
vertex - because this is the definition of the pattern. So if I now (again)
calculate the distance between that pixel and every cell vertex, it will only
match a single Voronoi result in the original function.
How do we apply this Human understanding to the math and the code?
We compare the distance between the current pixel and each cell vertex to see if
they are equal.
This easily done by subtracting one from the other, since if they are equal,
then the result is zero.
So we can plug this into a select () statement, and if Distance-Voronoi is zero,
then --- return the Spline Index value for that vertex, otherwise, zero.
But we need to do this for ALL of the cell vertices, and so all we do is once
again use a #for loop to shove all those calculations into a sum () function.
All of the vertices that _aren't_ the closest one sum to zero, but the closest
one adds its Spline Index value to the result.
Now, we can define a parallel spline function that indexes RGB color values
instead of cell vertices.
And, instead of coloring the pixel based upon the grayscale value of the
distance function, we can just use the RGB value that the user assigns to that
cell vertex to color _every_ pixel that is closest to that cell vertex.
And there you go - full color, solid Voronoi, from SDL-only scalar-only POV-Ray
functions.
We can then use the distance function to multiply the rgb value to get colored
shading, and the index value to define other arrays for textures, finishes,
normals, etc.
To make this tile infinitely, we just restrict the vertices to the 0-1 range,
and use select () and abs () to make mod() behave nicely across the -, 0, +
transition.
I'll hopefully clean up some of the code this weekend, and add a full discussion
of this as a section to my Function Monograph that I started writing for folks
like Kenneth.
I'll have to take a look at why it's SO SLOW. But other than that, I'd say
that future development would include a weighted Voronoi (which may be analogous
to POV-Ray's crackle form vector), a 3D version / expansion of the current
implementation, and also figuring out the best way to implement the Delaunay
triangulation - either from first principles, or by using the Voronoi as a
basis.
I'm thinking that a 3-pass Voronoi pattern would give the 3 closest cell
vertices, and then I can use triangle {} to show the pattern.
Also, maybe we can apply this POV-Ray CHEMistry to some past problems or new
projects to see how far we can push it. com> wrote:
> So I'm curious to know what you've done here - are you aiming for simply a
> tileable version of the crackle pattern? Can this also be colored on a per-cell
> basis like my object-based version, or is it just the tiling you're after?
>
> I'd love to see the code once it's in a fit state :)
1. The original, long-standing, and long-desired, and often requested goal was
to have a user-defined set of cell vertices.
2. My personal long-standing goal was to understand how to create a Voronoi
pattern from scratch.
3. I have demonstrated that tileable Voronoi is possible, and of course, native
built-in POV-Ray tileable crackle {} is supported, but easily made even if it
wasn't.
4. What you're currently looking at is a full, user-defined cell vertice
Voronoi pattern, that is infinitely tileable, and able to be colored on a
per-cell basis by a user-defined array.
Tdg and jr have commented that "the math" behind this is a mystery, and beyond
them. Not so, as "the math", what little there is, is minimal, and well within
their grasp, as most of it is, or can be, handled by POV-Ray.
I was very pleased with my long-overdue understanding of how to generate a
Voronoi pattern from first principles. You and I agreed that the scalar output
of the function would "scrub" any information about the underlying cells, which
it does.
But as I was working the tiled version, the truth of the matter finally made
it's way through to me, and the solution is what I am calling POV-Ray CHEMistry.
The Coding-Human-Elementary Math interplay.
The Voronoi pattern is a "semiprocedural" pattern generated int he following
way:
You define the cell vertex points. [A, B, C, ....]
You calculate the distance between the current pixel (P) and each vertex point.
This amounts to vlength (A-P)
Then you just use a #for loop to shove all the distance calculations into a min
() statement to find the shortest distance / closest point.
You can use a select () function to limit the "reach" of this if you want...
So the output of the Voronoi function is a scalar distance.
It has no memory of where this number came from, and the math does not give us
any additional information.
But we are not limited to math, are we?
We are humans, and capable of recognizing patterns and properties, and reasoning
outside of the math.
And this is where are able to write the code to get the coordinates of the cell
vertex that generated the distance.
Pick any point in any of the Voronoi cells, and what do we know about it?
We know that that point is closer to that cell's vertex than any other cell
vertex - because this is the definition of the pattern. So if I now (again)
calculate the distance between that pixel and every cell vertex, it will only
match a single Voronoi result in the original function.
How do we apply this Human understanding to the math and the code?
We compare the distance between the current pixel and each cell vertex to see if
they are equal.
This easily done by subtracting one from the other, since if they are equal,
then the result is zero.
So we can plug this into a select () statement, and if Distance-Voronoi is zero,
then --- return the Spline Index value for that vertex, otherwise, zero.
But we need to do this for ALL of the cell vertices, and so all we do is once
again use a #for loop to shove all those calculations into a sum () function.
All of the vertices that _aren't_ the closest one sum to zero, but the closest
one adds its Spline Index value to the result.
Now, we can define a parallel spline function that indexes RGB color values
instead of cell vertices.
And, instead of coloring the pixel based upon the grayscale value of the
distance function, we can just use the RGB value that the user assigns to that
cell vertex to color _every_ pixel that is closest to that cell vertex.
And there you go - full color, solid Voronoi, from SDL-only scalar-only POV-Ray
functions.
We can then use the distance function to multiply the rgb value to get colored
shading, and the index value to define other arrays for textures, finishes,
normals, etc.
To make this tile infinitely, we just restrict the vertices to the 0-1 range,
and use select () and abs () to make mod() behave nicely across the -, 0, +
transition.
I'll hopefully clean up some of the code this weekend, and add a full discussion
of this as a section to my Function Monograph that I started writing for folks
like Kenneth.
I'll have to take a look at why it's SO SLOW. But other than that, I'd say
that future development would include a weighted Voronoi (which may be analogous
to POV-Ray's crackle form vector), a 3D version / expansion of the current
implementation, and also figuring out the best way to implement the Delaunay
triangulation - either from first principles, or by using the Voronoi as a
basis.
I'm thinking that a 3-pass Voronoi pattern would give the 3 closest cell
vertices, and then I can use triangle {} to show the pattern.
Also, maybe we can apply this POV-Ray CHEMistry to some past problems or new
projects to see how far we can push it.
Post a reply to this message
Attachments:
Download 'tileablevoronoitest.png' (96 KB)
Preview of image 'tileablevoronoitest.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
> This kind of code is a very big mystery to me :(
> T-O-K also uses it a lot in his code about complex functions.
It doesn't need to be, and once you understand the basics of how it works, it's
a very powerful technique that you can use a wide variety of purposes.
You can get a simple idea of how it all works by defining a simple distance
function to any pixel. vlength (x, y, z) is the Euclidian distance to any
pixel from the origin.
So just do:
#declare Distance = function {vlength (x, y, z)}
and then do
plane {z, 0 pigment {function {Distance (x, y, z}}
> It's strange from you ...
> Is your code recursif ?
It's not - it's a few simple functions that are just layered together. I just
wrote a description of how it all works. com> wrote:
> This kind of code is a very big mystery to me :(
> T-O-K also uses it a lot in his code about complex functions.
It doesn't need to be, and once you understand the basics of how it works, it's
a very powerful technique that you can use a wide variety of purposes.
You can get a simple idea of how it all works by defining a simple distance
function to any pixel. vlength (x, y, z) is the Euclidian distance to any
pixel from the origin.
So just do:
#declare Distance = function {vlength (x, y, z)}
and then do
plane {z, 0 pigment {function {Distance (x, y, z}}
> It's strange from you ...
> Is your code recursif ?
It's not - it's a few simple functions that are just layered together. I just
wrote a description of how it all works.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 02/12/2022 21:48, Bald Eagle wrote:
> kurtz le pirate <kur### [at] gmail com> wrote:
>
>> This kind of code is a very big mystery to me :(
>> T-O-K also uses it a lot in his code about complex functions.
>
> It doesn't need to be, and once you understand the basics of how it works, it's
> a very powerful technique that you can use a wide variety of purposes.
>
> You can get a simple idea of how it all works by defining a simple distance
> function to any pixel. vlength (x, y, z) is the Euclidian distance to any
> pixel from the origin.
>
> So just do:
>
> #declare Distance = function {vlength (x, y, z)}
> and then do
>
> plane {z, 0 pigment {function {Distance (x, y, z}}
>
LOL !
2.2.1.6 User-Defined Functions
...Excluded are for example strlen or vlength...
and thank you for this little example that sheds a little
light on my lantern
--
Kurtz le pirate
Compagnie de la Banquise com> wrote:
>
>> This kind of code is a very big mystery to me :(
>> T-O-K also uses it a lot in his code about complex functions.
>
> It doesn't need to be, and once you understand the basics of how it works, it's
> a very powerful technique that you can use a wide variety of purposes.
>
> You can get a simple idea of how it all works by defining a simple distance
> function to any pixel. vlength (x, y, z) is the Euclidian distance to any
> pixel from the origin.
>
> So just do:
>
> #declare Distance = function {vlength (x, y, z)}
> and then do
>
> plane {z, 0 pigment {function {Distance (x, y, z}}
>
LOL !
2.2.1.6 User-Defined Functions
...Excluded are for example strlen or vlength...
and thank you for this little example that sheds a little
light on my lantern
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()