 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
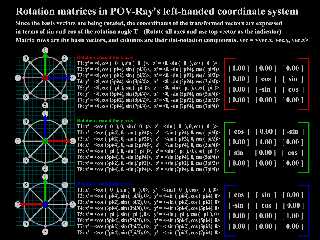
I had the unexpected "opportunity" to review some old code I've had on the
back-burner as a refresher and to look for any errors, and I spotted some errors
in some of the matrix transforms I was using to create some vectors.
Since we use a left-handed coordinate system, and rotation matrices can be a bit
confusing - especially at first - I made a sketch, and then decided it ought to
be added to the collection of documentation diagrams I'm making.
There may be some additional graphics on this specific topics if I find the time
amidst all the other stuff.
As far as I can tell there was no explicit mention of using the formulas of the
transformed basis vectors in isosurface variable substitution on either Mike
Williams' site or Friedrich Lohmueller's. Though they do appear in POV-Ray's
online documentation.
http://www.povray.org/documentation/view/3.7.1/73/
Rotate
Note: these rotation substitutions work like normal POV-rotations: they already
compensate for the inverse working
rotate around X
: replace "y" with "z*sin(radians(Angle)) + y*cos(radians(Angle))"
: replace "z" with "z*cos(radians(Angle)) - y*sin(radians(Angle))"
rotate around Y
: replace "x" with "x*cos(radians(Angle)) - z*sin(radians(Angle))"
: replace "z" with "x*sin(radians(Angle)) + z*cos(radians(Angle))"
rotate around Z
: replace "x" with "x*cos(radians(Angle)) + y*sin(radians(Angle))"
: replace "y" with "-x*sin(radians(Angle)) + y*cos(radians(Angle)) "
rotate z*75 gives:
P(x*cos(radians(75)) + y*sin(radians(75)),
-x*sin(radians(75)) + y*cos(radians(75)), z)
Anyway,
Here is a supplementary illustration - it could probably use some polishing.
Post a reply to this message
Attachments:
Download 'rotationmatrices.png' (296 KB)
Preview of image 'rotationmatrices.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Since we use a left-handed coordinate system, and rotation matrices can be a bit
> confusing - especially at first - I made a sketch, and then decided it ought to
> be added to the collection of documentation diagrams I'm making.
>...
> Here is a supplementary illustration - it could probably use some polishing.
Nice illustration.
To improve it I suggest that you remove the decimals. This will give you some
more space and make it easier to read.
I also suggest that you insert a note to the reader that POV-Ray's trigonometric
functions use radians, not degrees as in you basis vector lists.
Further; some of the equal signs have become minus signs. Could this be caused
by some scaling of the image ?
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
> Since we use a left-handed coordinate system, and rotation matrices can be a bit
> confusing - especially at first - I made a sketch, and then decided it ought to
> be added to the collection of documentation diagrams I'm making.
>...
> Here is a supplementary illustration - it could probably use some polishing.
Nice illustration.
To improve it I suggest that you remove the decimals. This will give you some
more space and make it easier to read.
I also suggest that you insert a note to the reader that POV-Ray's trigonometric
functions use radians, not degrees as in you basis vector lists.
Further; some of the equal signs have become minus signs. Could this be caused
by some scaling of the image ?
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> Nice illustration.
Thank you, Sir.
> To improve it I suggest that you remove the decimals. This will give you some
> more space and make it easier to read.
Yes, I was waffling on that - too many, too few... hard to judge.
It's always tough to try to squeeze a lot of information into a limited space.
There's a weird 3-fold aspect to the way the vectors are represented in the
matrices that I'm trying to capture, but unsure what the best way to go about it
is. Each row is an x, y, z basis vector. Each column of that row is an x, y,
z vector component. And then the final transform is the "sumproduct" for all of
the columns - the x' vector is x.x + y.x + z.x + w.x
So I left all of that criss-crossing out for now. ;)
> I also suggest that you insert a note to the reader that POV-Ray's trigonometric
> functions use radians, not degrees as in you[r] basis vector lists.
I will keep that in mind. I have one or two other "documentation illustrations"
in mind. I would also like to figure out if there's a nice
degrees-to-fractions-of-pi algorithm out there, and I could implement that.
I'll probably just hard-code an array of text objects.
> Further; some of the equal signs have become minus signs. Could this be caused
> by some scaling of the image ?
IIRC, it's an antialiasing thing. I noticed it, but let it slide, hoping for
more feedback before I revised the entire thing. Maybe I'll see if I can find
a bold font to replace 'timrom' with.
Or maybe I'll just scale the font in the y-direction a little bit to thicken the
horizontal lines.
Do you watch 3blue1brown's channel? It's - peaceful, and elegant, and
mesmerizing. It's one of the best things to happen to math in a long while.
:) com> wrote:
> Nice illustration.
Thank you, Sir.
> To improve it I suggest that you remove the decimals. This will give you some
> more space and make it easier to read.
Yes, I was waffling on that - too many, too few... hard to judge.
It's always tough to try to squeeze a lot of information into a limited space.
There's a weird 3-fold aspect to the way the vectors are represented in the
matrices that I'm trying to capture, but unsure what the best way to go about it
is. Each row is an x, y, z basis vector. Each column of that row is an x, y,
z vector component. And then the final transform is the "sumproduct" for all of
the columns - the x' vector is x.x + y.x + z.x + w.x
So I left all of that criss-crossing out for now. ;)
> I also suggest that you insert a note to the reader that POV-Ray's trigonometric
> functions use radians, not degrees as in you[r] basis vector lists.
I will keep that in mind. I have one or two other "documentation illustrations"
in mind. I would also like to figure out if there's a nice
degrees-to-fractions-of-pi algorithm out there, and I could implement that.
I'll probably just hard-code an array of text objects.
> Further; some of the equal signs have become minus signs. Could this be caused
> by some scaling of the image ?
IIRC, it's an antialiasing thing. I noticed it, but let it slide, hoping for
more feedback before I revised the entire thing. Maybe I'll see if I can find
a bold font to replace 'timrom' with.
Or maybe I'll just scale the font in the y-direction a little bit to thicken the
horizontal lines.
Do you watch 3blue1brown's channel? It's - peaceful, and elegant, and
mesmerizing. It's one of the best things to happen to math in a long while.
:)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 05/04/2021 om 02:05 schreef Bald Eagle:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>> Further; some of the equal signs have become minus signs. Could this be caused
>> by some scaling of the image ?
>
> IIRC, it's an antialiasing thing. I noticed it, but let it slide, hoping for
> more feedback before I revised the entire thing. Maybe I'll see if I can find
> a bold font to replace 'timrom' with.
> Or maybe I'll just scale the font in the y-direction a little bit to thicken the
> horizontal lines.
>
or use stochastic aa. That would solve the problem in an elegant way.
Nice work, sir. Very useful indeed.
--
Thomas com> wrote:
>> Further; some of the equal signs have become minus signs. Could this be caused
>> by some scaling of the image ?
>
> IIRC, it's an antialiasing thing. I noticed it, but let it slide, hoping for
> more feedback before I revised the entire thing. Maybe I'll see if I can find
> a bold font to replace 'timrom' with.
> Or maybe I'll just scale the font in the y-direction a little bit to thicken the
> horizontal lines.
>
or use stochastic aa. That would solve the problem in an elegant way.
Nice work, sir. Very useful indeed.
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> or use stochastic aa. That would solve the problem in an elegant way.
You've gotta school me in that black art. Although I have delved deeply into
some of the more esoteric areas of POV-Ray, through neglect, I still have the
lowest level of understanding with regard to the antialiasing settings.
is that the +ua or the +am3, or another one... ? org> wrote:
> or use stochastic aa. That would solve the problem in an elegant way.
You've gotta school me in that black art. Although I have delved deeply into
some of the more esoteric areas of POV-Ray, through neglect, I still have the
lowest level of understanding with regard to the antialiasing settings.
is that the +ua or the +am3, or another one... ?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 5-4-2021 om 13:08 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
>> or use stochastic aa. That would solve the problem in an elegant way.
>
> You've gotta school me in that black art. Although I have delved deeply into
> some of the more esoteric areas of POV-Ray, through neglect, I still have the
> lowest level of understanding with regard to the antialiasing settings.
>
> is that the +ua or the +am3, or another one... ?
>
>
I currently use:
// +am3 +a0.01 +ac0.90 +r3
Which gives me good results. Higher settings, but slower, would be:
// +am3 +a0.001 +ac0.99 +r4
And faster, but uglier, good for testing, something like:
// +am3 +a0.1 +ac0.80 +r2
--
Thomas org> wrote:
>
>> or use stochastic aa. That would solve the problem in an elegant way.
>
> You've gotta school me in that black art. Although I have delved deeply into
> some of the more esoteric areas of POV-Ray, through neglect, I still have the
> lowest level of understanding with regard to the antialiasing settings.
>
> is that the +ua or the +am3, or another one... ?
>
>
I currently use:
// +am3 +a0.01 +ac0.90 +r3
Which gives me good results. Higher settings, but slower, would be:
// +am3 +a0.001 +ac0.99 +r4
And faster, but uglier, good for testing, something like:
// +am3 +a0.1 +ac0.80 +r2
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> // +am3 +a0.001 +ac0.99 +r4
I tried that, but even that wasn't good enough to make the "=" fully visible.
scaling along y by 1.2 improved matters, but then I just switched over to Times
New Roman Bold and kept the scaling as well.
Changed the angles to radians.
Slight color changes on the tori.
I didn't feel like going full utf8 to get a proper pi character - yet. org> wrote:
> // +am3 +a0.001 +ac0.99 +r4
I tried that, but even that wasn't good enough to make the "=" fully visible.
scaling along y by 1.2 improved matters, but then I just switched over to Times
New Roman Bold and kept the scaling as well.
Changed the angles to radians.
Slight color changes on the tori.
I didn't feel like going full utf8 to get a proper pi character - yet.
Post a reply to this message
Attachments:
Download 'rotationmatrices.png' (416 KB)
Preview of image 'rotationmatrices.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 05/04/2021 om 22:53 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
>> // +am3 +a0.001 +ac0.99 +r4
>
> I tried that, but even that wasn't good enough to make the "=" fully visible.
>
> scaling along y by 1.2 improved matters, but then I just switched over to Times
> New Roman Bold and kept the scaling as well.
> Changed the angles to radians.
> Slight color changes on the tori.
>
> I didn't feel like going full utf8 to get a proper pi character - yet.
>
It is the results that count. :-)
--
Thomas org> wrote:
>
>> // +am3 +a0.001 +ac0.99 +r4
>
> I tried that, but even that wasn't good enough to make the "=" fully visible.
>
> scaling along y by 1.2 improved matters, but then I just switched over to Times
> New Roman Bold and kept the scaling as well.
> Changed the angles to radians.
> Slight color changes on the tori.
>
> I didn't feel like going full utf8 to get a proper pi character - yet.
>
It is the results that count. :-)
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail net> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>
> > I also suggest that you insert a note to the reader that POV-Ray's
> > trigonometric functions use radians, not degrees as in you[r] basis
> > vector lists.
>
> I will keep that in mind. I have one or two other "documentation illustrations"
> in mind.
I usually like to use trig functions in degrees rather than radians-- just
easier to visualize for me. "math.inc" has some simple little 'converter'
functions, sind() and cosd()
So in your diagram, for example...
T5: y'= <0,cosd(180), sind(180>
But for your matrix illustrations, I don't know if they should be used (since I
don't know enough about matrix math).
like, -sind instead of -sin ?? com> wrote:
>
> > I also suggest that you insert a note to the reader that POV-Ray's
> > trigonometric functions use radians, not degrees as in you[r] basis
> > vector lists.
>
> I will keep that in mind. I have one or two other "documentation illustrations"
> in mind.
I usually like to use trig functions in degrees rather than radians-- just
easier to visualize for me. "math.inc" has some simple little 'converter'
functions, sind() and cosd()
So in your diagram, for example...
T5: y'= <0,cosd(180), sind(180>
But for your matrix illustrations, I don't know if they should be used (since I
don't know enough about matrix math).
like, -sind instead of -sin ??
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Kenneth" <kdw### [at] gmail com> wrote:
> I usually like to use trig functions in degrees rather than radians-- just
> easier to visualize for me. "math.inc" has some simple little 'converter'
> functions, sind() and cosd()
I was playing around with some things the other day, writing my function
document, and noticed that we don't need "math.inc" anymore - at least not in
3.8. :)
> But for your matrix illustrations, I don't know if they should be used (since I
> don't know enough about matrix math).
I just put sin and cos because everyone everywhere knows what that is and I
would hope that most people would assume that it's implied that there's a
degrees - to - radians conversion... But "matrix math" is no different than
"spreadsheet math" or pencil and paper math or chalkboard math.... it's just a
way of laying things out so that the values in the places are operated on by the
appropriate values in the places of other matrices. Or that the formulas for
things like determinants are using the right values. No magic.
It's just an organizational thing to make the notation compact.
Just think about it as: array {Vec.x, Vec.y, Vec.z} and then make a 2D array
with 2 or 3 more vectors.... com> wrote:
> I usually like to use trig functions in degrees rather than radians-- just
> easier to visualize for me. "math.inc" has some simple little 'converter'
> functions, sind() and cosd()
I was playing around with some things the other day, writing my function
document, and noticed that we don't need "math.inc" anymore - at least not in
3.8. :)
> But for your matrix illustrations, I don't know if they should be used (since I
> don't know enough about matrix math).
I just put sin and cos because everyone everywhere knows what that is and I
would hope that most people would assume that it's implied that there's a
degrees - to - radians conversion... But "matrix math" is no different than
"spreadsheet math" or pencil and paper math or chalkboard math.... it's just a
way of laying things out so that the values in the places are operated on by the
appropriate values in the places of other matrices. Or that the formulas for
things like determinants are using the right values. No magic.
It's just an organizational thing to make the notation compact.
Just think about it as: array {Vec.x, Vec.y, Vec.z} and then make a 2D array
with 2 or 3 more vectors....
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()