 |
 |
|
 |
|
 |
|  |
|  |
|
 |
From: kurtz le pirate
Subject: Re: profile following a parametric curve
Date: 1 May 2025 09:53:55
Message: <68137cf3@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 01/05/2025 14:39, Bald Eagle wrote:
> kurtz le pirate <kur### [at] free fr> wrote:
>
>> Curves are defined with Cartesian parameters: x=f(t), z=g(t).
>> The profile is a simple polygon.
>
> Nice job with the profiles.
>
> What's the arc-length of that lemniscate? :D
Simple. Here, half-width a = 24 = c√2.
2*π
Then, length = --------- * c
M(1,1/√2)
With M(a,b) the arithmetic–geometric mean function.
;)
--
kurtz le pirate
compagnie de la banquise fr> wrote:
>
>> Curves are defined with Cartesian parameters: x=f(t), z=g(t).
>> The profile is a simple polygon.
>
> Nice job with the profiles.
>
> What's the arc-length of that lemniscate? :D
Simple. Here, half-width a = 24 = c√2.
2*π
Then, length = --------- * c
M(1,1/√2)
With M(a,b) the arithmetic–geometric mean function.
;)
--
kurtz le pirate
compagnie de la banquise
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 5/1/25 06:22, kurtz le pirate wrote:
> My first attempts.
>
> Curves are defined with Cartesian parameters: x=f(t), z=g(t).
> The profile is a simple polygon.
Cool!
Bill P.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] free fr> wrote:
> Simple. Here, half-width a = 24 = c√2.
>
> 2*π
> Then, length = --------- * c
> M(1,1/√2)
>
>
Maybe not so simple?
https://en.wikipedia.org/wiki/Elliptic_function#History
(I only know that because I was trying to hunt down a good overview of
calculating the arc-length of a catenary, and move along the curve at regular
intervals.)
- BW fr> wrote:
> Simple. Here, half-width a = 24 = c√2.
>
> 2*π
> Then, length = --------- * c
> M(1,1/√2)
>
>
Maybe not so simple?
https://en.wikipedia.org/wiki/Elliptic_function#History
(I only know that because I was trying to hunt down a good overview of
calculating the arc-length of a catenary, and move along the curve at regular
intervals.)
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 01/05/2025 17:37, Bald Eagle wrote:
> kurtz le pirate <kur### [at] free fr> wrote:
>
>> Simple. Here, half-width a = 24 = c√2.
>>
>> 2*π
>> Then, length = --------- * c
>> M(1,1/√2)
>>
>>
>> With M(a,b) the arithmetic–geometric mean function.
>
> Maybe not so simple?
> https://en.wikipedia.org/wiki/Elliptic_function#History
That's right.
But my answer is more of a joke and a simple copy/paste from Wiki
<https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli#Arc_length_and_elliptic_functions>
--
kurtz le pirate
compagnie de la banquise fr> wrote:
>
>> Simple. Here, half-width a = 24 = c√2.
>>
>> 2*π
>> Then, length = --------- * c
>> M(1,1/√2)
>>
>>
>> With M(a,b) the arithmetic–geometric mean function.
>
> Maybe not so simple?
> https://en.wikipedia.org/wiki/Elliptic_function#History
That's right.
But my answer is more of a joke and a simple copy/paste from Wiki
<https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli#Arc_length_and_elliptic_functions>
--
kurtz le pirate
compagnie de la banquise
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] free fr> wrote:
> That's right.
>
> But my answer is more of a joke and a simple copy/paste from Wiki
>
<https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli#Arc_length_and_elliptic_functions>
Nice. (I suspected)
"It therefore obviously follows that . . ." ;)
- BW fr> wrote:
> That's right.
>
> But my answer is more of a joke and a simple copy/paste from Wiki
>
<https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli#Arc_length_and_elliptic_functions>
Nice. (I suspected)
"It therefore obviously follows that . . ." ;)
- BW
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] free fr> wrote:
> hello,
>
>
> My first attempts.
>
> Curves are defined with Cartesian parameters: x=f(t), z=g(t).
> The profile is a simple polygon.
>
> Basic texture, lighting with area_light.
> Low resolution (800x600).
>
>
>
>
>
>
>
>
> --
> kurtz le pirate
> compagnie de la banquise
Do you adjust the size of your profile object as you follow the curve, or does
it just have a very tiny thickness at each t step? When I use this technique, I
struggle with getting the resulting object smooth if the curves are wide.
-- Chris R fr> wrote:
> hello,
>
>
> My first attempts.
>
> Curves are defined with Cartesian parameters: x=f(t), z=g(t).
> The profile is a simple polygon.
>
> Basic texture, lighting with area_light.
> Low resolution (800x600).
>
>
>
>
>
>
>
>
> --
> kurtz le pirate
> compagnie de la banquise
Do you adjust the size of your profile object as you follow the curve, or does
it just have a very tiny thickness at each t step? When I use this technique, I
struggle with getting the resulting object smooth if the curves are wide.
-- Chris R
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 02/05/2025 16:17, Chris R wrote:
>
> Do you adjust the size of your profile object as you follow the curve, or does
> it just have a very tiny thickness at each t step? When I use this technique, I
> struggle with getting the resulting object smooth if the curves are wide.
>
> -- Chris R
>
Hello Chris.
In fact, my profile has no thickness !
The profile is only defined by points in an a array and doesn't really
exist.
For example, the profile for a triangle is defined like this:
#declare i = 0;
#while ( i < NumberOfVertices)
#declare ShapePoints[i] = RotateX(<0, ShapeRadius, 0>, Angle*i);
#declare i = i +1;
#end
The shape is in the y-z plane.
I position the first profile for t=0;
Then I calculate the position for the second (t=t+epsilon) and build
triangles* that connect the two profiles.
* : using the true POV object : triangle { p0, p1, p2 }
--
kurtz le pirate
compagnie de la banquise
Post a reply to this message
Attachments:
Download 'parametrique_limacon de pascal _connect_prof0.png' (124 KB)
Preview of image 'parametrique_limacon de pascal _connect_prof0.png'
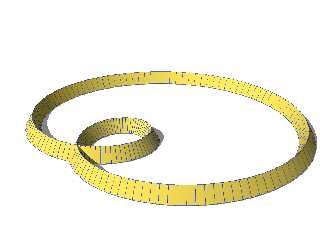
|
 |
|  |
|  |
|
 |
From: kurtz le pirate
Subject: Re: profile following a parametric curve
Date: 3 May 2025 11:18:56
Message: <681633e0@news.povray.org>
|
|
 |
|  |
|  |
|
 |
A little more artistic, but this time using a curve defined by a polar
equation.
Profile : hexagon.
Low resolution (800x600).
--
kurtz le pirate
compagnie de la banquise
Post a reply to this message
Attachments:
Download 'polaire_trefle_connect_0.png' (264 KB)
Preview of image 'polaire_trefle_connect_0.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] free fr> wrote:
> On 02/05/2025 16:17, Chris R wrote:
> >
> > Do you adjust the size of your profile object as you follow the curve, or does
> > it just have a very tiny thickness at each t step? When I use this technique, I
> > struggle with getting the resulting object smooth if the curves are wide.
> >
> > -- Chris R
> >
>
>
> Hello Chris.
>
> In fact, my profile has no thickness !
> The profile is only defined by points in an a array and doesn't really
> exist.
>
>
> For example, the profile for a triangle is defined like this:
> #declare i = 0;
> #while ( i < NumberOfVertices)
> #declare ShapePoints[i] = RotateX(<0, ShapeRadius, 0>, Angle*i);
> #declare i = i +1;
> #end
> The shape is in the y-z plane.
>
> I position the first profile for t=0;
>
> Then I calculate the position for the second (t=t+epsilon) and build
> triangles* that connect the two profiles.
>
> * : using the true POV object : triangle { p0, p1, p2 }
>
>
>
>
> --
> kurtz le pirate
> compagnie de la banquise
Thanks for the explanation. My brain is so focused on isosurfaces and
extrusions that I didn't even think of using triangles or a mesh.
-- Chris R fr> wrote:
> On 02/05/2025 16:17, Chris R wrote:
> >
> > Do you adjust the size of your profile object as you follow the curve, or does
> > it just have a very tiny thickness at each t step? When I use this technique, I
> > struggle with getting the resulting object smooth if the curves are wide.
> >
> > -- Chris R
> >
>
>
> Hello Chris.
>
> In fact, my profile has no thickness !
> The profile is only defined by points in an a array and doesn't really
> exist.
>
>
> For example, the profile for a triangle is defined like this:
> #declare i = 0;
> #while ( i < NumberOfVertices)
> #declare ShapePoints[i] = RotateX(<0, ShapeRadius, 0>, Angle*i);
> #declare i = i +1;
> #end
> The shape is in the y-z plane.
>
> I position the first profile for t=0;
>
> Then I calculate the position for the second (t=t+epsilon) and build
> triangles* that connect the two profiles.
>
> * : using the true POV object : triangle { p0, p1, p2 }
>
>
>
>
> --
> kurtz le pirate
> compagnie de la banquise
Thanks for the explanation. My brain is so focused on isosurfaces and
extrusions that I didn't even think of using triangles or a mesh.
-- Chris R
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 05/05/2025 15:32, Chris R wrote:
>
> Thanks for the explanation. My brain is so focused on isosurfaces and
> extrusions that I didn't even think of using triangles or a mesh.
more explanations on my website ;)
--
kurtz le pirate
compagnie de la banquise
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()