|
 |
On 03/12/2023 03:36, Bald Eagle wrote:
> For any triangle, one can find 3 circles that are all tangent to 2 sides of the
> triangle and the 2 other circles.
>
> Crazy stuff. :)
>
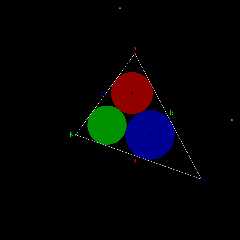
Malfatti circles !!!
Complicated but very interesting problem ...
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
|
 |
|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
> Malfatti circles !!!
> Complicated but very interesting problem ...
Yeah - while working on the Japanese kumiko triangles, I ran across some
related/linked work from an artist:
https://www.flickr.com/photos/quasimondo/
Then I just recently, and randomly, stumbled across Stephane Laurent's work, who
has apparently been doing some amazing work in POV-Ray, R, Python, JS3, and
Asymptote.
https://www.youtube.com/@stla3716/videos
https://www.r-bloggers.com/
With the way links and references get lost, and search results evaporate, I
needed to grab it while it was there and port it to POV-Ray before it
disappeared.
Porting from R was only minorly confusing in a few places, and of course, I had
a typo in my code, which was driving me nuts, and the circle centers (the part
that has been holding me back from coding it myself) are located with ....
trilinear coordinates! I started having flashbacks.
It would be nice to figure out how to translate it all into functions so that it
could be applied to the triangular pigment patterns....
- BW com> wrote:
> Malfatti circles !!!
> Complicated but very interesting problem ...
Yeah - while working on the Japanese kumiko triangles, I ran across some
related/linked work from an artist:
https://www.flickr.com/photos/quasimondo/
Then I just recently, and randomly, stumbled across Stephane Laurent's work, who
has apparently been doing some amazing work in POV-Ray, R, Python, JS3, and
Asymptote.
https://www.youtube.com/@stla3716/videos
https://www.r-bloggers.com/
With the way links and references get lost, and search results evaporate, I
needed to grab it while it was there and port it to POV-Ray before it
disappeared.
Porting from R was only minorly confusing in a few places, and of course, I had
a typo in my code, which was driving me nuts, and the circle centers (the part
that has been holding me back from coding it myself) are located with ....
trilinear coordinates! I started having flashbacks.
It would be nice to figure out how to translate it all into functions so that it
could be applied to the triangular pigment patterns....
- BW
Post a reply to this message
|
 |
|
 |
On 04/12/2023 20:16, Bald Eagle wrote:
> kurtz le pirate <kur### [at] gmail com> wrote:
>
>> Malfatti circles !!!
>> Complicated but very interesting problem ...
>
> Yeah - while working on the Japanese kumiko triangles, I ran across some
> related/linked work from an artist:
>
> https://www.flickr.com/photos/quasimondo/
>
> Then I just recently, and randomly, stumbled across Stephane Laurent's work, who
> has apparently been doing some amazing work in POV-Ray, R, Python, JS3, and
> Asymptote.
> https://www.youtube.com/@stla3716/videos
> https://www.r-bloggers.com/
>
> With the way links and references get lost, and search results evaporate, I
> needed to grab it while it was there and port it to POV-Ray before it
> disappeared.
> Porting from R was only minorly confusing in a few places, and of course, I had
> a typo in my code, which was driving me nuts, and the circle centers (the part
> that has been holding me back from coding it myself) are located with ....
> trilinear coordinates! I started having flashbacks.
>
> It would be nice to figure out how to translate it all into functions so that it
> could be applied to the triangular pigment patterns....
>
> - BW
>
Hi,
With a few head-scratchers. I used my "basic" method and classic
geometry : normals, parallels, intersections ...
Still some debugging to do to find right parallels : uppper ou lower the
line.
I don't think it's possible to turn them into functions that can be used
as reasons for completing the plan. But who knows ?
ps : yes, trilinear coordinates is a nightmare ;)
--
Kurtz le pirate
Compagnie de la Banquise com> wrote:
>
>> Malfatti circles !!!
>> Complicated but very interesting problem ...
>
> Yeah - while working on the Japanese kumiko triangles, I ran across some
> related/linked work from an artist:
>
> https://www.flickr.com/photos/quasimondo/
>
> Then I just recently, and randomly, stumbled across Stephane Laurent's work, who
> has apparently been doing some amazing work in POV-Ray, R, Python, JS3, and
> Asymptote.
> https://www.youtube.com/@stla3716/videos
> https://www.r-bloggers.com/
>
> With the way links and references get lost, and search results evaporate, I
> needed to grab it while it was there and port it to POV-Ray before it
> disappeared.
> Porting from R was only minorly confusing in a few places, and of course, I had
> a typo in my code, which was driving me nuts, and the circle centers (the part
> that has been holding me back from coding it myself) are located with ....
> trilinear coordinates! I started having flashbacks.
>
> It would be nice to figure out how to translate it all into functions so that it
> could be applied to the triangular pigment patterns....
>
> - BW
>
Hi,
With a few head-scratchers. I used my "basic" method and classic
geometry : normals, parallels, intersections ...
Still some debugging to do to find right parallels : uppper ou lower the
line.
I don't think it's possible to turn them into functions that can be used
as reasons for completing the plan. But who knows ?
ps : yes, trilinear coordinates is a nightmare ;)
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
Attachments:
Download 'malfatti2.png' (34 KB)
Preview of image 'malfatti2.png'
|
 |




![]()