 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I was playing around with the examples on Mike William's Isosurface Tutorial
page (excellent site, I bookmarked it and refer to it constantly). The one
I'm focused on is a parametric lathe that uses a spline to define different
profiles in two axes. I'm wondering if there is a way to produce a similar
object without the point at the top. I tried moving the endpoint of the
spline closer to the second point but the object distorts as if there is an
asymptote there. What I'm looking for is an object bound by splines with
rounded ends. Here is an example rendering and the code used to generate
it:
// Almost a lathe
#version 3.5;
camera { location <3, 3, -5> look_at <0, 0, 0> angle 25}
sky_sphere { pigment {
function{abs(y)}
color_map { [0.0 color blue 0.6] [1.0 color rgb 1] }
}
}
light_source {<100,200,-500> colour rgb 1}
// The open 1D spline (lathe)
#declare S = function {
spline {
natural_spline
-1, < 0.0, 0, 0.0>,
-0.8, < 0.4, 0, 0.5>,
-0.5, < 0.2, 0, 0.2>,
-0.2, < 0.2, 0, 0.2>,
0.3, < 0.8, 0, 0.4>,
0.4, < 0.0, 0, 0.0>
}
}
#declare Fx = function(x,y) {(S(u).x * sin(v)/2)}
#declare Fy = function(x,y) {u}
#declare Fz = function(x,y) {(S(u).z * cos(v)/2)}
#declare Umin = -1;
#declare Umax = 1;
#declare Vmin = -pi;
#declare Vmax = 1.001*pi;
parametric {
function {Fx(u,v)}
function {Fy(u,v)}
function {Fz(u,v)}
<Umin,Vmin>,<Umax,Vmax>
contained_by{box{-1,1}}
precompute 18, x,y,z
pigment {rgb 0.9}
finish {phong 0.5 phong_size 10 ambient 0.2}
}
Post a reply to this message
Attachments:
Download 'param.jpg' (7 KB)
Preview of image 'param.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Skip Talbot" <sta### [at] uiuc edu> schrieb im Newsbeitrag
news:40581849$1@news.povray.org...
> I was playing around with the examples on Mike William's Isosurface
Tutorial
> page (excellent site, I bookmarked it and refer to it constantly). The
one
> I'm focused on is a parametric lathe that uses a spline to define
different
> profiles in two axes. I'm wondering if there is a way to produce a
similar
> object without the point at the top. I tried moving the endpoint of the
> spline closer to the second point but the object distorts as if there is
an
> asymptote there. What I'm looking for is an object bound by splines with
> rounded ends. Here is an example rendering and the code used to generate
> it:
Hi Skip,
to get a smooth tip you ideally would have an infinite gradient where your
splinefunction reaches the tip (has value 0.0). But since the spline is
still a function it can only have a finite gradient, so with your technique
you will always have a more or less spiky tip. But in practice it's in most
cases sufficient to have a moderately high gradient at the tip.
You have to experiment a bit with your spline, especially because if you
take
the gradient to the extreme you will distort the shape of your object too
much.
> // The open 1D spline (lathe)
> #declare S = function {
> spline {
> natural_spline
> -1, < 0.0, 0, 0.0>,
> -0.8, < 0.4, 0, 0.5>,
> -0.5, < 0.2, 0, 0.2>,
> -0.2, < 0.2, 0, 0.2>,
> 0.3, < 0.8, 0, 0.4>,
> 0.4, < 0.0, 0, 0.0>
> }
> }
I fiddled a bit with the spline..
This looks reasonably well for me :
#declare S = function {
spline {
natural_spline
-1.1, <-1.00, 0,-1.25>,
-1.0, < 0.00, 0, 0.00>,
-0.8, < 0.40, 0, 0.50>,
-0.5, < 0.20, 0, 0.20>,
-0.2, < 0.20, 0, 0.20>,
0.3, < 0.80, 0, 0.40>,
0.4, < 0.00, 0, 0.00>
0.5, <-2.00, 0,-1.00>
}
}
Here you can see that extremer values distort the shape also :
#declare S = function {
spline {
natural_spline
-1.1, <-2.00, 0,-2.50>,
-1.0, < 0.00, 0, 0.00>,
-0.8, < 0.40, 0, 0.50>,
-0.5, < 0.20, 0, 0.20>,
-0.2, < 0.20, 0, 0.20>,
0.3, < 0.80, 0, 0.40>,
0.4, < 0.00, 0, 0.00>
0.5, <-4.00, 0,-2.00>
}
}
To cut the shape at the apex you should also use
#declare Umax = 0.4;
instead of
#declare Umax = 1;
Hope this was helpful,
Thies edu> schrieb im Newsbeitrag
news:40581849$1@news.povray.org...
> I was playing around with the examples on Mike William's Isosurface
Tutorial
> page (excellent site, I bookmarked it and refer to it constantly). The
one
> I'm focused on is a parametric lathe that uses a spline to define
different
> profiles in two axes. I'm wondering if there is a way to produce a
similar
> object without the point at the top. I tried moving the endpoint of the
> spline closer to the second point but the object distorts as if there is
an
> asymptote there. What I'm looking for is an object bound by splines with
> rounded ends. Here is an example rendering and the code used to generate
> it:
Hi Skip,
to get a smooth tip you ideally would have an infinite gradient where your
splinefunction reaches the tip (has value 0.0). But since the spline is
still a function it can only have a finite gradient, so with your technique
you will always have a more or less spiky tip. But in practice it's in most
cases sufficient to have a moderately high gradient at the tip.
You have to experiment a bit with your spline, especially because if you
take
the gradient to the extreme you will distort the shape of your object too
much.
> // The open 1D spline (lathe)
> #declare S = function {
> spline {
> natural_spline
> -1, < 0.0, 0, 0.0>,
> -0.8, < 0.4, 0, 0.5>,
> -0.5, < 0.2, 0, 0.2>,
> -0.2, < 0.2, 0, 0.2>,
> 0.3, < 0.8, 0, 0.4>,
> 0.4, < 0.0, 0, 0.0>
> }
> }
I fiddled a bit with the spline..
This looks reasonably well for me :
#declare S = function {
spline {
natural_spline
-1.1, <-1.00, 0,-1.25>,
-1.0, < 0.00, 0, 0.00>,
-0.8, < 0.40, 0, 0.50>,
-0.5, < 0.20, 0, 0.20>,
-0.2, < 0.20, 0, 0.20>,
0.3, < 0.80, 0, 0.40>,
0.4, < 0.00, 0, 0.00>
0.5, <-2.00, 0,-1.00>
}
}
Here you can see that extremer values distort the shape also :
#declare S = function {
spline {
natural_spline
-1.1, <-2.00, 0,-2.50>,
-1.0, < 0.00, 0, 0.00>,
-0.8, < 0.40, 0, 0.50>,
-0.5, < 0.20, 0, 0.20>,
-0.2, < 0.20, 0, 0.20>,
0.3, < 0.80, 0, 0.40>,
0.4, < 0.00, 0, 0.00>
0.5, <-4.00, 0,-2.00>
}
}
To cut the shape at the apex you should also use
#declare Umax = 0.4;
instead of
#declare Umax = 1;
Hope this was helpful,
Thies
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
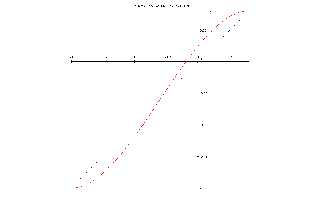
I just had another idea:
If you take a new function for your y-coordinate (which
varies linearly with u at the moment) you can have a smooth
tip. Imagine that you wander along your y-axis as u increases
from -1 to 0.4 eventually. If you start slowly, get more pace
in the middle and slow down near the end you get a smooth tip.
(I made a graph to show the y-function dependent on u).
The cubic u^2*(3-2*u) is ideal for this purpose because it
has zero-slope at u=0 and u=1. The only problem is that our
u varies from [-1, 0.4] instead of [0, 1], so we have to make
a small transformation to get our u in the range [0, 1]. We
just substitute u with (u+1)/1.4 and get the u-range right.
The last step is the scaling in y-direction, because
u^2*(3-2*u) returns values in the range [0, 1]. In summary:
u^2*(3-2*u) // set (u+1)/1.4 for u
-> ((u+1)/1.4)^2*(3-(u+1)/1.4) // *1.4 // -1
-> 1.4*((u+1)/1.4)^2*(3-(u+1)/1.4)-1
The Source looks like this:
// Almost a lathe
#version 3.5;
camera { location <3, 3, -5> look_at <0, 0, 0> angle 25}
sky_sphere { pigment {
function{abs(y)}
color_map { [0.0 color blue 0.6] [1.0 color rgb 1] }
}
}
light_source {<100,200,-500> colour rgb 1}
// The open 1D spline (lathe)
#declare S = function {
spline {
natural_spline
-1.0, < 0.0, 0, 0.0>,
-0.8, < 0.4, 0, 0.5>,
-0.5, < 0.2, 0, 0.2>,
-0.2, < 0.2, 0, 0.2>,
0.3, < 0.8, 0, 0.4>,
0.4, < 0.0, 0, 0.0>,
}
}
#declare Fx = function(x,y) {(S(u).x * sin(v)/2)}
#declare Fy = function(x,y)
{1.4*(5/7*(u+1))*(5/7*(u+1))*(3-2*(5/7*(u+1)))-1}
#declare Fz = function(x,y) {(S(u).z * cos(v)/2)}
#declare Umin = -1;
#declare Umax = 0.4;
#declare Vmin = -pi;
#declare Vmax = 1.001*pi;
parametric {
function {Fx(u,v)}
function {Fy(u,v)}
function {Fz(u,v)}
<Umin,Vmin>,<Umax,Vmax>
contained_by{box{-1,1}}
precompute 18, x,y,z
pigment {rgb 0.9}
finish {phong 0.5 phong_size 10 ambient 0.2}
}
Post a reply to this message
Attachments:
Download 'u-coordinate.png' (8 KB)
Download 'almost_lathe.JPG' (7 KB)
Preview of image 'u-coordinate.png'
Preview of image 'almost_lathe.JPG'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Sorry to be so blunt Skip, but that doesn't look anything like a Deset
Eagle. :-)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
That's why I need the pointy tips to be gone.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Ah ha! Now I get it, lose the points, put a mirror behind it and ta-da!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Fantastic, thanks Thies!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()