On 22/12/2021 06:51, Tor Olav Kristensen wrote:
> Hi
>
> Since this post:
>
> From: kurtz le pirate
> Subject: How to ...
> Date: 2021-11-22 11:23:08
> http://news.povray.org/povray.general/thread/%3C619bc3ec%241%40news.povray.org%3E/
>
> - I've been working on some some macros that create functions for calculating
> with complex numbers.
>
> And yesterday I made some functions that can be used for HSV-coloring of
> pigments.
>
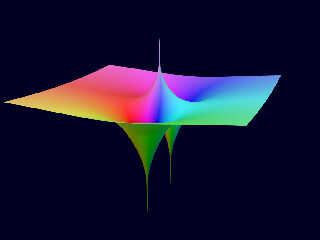
> The isosurface in the attached image shows the magnitude (or modulus) of this
> function:
>
> Fn(Z) = 1/(Z^5 - 2)^2
>
> - as the height above a complex plane:. I found that function here:
>
https://matlabarticlesworld.blogspot.com/2020/01/what-is-coolest-thing-you-can-do-with.html
>
> The colors are chosen so that the hue follows the phase (or argument) of the
> function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> axis. The saturation is 100% everywhere.
Very good job !
The basic operators on the complexes is much more elaborate than mine. I
use simple macros. This makes the definitions a little more difficult to
work out. For example, for f(z) = z + 1/z, I have to write
complexAdd(cc,complexInverse(cc)).
The really interesting part is the use of isosurfaces. Good job. I just
used colored triangles which give me a {} mesh. The coloring model is
also very clever because the hue and luminosity depend on the value of
the function.
I will see how to add the same coloring scheme as you.
Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
Attachments:
Download 'complex3dmesh_02_fn2.jpg' (48 KB)
Preview of image 'complex3dmesh_02_fn2.jpg'
|




![]()