|
 |
On 10/7/19 1:07 PM, jr wrote:
> hi,
>
> William F Pokorny <ano### [at] anonymous org> wrote:
>> Perhaps, finally, a good test case for isosurface artefacts I've worked
>> around for years! Confirmation Windows / OSX showing similar artefacts
>> would be useful. Linux users not on Ubuntu 18.04 too.
>> ...
>
> same artefacts (identical looking) on a Slackware box, using
> 3.8.0-alpha.10013324.unofficial.
>
> regards, jr.
>
Thanks jr.
Well... What's going on is subtle and it's an exposure in all continuous
patterns used with pigments, isosurfaces, whatever.
The root is the SDL use of mod() or, internal to POV-Ray itself, the use
of fmod() when executing this bit of code - used by all but the two
potential patterns currently(2):
if(waveFrequency != 0.0)
value = fmod(value * waveFrequency + wavePhase, 1.00001); \
// TODO FIXME - magic number! ....
or this bit when functions are used in pattern{} / virtual pattern blocks:
DBL value = GenericScalarFunctionInstance(pFn, \
pThread).Evaluate(EPoint);
return ((value > 1.0) ? fmod(value, 1.0) : value);
When the mod()/fmod() numerator value is a harmonic of the denominator,
the resultant value suddenly jumps to 0.0 - though that's not always the
right thing to do.
In the example scene image I was normalizing the discontinuities of
tiling 11 so it acts like a linear displacement function for the
isosurface sheet. The denominator is therefore 1/3 and harmonics of that
go to 0. Further, due my container sides being at -1,+1 I'm sitting on a
harmonic and I get spurious shapes.
However, it's a general pattern problem. Should users specify a pattern
frequency value >1 or use a similar multiplier for a function's values,
the multiples of 1, 1.00001 or both, depending, are exposed to harmonics
where the resultant value jumps to zero.
Most often it will be seen with isosurface box containers given they can
somewhat easily have sides exactly on the mod() harmonics. When the
artefact otherwise shows up, it will usually be a line of noise perhaps
the wrong color from a pigment map or similar somewhere is the image.
I've seen and seen reports of such artefacts over the years. Expect this
issue sometimes the cause.
Aside: Yes, the pattern { function { } } treatment is different than
what pattern { } or pigment { agate/etc .... } does, which is not good.
The former does a better job of of deciding when to apply fmod and does
it correctly with a denominator of 1.0 - but it ignores the negative
value space. The latter has that odd 1.00001 denominator(2); the odd
skipping of calculations when the frequency is 0.0 - and negative values
are inverted by magnitude. The last something OK with defined patterns
(gradient x etc), but potentially confusing and sometimes at odds with
functions(1). Weird stuff can happen with a function's negative values
due pattern use.
I've used the trick of specifying a frequency 0 when going after a
little more performance, but I've come up with no reason to not let a
user take the resultant values to 0 using frequency 0. In fact, that
with phase provides a nice way of walking a *_map.
Unsure what all to do here, but certainly going to fix what I can in my
POV-Ray version.
---
Generally we want - on the mod(numerator/denominator) harmonics to
return the actual value divided by div(numerator/denominator) - instead
of 0.0. On a 5 day driving trip from LA to NYC across America, it makes
no sense to fly back to sleep in LA every night. :-)
We need updates for the two bits of code above in pattern.cpp and we
need a new inbuilt VM function which implements the smarter mod()/fmod()
to zero - only when we really want zero - functionality. Currently
calling it f_npmod() - normalized pattern mod(). Also passing an extra
multiplier to allow normalization back to a 0-1 range.
I have a first pass f_npmod() and pattern.cpp updates. Tested creating
isosurface 'sheets' from all 27 tiling patterns. 15 of those originally
hit the mod()/fmod() jump to zero issue. My initial code cleaned up all
but 6 of those. 4 of those 6 had other numerical issues in the tiling
code like not clamping to 1.0 where the old 1.00001 fmod allowed the
tiny overrun.
I'm left with two tiling patterns still an issue in tilings 19 and 20.
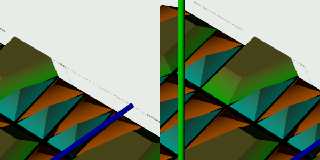
I'm attaching an image for 20 showing the initial pattern.cpp 'mod'
fixes and new f_mpmod function. These partly fixed issues in 19 and 20
as seen left to right - but there is still something wrong. It looks
like an incorrect count in x or similar at the isosurface z sides is
part of it, but I've not found the problem(s).
----
Aside: All through the tiling code there are bits and comments like:
answer = max(answer, 2.000001); // TODO FIXME - magic number! Should
use nextafter()
In the tilings changed, I checked nextafter() and never did it work as
an alternative. Thus far, the magic numbers look to be addressing real
numerical issues. I've changed these lines to read:
answer = max(answer, 2.0+1e-7); // +1e-7 add & magnitude due
numerical fuzziness.
or similar.
It's been the case the original extra amounts has ranged between 1e-6
and 1e-8, but in all cases 1e-7 worked fine. Interestingly, the value
adjustments are of a similar order of magnitude to the min intersection
depth I settled on with the solver accuracy work (4.4e-8).
---
Expect I'll play for quite a while with my changes before opening a
github issue and publishing a code branch. All patterns are touched by
my changes. In the meantime, you have my ramblings - for what they're worth.
Bill P.
(1) - Perhaps allow too fabs() with pattern { functions {} } over
if(value<0) value -= floor(value);. I don't know. Whatever might come
would be an option so as to not break scenes built on the current
inverting of the negative (0-1) magnitudes. I've done nothing with this
secondary concern around using other than >=0 valued functions as patterns.
(2) - The odd 1.00001 fmod denominator has largely hidden the base issue
- forever. Why someone did it I'd bet. Not very often will usage land
exactly on a harmonic of 1.00001. org> wrote:
>> Perhaps, finally, a good test case for isosurface artefacts I've worked
>> around for years! Confirmation Windows / OSX showing similar artefacts
>> would be useful. Linux users not on Ubuntu 18.04 too.
>> ...
>
> same artefacts (identical looking) on a Slackware box, using
> 3.8.0-alpha.10013324.unofficial.
>
> regards, jr.
>
Thanks jr.
Well... What's going on is subtle and it's an exposure in all continuous
patterns used with pigments, isosurfaces, whatever.
The root is the SDL use of mod() or, internal to POV-Ray itself, the use
of fmod() when executing this bit of code - used by all but the two
potential patterns currently(2):
if(waveFrequency != 0.0)
value = fmod(value * waveFrequency + wavePhase, 1.00001); \
// TODO FIXME - magic number! ....
or this bit when functions are used in pattern{} / virtual pattern blocks:
DBL value = GenericScalarFunctionInstance(pFn, \
pThread).Evaluate(EPoint);
return ((value > 1.0) ? fmod(value, 1.0) : value);
When the mod()/fmod() numerator value is a harmonic of the denominator,
the resultant value suddenly jumps to 0.0 - though that's not always the
right thing to do.
In the example scene image I was normalizing the discontinuities of
tiling 11 so it acts like a linear displacement function for the
isosurface sheet. The denominator is therefore 1/3 and harmonics of that
go to 0. Further, due my container sides being at -1,+1 I'm sitting on a
harmonic and I get spurious shapes.
However, it's a general pattern problem. Should users specify a pattern
frequency value >1 or use a similar multiplier for a function's values,
the multiples of 1, 1.00001 or both, depending, are exposed to harmonics
where the resultant value jumps to zero.
Most often it will be seen with isosurface box containers given they can
somewhat easily have sides exactly on the mod() harmonics. When the
artefact otherwise shows up, it will usually be a line of noise perhaps
the wrong color from a pigment map or similar somewhere is the image.
I've seen and seen reports of such artefacts over the years. Expect this
issue sometimes the cause.
Aside: Yes, the pattern { function { } } treatment is different than
what pattern { } or pigment { agate/etc .... } does, which is not good.
The former does a better job of of deciding when to apply fmod and does
it correctly with a denominator of 1.0 - but it ignores the negative
value space. The latter has that odd 1.00001 denominator(2); the odd
skipping of calculations when the frequency is 0.0 - and negative values
are inverted by magnitude. The last something OK with defined patterns
(gradient x etc), but potentially confusing and sometimes at odds with
functions(1). Weird stuff can happen with a function's negative values
due pattern use.
I've used the trick of specifying a frequency 0 when going after a
little more performance, but I've come up with no reason to not let a
user take the resultant values to 0 using frequency 0. In fact, that
with phase provides a nice way of walking a *_map.
Unsure what all to do here, but certainly going to fix what I can in my
POV-Ray version.
---
Generally we want - on the mod(numerator/denominator) harmonics to
return the actual value divided by div(numerator/denominator) - instead
of 0.0. On a 5 day driving trip from LA to NYC across America, it makes
no sense to fly back to sleep in LA every night. :-)
We need updates for the two bits of code above in pattern.cpp and we
need a new inbuilt VM function which implements the smarter mod()/fmod()
to zero - only when we really want zero - functionality. Currently
calling it f_npmod() - normalized pattern mod(). Also passing an extra
multiplier to allow normalization back to a 0-1 range.
I have a first pass f_npmod() and pattern.cpp updates. Tested creating
isosurface 'sheets' from all 27 tiling patterns. 15 of those originally
hit the mod()/fmod() jump to zero issue. My initial code cleaned up all
but 6 of those. 4 of those 6 had other numerical issues in the tiling
code like not clamping to 1.0 where the old 1.00001 fmod allowed the
tiny overrun.
I'm left with two tiling patterns still an issue in tilings 19 and 20.
I'm attaching an image for 20 showing the initial pattern.cpp 'mod'
fixes and new f_mpmod function. These partly fixed issues in 19 and 20
as seen left to right - but there is still something wrong. It looks
like an incorrect count in x or similar at the isosurface z sides is
part of it, but I've not found the problem(s).
----
Aside: All through the tiling code there are bits and comments like:
answer = max(answer, 2.000001); // TODO FIXME - magic number! Should
use nextafter()
In the tilings changed, I checked nextafter() and never did it work as
an alternative. Thus far, the magic numbers look to be addressing real
numerical issues. I've changed these lines to read:
answer = max(answer, 2.0+1e-7); // +1e-7 add & magnitude due
numerical fuzziness.
or similar.
It's been the case the original extra amounts has ranged between 1e-6
and 1e-8, but in all cases 1e-7 worked fine. Interestingly, the value
adjustments are of a similar order of magnitude to the min intersection
depth I settled on with the solver accuracy work (4.4e-8).
---
Expect I'll play for quite a while with my changes before opening a
github issue and publishing a code branch. All patterns are touched by
my changes. In the meantime, you have my ramblings - for what they're worth.
Bill P.
(1) - Perhaps allow too fabs() with pattern { functions {} } over
if(value<0) value -= floor(value);. I don't know. Whatever might come
would be an option so as to not break scenes built on the current
inverting of the negative (0-1) magnitudes. I've done nothing with this
secondary concern around using other than >=0 valued functions as patterns.
(2) - The odd 1.00001 fmod denominator has largely hidden the base issue
- forever. Why someone did it I'd bet. Not very often will usage land
exactly on a harmonic of 1.00001.
Post a reply to this message
Attachments:
Download 'tiling20_story.png' (64 KB)
Preview of image 'tiling20_story.png'
|
 |




![]()