Adding the inbuilt functions: f_bezier_2d_linear() 
f_bezier_2d_quadratic() f_bezier_2d_cubic() f_bezier_2d_quartic() and 
f_bezier_2d_quintic() to the next yuqk release (R19).

The functions take and return single float packed 2d vectors in a 
double's space for control points and return values. Calculations are at 
double float accuracy internal to each functions code. The t parameter 
is passed as a double.

The calculation and return mode settings:
   0=<u,v> at t.
   1=<u',v'> at t.             (Tangent normalized)
   2=<normal u,normal v> at t. ((1) rotated for normal)
   3=<u',v'> at t.             (Tangent / velocity)
   4=<u'',v''> at t.           (Acceleration / change in tangent)
   5=<u''',v'''> at t.         (Jerk / change in acceleration)

Attaching images showing all six calculation and return modes for 
f_bezier_2d_cubic() f_bezier_2d_quartic() and f_bezier_2d_quintic().

Bill P.


Extra Detail
------------

The code approach settled upon will I believe easily map to 3D vectors 
excepting the normal mode (2) calculations. Holding off though, I'd like 
to play with this new 2d code for a while and, as inbuilt functions, 
we'd end up working in a three, 21bit, float packed, reduced range for 
the easy 3D adoption.

---

IIRC, Bald Eagle asked whether the derivatives weren't lower orders of 
the Bezier curve itself. I currently believe the answer to be, yes, with 
qualifications.

First, there are compensating factors for each derivative order based 
upon the initial Bezier curve:

Quadratic derivative factors:
   '   --> 2
   ''  --> 2
   ''' --> DNA

Cubic derivative factors:
   '   --> 3
   ''  --> 6
   ''' --> 6

Quartic derivative factors:
   '   --> 4
   ''  --> 12
   ''' --> 24

Quintic derivative factors:
   '   --> 5
   ''  --> 20
   ''' --> 60

I used 1/(factors above) multipliers to better view the raw 1st, 2nd and 
3rd derivative value curves(*) (modes 4,5 and 6) together. The 
derivative value curves(*) tend to get much larger as the derivative 
order increases.

Second, some algebra is required to come up with the new P' factors for 
each derivative Bezier curve.

(*) - The curves are showing the entire sample set of values as spheres. 
The strict sphere(t) curve may have folds where parts of the apparent 
curve are getting retraced.

---

Post a reply to this message

Attachments:
Download 'f_bezier_2d_cubicstory.png' (18 KB) Download 'f_bezier_2d_quarticstory.png' (31 KB) Download 'f_bezier_2d_quinticstory.png' (30 KB)

Preview of image 'f_bezier_2d_cubicstory.png'

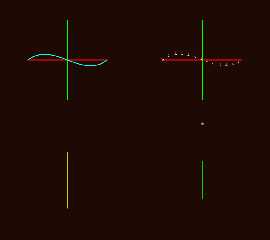
Preview of image 'f_bezier_2d_quarticstory.png'

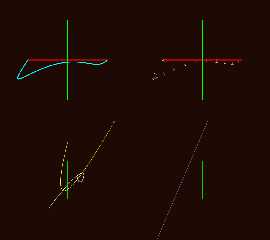
Preview of image 'f_bezier_2d_quinticstory.png'
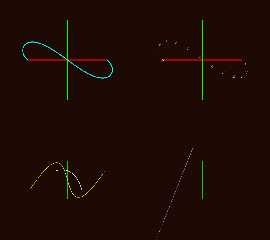