Invisible wrote:

> That's quite nice, but a cursory inspection of the JavaScript code 
> reveals how it works: In effect, the first keypress starts a timer. The 
> displayed BPM is simply the time elapsed between the first and most 
> recent keypress divided by the total number of presses.
> 
> Now I'm wondering if I can come up with something a little more 
> accurate. (Although, obviously, accuracy is ultimately determined by how 
> good your coordination and sense of rhythm are!)

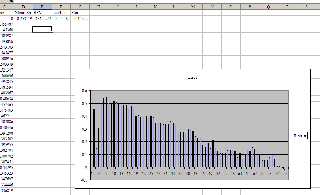
Take a look at the attachments.

The first one shows the normal prediction method - take the duration of 
time between the first and last tap, divide by the number of taps. This 
gives you the beat period (i.e., seconds/beat). The BPM figure is just 
the reciprocol of this (with some conversion of units).

As you can see, if you compare the predicted beat times to the actual 
taps entered, there's quite a lot of error. But, more seriously, the 
error shows a pronounced linear trend. In other words, the BPM figure is 
wrong, causing the taps and the prediction to gradually change their 
phase relationship.

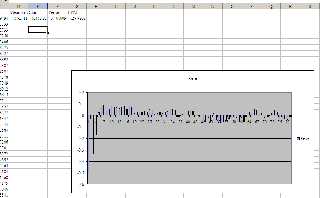
Now take a look at the second attachment. This is produced using a 
propper linear regression. (Simple least squares, apparently.) Here the 
algorithm has quite rightly detected that the first few taps are 
horribly out of time, while the remaining ones fit neatly onto a regular 
beat grid at 129.98 BPM (verses the 131.72 BPM detected by the other 
method).

I notice there's still a slight linear trend to the errors, so maybe the 
true BPM figure is actually lower still.

What the first method is doing is basically setting the prediction error 
of the first and last tap to exactly zero, and linearly interpolating 
between. This works horribly if the first and/or last taps are 
particularly out of time. It's basically using 2 data points to detect 
the right BPM figure.

On the other hand, I'm not sure, but I'd guess that *least squares* 
linear regression probably assigns a large penalty to points with large 
errors. In other words, out-of-time points are especially significant. 
Obviously what *I* want is for out-of-time points to be especially 
*insignificant*. I want to maximise the number of points with low 
errors, not minimise the total error size.

Also, I have no idea how to compute a confidence value for the 
regression predictions, other than by using the statistics of the tap 
time-deltas as an estimate...

Post a reply to this message

Attachments:
Download 'bpm1.png' (25 KB) Download 'bpm2.png' (21 KB)

Preview of image 'bpm1.png'

Preview of image 'bpm2.png'

Invisible wrote:
> Now take a look at the second attachment. This is produced using a 
> propper linear regression. (Simple least squares, apparently.)

In solomn truth, both the simple and fancy algorithms tend to produce 
very similar results, given the same data. Regression fit produces 
smaller error values by getting the phase alignment correct, but they 
both report roughly the same BPM reading.

Also, they are both equally perplexed by missing / additional beat 
signals, so I need to go figure that out...

Post a reply to this message

> Also, they are both equally perplexed by missing / additional beat 
> signals, so I need to go figure that out...

With your array of times-between-beats, calculate the mean and sd of the 
whole array, then remove any entries that are outside of the mean +/- N*sd 
before you do your BPM calculation.  You can choose N based on the results, 
but I guess around 1 should work.

Post a reply to this message

scott wrote:
>> Also, they are both equally perplexed by missing / additional beat 
>> signals, so I need to go figure that out...
> 
> With your array of times-between-beats, calculate the mean and sd of the 
> whole array, then remove any entries that are outside of the mean +/- 
> N*sd before you do your BPM calculation.  You can choose N based on the 
> results, but I guess around 1 should work.

Yes, that's more or less my plan. I just haven't coded it yet.

Post a reply to this message

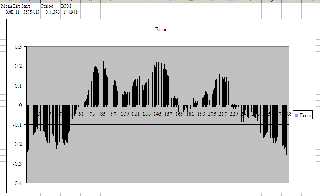
I had expected the taps to be approximately correct, but jittered either 
side of the correct points by a roughly normal distribution. However, 
this is not what I observe.

Take a look at the first attachment. There's an obvious U-shapred trend 
in the error graph, and I have no idea why. It appears very, very 
frequently though. But aside from that, the errors look much more like a 
random walk than a normal distrubition. The timing error in each tap 
appears to be highly correlated with its neighbors.

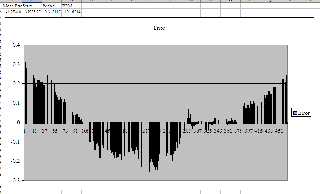
The second attachment shows a similar pattern (although the U-shapred 
trend is now inverted). Note the difference in tempo between the two 
examples.

I hypothesize that what actually happens is that my tapping is actually 
running off an internal mental clock, which is being adjusted by a 
feedback loop that keeps it reasonably in-phase with the actual 
drumbeat. Hence the random-walk variations.

Of course, it's possible that the music I'm tapping to actually contains 
subtle tempo variations. Or that some of these patterns are prediction 
errors. I think what I need to do is perform a tapping experiment with a 
timing source of known tempo, so I can get genuine error measurements. 
(Currently it's tricky to reperate human tapping errors from computer 
prediction errors.)

Post a reply to this message

Attachments:
Download 'bpm1.png' (14 KB) Download 'bpm2.png' (16 KB)

Preview of image 'bpm1.png'

Preview of image 'bpm2.png'

Invisible wrote:

> I think what I need to do is perform a tapping experiment with a 
> timing source of known tempo, so I can get genuine error measurements. 

Heh, this is more difficult than you'd imagine.

I wrote a small program that basically does

   Get wall time.
   Save wall time to file.
   Print something to stdout.
   Wait X seconds.
   Repeat.

The amount of time is computed from the requested BPM. Only trouble is, 
when I analysed the resulting data, I discovered that the program is 
ticking too slowly. (E.g., I request 135 BPM, but I get 128 BPM.)

So then I tried having a thread that just does

   Send signal.
   Wait X seconds.
   Repeat.

and another thread that waits to receive a signal, and then does all the 
other stuff. But noooo, the timing accuracy has increased, but it's 
still ticking too slowly.

Thing is, what I want to do isn't "wait until X seconds from now", it's 
"wait until time X". But there isn't a function to do that. If there 
was, I could take the wall time now, compute the correct time for all 
future clock ticks, and schedule the thread to run at those times. But 
there isn't.

So I started digging through the library source code. Oh, this is fun: 
Internally the "wait X seconds" function is implemented using a "wait 
until time X" function. But it's private, so I can't call it. Thanks, 
guys...

Next plan: Write out a WAV file containing sonic pulses with the correct 
timing. Because, let's face it, there isn't much that can go wrong here.

Post a reply to this message

On 6/9/2010 5:18 AM, Invisible wrote:


> I hypothesize that what actually happens is that my tapping is actually
> running off an internal mental clock, which is being adjusted by a
> feedback loop that keeps it reasonably in-phase with the actual
> drumbeat. Hence the random-walk variations.

Am I the only one who thought PLL when I read this?


-- 
~Mike

Post a reply to this message

>> I hypothesize that what actually happens is that my tapping is actually
>> running off an internal mental clock, which is being adjusted by a
>> feedback loop that keeps it reasonably in-phase with the actual
>> drumbeat. Hence the random-walk variations.
> 
> Am I the only one who thought PLL when I read this?

No, that's pretty much what I was thinking when I wrote it...

Post a reply to this message

> and another thread that waits to receive a signal, and then does all the 
> other stuff. But noooo, the timing accuracy has increased, but it's still 
> ticking too slowly.

If you can call API functions, call QueryPerformanceCounter from 
Kernel32.dll.  It is pretty much the ultimate in terms of useful timing 
accuracy and resolution under windows.  It only takes one parameter (a 
pointer to a 64-bit signed integer) so should be easy to set up if you don't 
have the header.

Post a reply to this message

>>> I hypothesize that what actually happens is that my tapping is actually
>>> running off an internal mental clock, which is being adjusted by a
>>> feedback loop that keeps it reasonably in-phase with the actual
>>> drumbeat. Hence the random-walk variations.
>>
>> Am I the only one who thought PLL when I read this?
>
> No, that's pretty much what I was thinking when I wrote it...

I also thought about it when I suggested to write code to find the BPM 
automatically.

Post a reply to this message