Invisible wrote:

> That's quite nice, but a cursory inspection of the JavaScript code 
> reveals how it works: In effect, the first keypress starts a timer. The 
> displayed BPM is simply the time elapsed between the first and most 
> recent keypress divided by the total number of presses.
> 
> Now I'm wondering if I can come up with something a little more 
> accurate. (Although, obviously, accuracy is ultimately determined by how 
> good your coordination and sense of rhythm are!)

Take a look at the attachments.

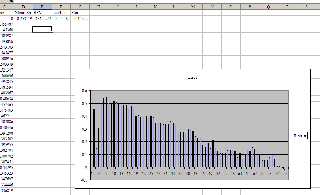
The first one shows the normal prediction method - take the duration of 
time between the first and last tap, divide by the number of taps. This 
gives you the beat period (i.e., seconds/beat). The BPM figure is just 
the reciprocol of this (with some conversion of units).

As you can see, if you compare the predicted beat times to the actual 
taps entered, there's quite a lot of error. But, more seriously, the 
error shows a pronounced linear trend. In other words, the BPM figure is 
wrong, causing the taps and the prediction to gradually change their 
phase relationship.

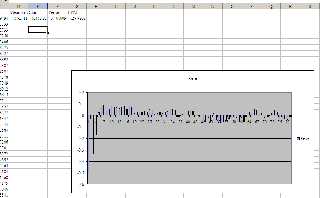
Now take a look at the second attachment. This is produced using a 
propper linear regression. (Simple least squares, apparently.) Here the 
algorithm has quite rightly detected that the first few taps are 
horribly out of time, while the remaining ones fit neatly onto a regular 
beat grid at 129.98 BPM (verses the 131.72 BPM detected by the other 
method).

I notice there's still a slight linear trend to the errors, so maybe the 
true BPM figure is actually lower still.

What the first method is doing is basically setting the prediction error 
of the first and last tap to exactly zero, and linearly interpolating 
between. This works horribly if the first and/or last taps are 
particularly out of time. It's basically using 2 data points to detect 
the right BPM figure.

On the other hand, I'm not sure, but I'd guess that *least squares* 
linear regression probably assigns a large penalty to points with large 
errors. In other words, out-of-time points are especially significant. 
Obviously what *I* want is for out-of-time points to be especially 
*insignificant*. I want to maximise the number of points with low 
errors, not minimise the total error size.

Also, I have no idea how to compute a confidence value for the 
regression predictions, other than by using the statistics of the tap 
time-deltas as an estimate...

Post a reply to this message

Attachments:
Download 'bpm1.png' (25 KB) Download 'bpm2.png' (21 KB)

Preview of image 'bpm1.png'

Preview of image 'bpm2.png'