On 5/5/20 1:34 PM, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymousorg> wrote:
> 
...
> With regard to dot notations and vectors - what is the "native form" for a
> pigment pattern?  Is it an "rgb" vector where each component simply has the same
> value unless modified by a color_map?
> 
> And is it therefore slower to use .gray or .hf?
> 

You got it. Yes, it's slower to use .gray or .hf if, say, .red will do. 
However, often not by enough you can really tell given the volatility of 
today's CPU performance.

We also have the issue POV-Ray's .gray, .grey and .hf functions not 
being quite the norm. Somewhere there are posts from Christoph - and 
maybe Cousin Ricky - on this IIRC. I have notes somewhere...

I've been staying away from .gray, .grey and .hf and output to grey file 
formats for a while.

I think so long as all rgb values match exactly the difference in 
POV-Ray's conversion to a gray value doesn't matter - but that statement 
should be thoroughly tested before being set in stone.

Bill P.

Post a reply to this message

On 5/5/20 1:34 PM, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymousorg> wrote:
> 
>> I'm going make another attempt at an inbuilt function for this. If
>> you've tweaked something in the code from the previous few posts, please
>> let me know.
> 
> Nope - Just been playing around with it a bit to make sure the outer and inner
> shapes are truly elliptical (they are).
> 
...
> 

A quick note and image.

I ran at an f_elliptical_torus() again today and again failed. Ended up 
almost exactly where I did last time for result. :-(

My implementation of your recent code worked straight up with different 
a=b sizes this time. When a=b we match Bruno's result - and that of 
f_torus() for that matter. When A close to B results is pretty close as 
in the top row, but if A and B much different it falls apart.

FYI. I'm comparing against Bruno's sphere_sweep version which looks good 
to me for shape and OK for comparisons. However, the sphere_sweep itself 
won't render at all cleanly in some orientations / sizes due bugs with 
the sphere_sweep if using v37 / v38. My povr updates mostly work with 
the orthographic camera - except for some speckles you can see in the 
comparisons.

Aside: The orthographic rays to a flat sphere_sweep the worst case 
solver wise because the two roots collapse to a multiple with which 
solvers struggle. I have a patch in TCL for some of these (missed roots 
after polynomial deflation), but not yet found myself putting it in.

If the mood hits me, I'll spend some time trying to digest what Bruno 
really did. Review too my version of your code, but this time not too 
different from yours. Might try your SDL straight up - I didn't do that 
this time... Work for another day.

Bill P.

Post a reply to this message

Attachments:
Download 'eltorusfail.jpg' (91 KB)

Preview of image 'eltorusfail.jpg'

On 2020-05-04 3:56 AM (-4), William F Pokorny wrote:
> 
> FYI. I've not recently looked at it, but back in 2006 Bruno Cabasson 
> worked up some code for elliptical tori implemented with sphere_sweeps 
> and blobs. Perhaps useful to review that work as we look for an 
> f_elliptical_torus() or complete parametric solution.
> 
> Given we can use blobs as potential patterns in functions/isosurfaces in 
> v38, perhaps this a path to something practical for Cousin Ricky?
> 
> The sphere_sweep as a general solution is not very attractive in v37 and 
> prior due bugs. Situations is better in v38 - and still better in povr 
> but the sphere_sweep probably not the fastest.
> 
> With both approaches expect tolerances to any math ideal, but perhaps we 
> are stuck with a fuzzy result in any case?

Sphere sweeps are unsatisfactory.  The attachment shows that the inner 
and outer curves are not ellipses.  The discrepancy does decrease with 
the ratio of the minor radius to the major radii and the eccentricity of 
the shape, but I would prefer a mathematical match at all scales.

Post a reply to this message

Attachments:
Download 'why_not_sswp.jpg' (61 KB)

Preview of image 'why_not_sswp.jpg'

On 2020-05-02 9:27 AM (-4), Bald Eagle wrote:
> Hopefully this is to spec.
> 
> The green circles are torus{} objects to show that the cross section is indeed
> exactly circular.
> 
> Not my best work, and it's only a parametric, not an implicit equation, but
> perhaps  I can "implicitize" it.

Converting it to an isosurface with a table gradient will be the hard 
part.  I don't know what to do with parametrics; I might have put in the 
work if they didn't take longer to render than refraction and dispersion 
with media and radiosity.

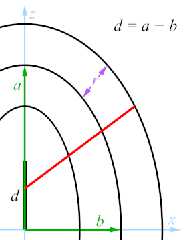
These are some diagrams that I worked out in 2008.  They led me to a 
quartic equation, which I predicted (but haven't verified) would become 
8th order when converted to 3-D.  I never did solve the equation.  My 
last attempt that I remember was in 2010, and those worksheets are 
currently in storage (along with most of my possessions) while home 
repairs progress(?).

Note that the minor radius does not project to the origin except at the 
elliptical vertices and co-vertices.

Even without direct conversion to 3-D, the solution could be adapted for 
isosurface ellipses with roughly isodirectional gradients, which could 
easily be converted to toroids with RE_fn_Blob2()--although blobbing a 
shape that has already been treated with RE_fn_Blob2() would be rather slow.

Also attached is a test of an equation posted by Nicolas George at the 
time.  It looks remarkably similar to Bill's May 8th fail.  Nicolas 
appears to have taken exactly the approach that I had rejected, namely 
to project the minor radius back to the origin.  In fairness to him, I 
had not posted my diagrams.  His post is at
   https://news.povray.org/48fe0ebe%241%40news.povray.org
in response to my thread.

Post a reply to this message

Attachments:
Download 'elliptor-eq.png' (52 KB) Download 'elliptor-fig.png' (18 KB) Download 'elliptical_torus-iso.jpg' (72 KB)

Preview of image 'elliptor-eq.png'

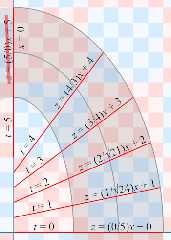
Preview of image 'elliptor-fig.png'

Preview of image 'elliptical_torus-iso.jpg'

On 2020-05-02 9:27 AM (-4), Bald Eagle wrote:
> Hopefully this is to spec.
> 
> The green circles are torus{} objects to show that the cross section is indeed
> exactly circular.
> 
> Not my best work, and it's only a parametric, not an implicit equation, but
> perhaps  I can "implicitize" it.

This is a test of an equation posted by Sebastian H in 2006.  The shape 
appears to be exact, but the max_gradient is a nightmare, and I don't 
know how it stable the gradients are.  The post is at:
   https://news.povray.org/4409cd2a%40news.povray.org

Post a reply to this message

Attachments:
Download 'sebastian-elliptor-test4.jpg' (59 KB) Download 'sebastian-elliptor-test70-4.jpg' (48 KB)

Preview of image 'sebastian-elliptor-test4.jpg'

Preview of image 'sebastian-elliptor-test70-4.jpg'

On 5/8/20 9:29 PM, Cousin Ricky wrote:
> On 2020-05-02 9:27 AM (-4), Bald Eagle wrote:
....
> 

> appears to be exact, but the max_gradient is a nightmare, and I don't 

> > https://news.povray.org/4409cd2a%40news.povray.org

Ah... Thanks. I would probably not have jumped in knowing all that 
ahead. I was only aware of Bruno's work and his only because I was 
looking for sphere_sweep and blob test cases for my solver work.

I've captured all the information in my f_torus working directory.

My gut when I first read your list of requirements was that there was 
probably no exact solution. That the requirements force some 
discontinuity / fuzz. Is this thinking proven wrong somewhere?

I was on a path that solutions like Bruno's were OK / useful enough... 
If I run at this again I'll probably try and implement the blob like 
solution on the fly as a solution for something I can use.

Sebastian's images mention compares to a mesh. Of what mesh was he 
speaking? Something created from an exact solution? Something in your 
package somewhere?

Did you see my recent post to povray.general on the parametric 
performance being better than we've thought all these years? Default 
gradient of 1.0 should be more like 0.001.

Supposing there is an exact solution for the elliptical tori you want. 
Any 8th order equation will be somewhat sloppy with respect to solutions 
(165 terms were mentioned in the one post. If not sparse...).

My personal interests lean toward something with good gradients in a 
range which will play well with all the other stuff I'm doing. Solutions 
a little sloppy, but fast, and good enough are OK with me. :-)

Bill P.

Post a reply to this message

On 2020-05-09 8:48 AM (-4), William F Pokorny wrote:
> On 5/8/20 9:29 PM, Cousin Ricky wrote:

>> shape appears to be exact, but the max_gradient is a nightmare, and I 

>> > https://news.povray.org/4409cd2a%40news.povray.org
> 
> Ah... Thanks. I would probably not have jumped in knowing all that 
> ahead. I was only aware of Bruno's work and his only because I was 
> looking for sphere_sweep and blob test cases for my solver work.
> 
> I've captured all the information in my f_torus working directory.
> 
> My gut when I first read your list of requirements was that there was 
> probably no exact solution. That the requirements force some 
> discontinuity / fuzz. Is this thinking proven wrong somewhere?

Based on my work in 2008, I'm pretty sure there is an exact solution. 
The key seemed to be in solving a quartic equation, although the 
equation itself would not be the whole solution.

> Sebastian's images mention compares to a mesh. Of what mesh was he 
> speaking? Something created from an exact solution? Something in your 
> package somewhere?

I created the mesh using RoundEdge::RE_Elliptorus_mesh(), then 
co-located it with Sebastian's isosurface.  The mesh2 is built up in a 
parametric fashion using sines and cosines.

> Did you see my recent post to povray.general on the parametric 
> performance being better than we've thought all these years? Default 
> gradient of 1.0 should be more like 0.001.

No, I haven't see it yet.

> Supposing there is an exact solution for the elliptical tori you want. 
> Any 8th order equation will be somewhat sloppy with respect to solutions 
> (165 terms were mentioned in the one post. If not sparse...).

I'm aware of that.  I even wrote a JavaScript that shows me the POV-Ray 
order of coefficients for the poly object, although it has since been 
rendered redundant by 3.7's new polynomial syntax.

Every poly I've had occasion to use has been sparse.  While I don't have 
an intuitive feel for these things, I don't see why an elliptical toroid 
would break this pattern.

> My personal interests lean toward something with good gradients in a 
> range which will play well with all the other stuff I'm doing. Solutions 
> a little sloppy, but fast, and good enough are OK with me. :-)

I guess I could take "good enough" if it can sneak by our eyes' 
simultaneous contrast.  But simultaneous contrast is surprisingly 
sensitive.  The attached renders of the lever cap cam of a hand plane 
use deformations of an isosurface oblong toroid that was "good enough," 
but it is easy to see the mismatch between the toroid and the scaled 
cylinder.  This was a few months before my initial upload of RoundEdge; 
I was hopeful of finding a solution, but decided to post the module 
without the toroid rather than include a poor solution.

Post a reply to this message

Attachments:
Download 'cam-blob.jpg' (13 KB) Download 'cam-oblique.jpg' (17 KB)

Preview of image 'cam-blob.jpg'

Preview of image 'cam-oblique.jpg'

On 5/9/20 12:07 PM, Cousin Ricky wrote:
> On 2020-05-09 8:48 AM (-4), William F Pokorny wrote:
...

Ah, blast. Thank you for posting those 'lever cap cam' images.

Wondering in this moment if the 'failed' attempts were me having the 
wrong visual expectation for what you need. Pretty sure what you need 
has to pinch between the orthogonal axes for that lever thing. I've been 
working against that result.

Let me see if I can get a test set up going with a parametric as the 
reference.

Bill P.

Post a reply to this message

OK folks,

This is certainly challenging, but bit by bit, I think we're drawing closer to
figuring out where the difficulty is, and what is needed to overcome it.

I would be very interested in seeing the quartic equation, or at least the best
recollection of how it was derived.

As [creepily] often happens, I've had this tab open in my browser for quite some
time, but with the shader autoplay blocked by Brave, I didn't fully grasp what
it was about.

https://www.iquilezles.org/www/articles/distance/distance.htm

This was very exciting to me, as it solves some problems I've had with sine
waves and offset curves.
But as you can see, it also fixes the scaling of the thickness of an ellipse.
You can imagine this being used to fix a torus scaled into an elliptical torus.

https://www.shadertoy.com/view/MdfGWn
https://www.shadertoy.com/view/4tSfRz

I worked on it for a while, and got the simple 2D ellipse to work nicely, but
the 3D extrapolation to the torus didn't quite work out.

But then I thought - if one method is "off" one way, and this method is "off"
the other, .... then what happens if I blend them - will they cancel each other
out?

Almost.

What I've noticed while playing with parameters is that as Ricky observed, the
errors are accentuated by eccentricity and minor radius size.  Those errors seem
to be a shrinking effect in my original isosurface, and an expansion in the new
equation.  That error seems to be due to too much "z" at the ends, which then
tapers off as the curve approaches the z axis.

I haven't gotten the numerical gradient correction to work properly (yet), but
the approach makes sense, it feels like the right way to go due to its
simplicity, and most of my experiments had a max_gradient around 26.

The attached render has a gradient of 1770, but I rendered it with a holdover
value of only 355.

Post a reply to this message

Attachments:
Download 'implicitellipticaltorus_modgrad.png' (186 KB)

Preview of image 'implicitellipticaltorus_modgrad.png'

"Bald Eagle" <cre### [at] netscapenet> wrote:

> This was very exciting to me, as it solves some problems I've had with sine
> waves and offset curves.
> But as you can see, it also fixes the scaling of the thickness of an ellipse.
> You can imagine this being used to fix a torus scaled into an elliptical torus.

AND .... this same approach was implemented by ... user And in 2013 to make
constant-thickness isosurface shells.

http://news.povray.org/povray.binaries.images/thread/%3Cweb.5264d1b954cff585cc1fd1150%40news.povray.org%3E/?ttop=423056
&toff=750&mtop=423452&moff=10

Post a reply to this message