 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
So, I've been trying half a dozen ways to make a shape, and I managed to work
out the equations to do it with an isosurface.
(because OMG are parametrics SLOOOOOOW)
Only the frequency of the sine wave for the serrated, lemon-juicer top doesn't
look right, and it's hard to really see what's going wrong with all of the
unexpected noise.
#declare ISphereR = 24;
#declare I_Phi = function {tan(z/x)}
#declare F_Sphere = function {pow(x,2)+pow(y,2)+pow(z,2) - pow(ISphereR,2)}
// a sine wave 80% of full size, with 3 peaks
#declare F_Wave = function {ISphereR*0.8 * sin(3*I_Phi(x, y, z))}
// only generate a spherical isosurface for the parts where the height
// is less than the sine wave function
#declare I = function {select(F_Wave(x,y,z)-y, 0, 0, 1)}
//----------------For debugging---------------------------
//#declare S_Wave = function {I(x,y,z)*F_Sphere(x,y,z)}
//--------------------------------------------------------
#declare S_Wave = function {select(y, F_Sphere (x, y, z),
I(x,y,z)*F_Sphere(x,y,z))}
#declare Gradient = 5500;
#declare Min_factor= 0.7;
#declare I_Surface = isosurface {
//function {Pattern(x, y, z).red - 0.5}
function {S_Wave (x, y, z)}
open
threshold 0
max_gradient 5500
//evaluate Gradient*Min_factor, sqrt(Gradient/(Gradient*Min_factor)), min
(0.7, 1.0)
accuracy 0.1
contained_by {box {<-1, -1, -1>*ISphereR*1.1, <1, 1, 1>*ISphereR*1.1}}
}
Post a reply to this message
Attachments:
Download 'isosurface.png' (88 KB)
Preview of image 'isosurface.png'

|
 |
|  |
|  |
|
 |
From: Subclick
Subject: Re: Crummy isosurface evaluation.
Date: 17 Feb 2020 21:54:53
Message: <s6uzhdgehad.fsf@sp.am>
|
|
 |
|  |
|  |
|
 |
If I understand its purpose correctly, the I_Phi function should be
#declare I_Phi = function {atan2(z, x)}
F_Wave should probably converge to a constant (the amplitude of the wave
vanishing) as (x, 0, z) approaches the origin, rather than continue to
oscillate with a fixed amplitude along an ever tinier circumference,
which produces an unbounded gradient. For example,
#declare F_Wave = function
{0.8*sqrt(pow(x,2)+pow(z,2))*sin(3*I_Phi(x, 0, z))}
You’ll probably want more than three ridges, however.
Note your I function has an infinite gradient on the y = F_Wave(x, y, z)
surface. You could instead do something like
#declare F_Cap = function
{pow(x,2)+pow(max(y,0),2)+pow(z,2) - pow(ISphereR,2)}
#declare S_Wave = function {F_Cap(x, y - F_Wave(x, y, z), z)}
The 0.8 factor in F_Wave may need tweaking.
Now you need to cut off with an intersection or differencethe part of
the isosurface below the y = 0 plane, adjust the “contained_by” object
and put the result in a union or merge with half a sphere object, which
I think will be faster to render than retaining the lower hemisphere as
part of the isosurface.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Subclick <no### [at] sp am> wrote:
> If I understand its purpose correctly, the I_Phi function should be
> #declare I_Phi = function {atan2(z, x)}
Yeah - I often try to do this stuff while juggling 3 other things, 2
conversations, and a 10 yo playing/commenting on video games right next to me.
I had the same feeling but not enough conviction at the time to make the change.
> F_Wave should probably converge to a constant (the amplitude of the wave
> vanishing) as (x, 0, z) approaches the origin, rather than continue to
> oscillate with a fixed amplitude along an ever tinier circumference,
> which produces an unbounded gradient.
Yep, that's likely the insight I was missing.
> For example,
> #declare F_Wave = function
> {0.8*sqrt(pow(x,2)+pow(z,2))*sin(3*I_Phi(x, 0, z))}
> You’ll probably want more than three ridges, however.
>
> Note your I function has an infinite gradient on the y = F_Wave(x, y, z)
> surface. You could instead do something like
> #declare F_Cap = function
> {pow(x,2)+pow(max(y,0),2)+pow(z,2) - pow(ISphereR,2)}
> #declare S_Wave = function {F_Cap(x, y - F_Wave(x, y, z), z)}
> The 0.8 factor in F_Wave may need tweaking.
>
> Now you need to cut off with an intersection or differencethe part of
> the isosurface below the y = 0 plane, adjust the “contained_by” object
> and put the result in a union or merge with half a sphere object, which
> I think will be faster to render than retaining the lower hemisphere as
> part of the isosurface.
Lots to digest and experiment and learn from, as always.
As complex as the present form may seem, it's still just an overly simplified
model. What I'm shooting for is attached, and I really don't want to do it as
CSG, because the elegant form just SCREAMS "minimal surface" or "algebraic
surface". It has curves and round transitions, and circular arcs and parabolas
that all just _flow_.
Thank you for your excellent help and suggestions - it will certainly help
reorient my thoughts in pursuing this challenging project. am> wrote:
> If I understand its purpose correctly, the I_Phi function should be
> #declare I_Phi = function {atan2(z, x)}
Yeah - I often try to do this stuff while juggling 3 other things, 2
conversations, and a 10 yo playing/commenting on video games right next to me.
I had the same feeling but not enough conviction at the time to make the change.
> F_Wave should probably converge to a constant (the amplitude of the wave
> vanishing) as (x, 0, z) approaches the origin, rather than continue to
> oscillate with a fixed amplitude along an ever tinier circumference,
> which produces an unbounded gradient.
Yep, that's likely the insight I was missing.
> For example,
> #declare F_Wave = function
> {0.8*sqrt(pow(x,2)+pow(z,2))*sin(3*I_Phi(x, 0, z))}
> You’ll probably want more than three ridges, however.
>
> Note your I function has an infinite gradient on the y = F_Wave(x, y, z)
> surface. You could instead do something like
> #declare F_Cap = function
> {pow(x,2)+pow(max(y,0),2)+pow(z,2) - pow(ISphereR,2)}
> #declare S_Wave = function {F_Cap(x, y - F_Wave(x, y, z), z)}
> The 0.8 factor in F_Wave may need tweaking.
>
> Now you need to cut off with an intersection or differencethe part of
> the isosurface below the y = 0 plane, adjust the “contained_by” object
> and put the result in a union or merge with half a sphere object, which
> I think will be faster to render than retaining the lower hemisphere as
> part of the isosurface.
Lots to digest and experiment and learn from, as always.
As complex as the present form may seem, it's still just an overly simplified
model. What I'm shooting for is attached, and I really don't want to do it as
CSG, because the elegant form just SCREAMS "minimal surface" or "algebraic
surface". It has curves and round transitions, and circular arcs and parabolas
that all just _flow_.
Thank you for your excellent help and suggestions - it will certainly help
reorient my thoughts in pursuing this challenging project.
Post a reply to this message
Attachments:
Download 'disk.png' (241 KB)
Preview of image 'disk.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
>
> So, I've been trying half a dozen ways to make a shape, and I managed to work
> out the equations to do it with an isosurface.
> (because OMG are parametrics SLOOOOOOW)
>
>
> Only the frequency of the sine wave for the serrated, lemon-juicer top doesn't
> look right, and it's hard to really see what's going wrong with all of the
> unexpected noise.
>
> #declare ISphereR = 24;
> #declare I_Phi = function {tan(z/x)}
> #declare F_Sphere = function {pow(x,2)+pow(y,2)+pow(z,2) - pow(ISphereR,2)}
you are working with a scale of 1 unit = 1mm, that's still a radius of
57.6 cm, or a diameter of 1.15m.
>
> // a sine wave 80% of full size, with 3 peaks
> #declare F_Wave = function {ISphereR*0.8 * sin(3*I_Phi(x, y, z))}
> // only generate a spherical isosurface for the parts where the height
> // is less than the sine wave function
> #declare I = function {select(F_Wave(x,y,z)-y, 0, 0, 1)}
>
> //----------------For debugging---------------------------
> //#declare S_Wave = function {I(x,y,z)*F_Sphere(x,y,z)}
> //--------------------------------------------------------
> #declare S_Wave = function {select(y, F_Sphere (x, y, z),
> I(x,y,z)*F_Sphere(x,y,z))}
>
>
> #declare Gradient = 5500;
> #declare Min_factor= 0.7;
> #declare I_Surface = isosurface {
> //function {Pattern(x, y, z).red - 0.5}
> function {S_Wave (x, y, z)}
> open
> threshold 0
> max_gradient 5500
> //evaluate Gradient*Min_factor, sqrt(Gradient/(Gradient*Min_factor)), min
> (0.7, 1.0)
> accuracy 0.1
> contained_by {box {<-1, -1, -1>*ISphereR*1.1, <1, 1, 1>*ISphereR*1.1}}
> }
>
Do you realize that
sqrt(Gradient/(Gradient*Min_factor)) = sqrt(1/Min_factorf) ?
For the base sphere, you can use the internal one.
#include "function.inc"
then, use f_sphere(x,y,z, Radius)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Alain Martel <kua### [at] videotron ca> wrote:
.... because the equation of a sphere is x^2 + y^2 +z^2 = r^2 ?
So I just rearranged it to be x^2 + y^2 +z^2 - r^2 = 0 for the isosurface.
> Do you realize that
> sqrt(Gradient/(Gradient*Min_factor)) = sqrt(1/Min_factorf) ?
Sure - It's just a thing copied from the docs. And it only gets evaluated once
AFAIK, so I just keep it the same for recognition purposes. But good eye.
> For the base sphere, you can use the internal one.
> #include "function.inc"
> then, use f_sphere(x,y,z, Radius)
I can. But I like to see all the moving parts, and a function definition is
less overhead than a whole include file. I wasn't sure what I'd be modifying
as I tweaked all the little bits in my quest.
Thanks as always for keeping a keen eye on the details. :) ca> wrote:
.... because the equation of a sphere is x^2 + y^2 +z^2 = r^2 ?
So I just rearranged it to be x^2 + y^2 +z^2 - r^2 = 0 for the isosurface.
> Do you realize that
> sqrt(Gradient/(Gradient*Min_factor)) = sqrt(1/Min_factorf) ?
Sure - It's just a thing copied from the docs. And it only gets evaluated once
AFAIK, so I just keep it the same for recognition purposes. But good eye.
> For the base sphere, you can use the internal one.
> #include "function.inc"
> then, use f_sphere(x,y,z, Radius)
I can. But I like to see all the moving parts, and a function definition is
less overhead than a whole include file. I wasn't sure what I'd be modifying
as I tweaked all the little bits in my quest.
Thanks as always for keeping a keen eye on the details. :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
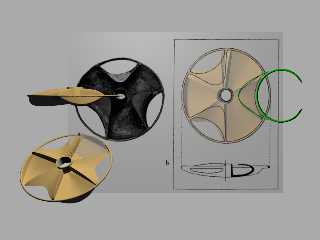
So, just an update to this little project:
I fiddled with some of the functions, and thought more about how best to model
this interesting object.
On the one hand, I'd like to still refine the isosurface approach, ideally
hitting upon a really elegant minimal-surface type approach.
On the other hand, I'd like to get a good representation in a reasonable amount
of time - and it looks like Bezier patches might be the best way to achieve the
smooth, flowing curves.
In the meantime, here's the latest bit of progress trying to harmonize the
"upper" and "lower" sections of the central sheet.
Post a reply to this message
Attachments:
Download 'schistdisk.png' (111 KB)
Preview of image 'schistdisk.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
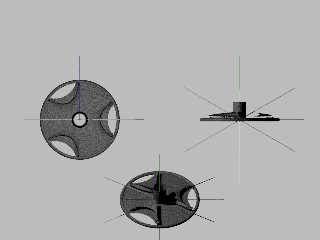
Oh. Yeah.
My intuition was correct, and this looked very much like an Enneper surface of
order 3.
So after much dabbling with the parametric equations, I got rid of some
"twisting", split up the function, add the "curl" to the "wings", and managed to
work out a way to at least get a good look at it with Paul Nylander's
ParametricPlot3D macro.
Then I tweaked it a bit more, and I'd say that I'm _almost_ there. :)
Post a reply to this message
Attachments:
Download 'enneper.png' (69 KB)
Preview of image 'enneper.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()