 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
>
> I'd guess there isn't much use in translating the non-working normal.cpp
> quilted code so below is an my initial attempt at a fix for surfaces
> perpendicular to the x, y and z axis. This updated code passes most of
> my test cases...Whether this is what we want for a
> best quilted fix - I don't know!
The majority of these look quite good, in my opinion, except for odd-looking -H-
(I think one of its control points is negative.) Its inverted(?) pillow look is
kind of hard to discern, though. It would be interesting to see it with a higher
bump value. org> wrote:
>
> I'd guess there isn't much use in translating the non-working normal.cpp
> quilted code so below is an my initial attempt at a fix for surfaces
> perpendicular to the x, y and z axis. This updated code passes most of
> my test cases...Whether this is what we want for a
> best quilted fix - I don't know!
The majority of these look quite good, in my opinion, except for odd-looking -H-
(I think one of its control points is negative.) Its inverted(?) pillow look is
kind of hard to discern, though. It would be interesting to see it with a higher
bump value.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/17/20 10:49 PM, Kenneth wrote:
> William F Pokorny <ano### [at] anonymous org> wrote:
>>
>> I'd guess there isn't much use in translating the non-working normal.cpp
>> quilted code so below is an my initial attempt at a fix for surfaces
>> perpendicular to the x, y and z axis. This updated code passes most of
>> my test cases...Whether this is what we want for a
>> best quilted fix - I don't know!
>
> The majority of these look quite good, in my opinion, except for odd-looking -H-
> (I think one of its control points is negative.) Its inverted(?) pillow look is
> kind of hard to discern, though. It would be interesting to see it with a higher
> bump value.
>
I've attached an hhh.png image with a bump_size of 1 instead of the
default 0.5. The corners are raised relative to the middle parts. The
apparent offset in each cube is due two lights of different colors and
shading due light position.
---
I keep thrashing around on what to do fix wise with the true quilted
normal pattern...
One of the weird things with the existing implementation is the x,y,z
coordinates in the unit cube are all, always used in a distance from
unit cube center calculation. This meant the quilt_cubic function was
getting an over all range of values from 0 to 0.867.
However, at any given face position in the unit cube the range of values
fed to quilt_cubic was in fact a sub range of the 0 to 0.867 range. At
the unit face it was 0.5 to 0.867 (values delta of 0.367). At face
positions moving inward toward 0.0 the delta range moved and increased
in size (to 0.707 on the floor).
We could go a different way for a fix. One which implements the
previous, unit cube centered, face results by default, but which now
offers an offset keyword. The offset would let users slide a 0.367 delta
value range around as fed to the quilt_cubic function. Sort of a left /
right slider for the posted quilt_cubic curves. (Back to the function's
curves having meaning...)
Attached is a second image quiltedOptionTwo.png. The left set of 9 is
the same A to I set. Here it's what users would see at the unit faces
with the existing implementation (ignoring the noise issue). The offset
is 0.5 for these. In the right set of 9, I've used an offset of -1.0.
Many of the faces invert (inside of the pillow) and the results are more
pillow like.
Is this a better way to go for a fix?
This offset keyword would allow users having existing scenes at face
positions not on the full unit cube to achieve a previous result (in
conjunction with bump magnitude) - at least where it wasn't previously
some corrupt, partly inverted result.
Aside: The thrashing here gets back to an early question of Bald
Eagle's. Why not calculate 0-1 face input values for a Bezier curve
where the user specifies both end points in addition to the control
points. It looks to me like this was closer to the form of the original
internal equation; later simplified.
Today suppose, that form of 'quilted_cubic' would better be an inbuilt
function. Users could do what ever they wanted with it. Maybe I'll play
with that too. Could be done with a spline based function, but a limited
inbuilt should be quite a bit faster.
Bill P. org> wrote:
>>
>> I'd guess there isn't much use in translating the non-working normal.cpp
>> quilted code so below is an my initial attempt at a fix for surfaces
>> perpendicular to the x, y and z axis. This updated code passes most of
>> my test cases...Whether this is what we want for a
>> best quilted fix - I don't know!
>
> The majority of these look quite good, in my opinion, except for odd-looking -H-
> (I think one of its control points is negative.) Its inverted(?) pillow look is
> kind of hard to discern, though. It would be interesting to see it with a higher
> bump value.
>
I've attached an hhh.png image with a bump_size of 1 instead of the
default 0.5. The corners are raised relative to the middle parts. The
apparent offset in each cube is due two lights of different colors and
shading due light position.
---
I keep thrashing around on what to do fix wise with the true quilted
normal pattern...
One of the weird things with the existing implementation is the x,y,z
coordinates in the unit cube are all, always used in a distance from
unit cube center calculation. This meant the quilt_cubic function was
getting an over all range of values from 0 to 0.867.
However, at any given face position in the unit cube the range of values
fed to quilt_cubic was in fact a sub range of the 0 to 0.867 range. At
the unit face it was 0.5 to 0.867 (values delta of 0.367). At face
positions moving inward toward 0.0 the delta range moved and increased
in size (to 0.707 on the floor).
We could go a different way for a fix. One which implements the
previous, unit cube centered, face results by default, but which now
offers an offset keyword. The offset would let users slide a 0.367 delta
value range around as fed to the quilt_cubic function. Sort of a left /
right slider for the posted quilt_cubic curves. (Back to the function's
curves having meaning...)
Attached is a second image quiltedOptionTwo.png. The left set of 9 is
the same A to I set. Here it's what users would see at the unit faces
with the existing implementation (ignoring the noise issue). The offset
is 0.5 for these. In the right set of 9, I've used an offset of -1.0.
Many of the faces invert (inside of the pillow) and the results are more
pillow like.
Is this a better way to go for a fix?
This offset keyword would allow users having existing scenes at face
positions not on the full unit cube to achieve a previous result (in
conjunction with bump magnitude) - at least where it wasn't previously
some corrupt, partly inverted result.
Aside: The thrashing here gets back to an early question of Bald
Eagle's. Why not calculate 0-1 face input values for a Bezier curve
where the user specifies both end points in addition to the control
points. It looks to me like this was closer to the form of the original
internal equation; later simplified.
Today suppose, that form of 'quilted_cubic' would better be an inbuilt
function. Users could do what ever they wanted with it. Maybe I'll play
with that too. Could be done with a spline based function, but a limited
inbuilt should be quite a bit faster.
Bill P.
Post a reply to this message
Attachments:
Download 'hhh.png' (87 KB)
Download 'quiltedoptiontwo.png' (343 KB)
Preview of image 'hhh.png'

Preview of image 'quiltedoptiontwo.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> I keep thrashing around on what to do fix wise with the true quilted
> normal pattern...
>
> One of the weird things with the existing implementation is the x,y,z
> coordinates in the unit cube are all, always used in a distance from
> unit cube center calculation. This meant the quilt_cubic function was
> getting an over all range of values from 0 to 0.867.
Yes. None of the vector components ever exceeded +/-0.5, and so
sqrt( pow(x,2) + pow(y,2) + pow(z,2) ) =
sqrt (0.25 + 0.25 + 0.25) =
sqrt (0.75) =
0.866025404
However, you're omitting the fact that the end result of the calculations was
them multiplied by 1/(sqrt(3/4) = 1.154700538
and 0.866025404 * 1.154700538 = 1.0
> However, at any given face position in the unit cube the range of values
> fed to quilt_cubic was in fact a sub range of the 0 to 0.867 range. At
> the unit face it was 0.5 to 0.867 (values delta of 0.367). At face
> positions moving inward toward 0.0 the delta range moved and increased
> in size (to 0.707 on the floor).
Because at N = 0, one of the vector components was always 0, and so the equation
would then be
sqrt (0.25 + 0.25 + 0) =
sqrt (0.5) =
0.707106781
This is the reason why in my initial coding, I instead used a function
incorporating min(max( QX2(x), max(QY2(y), QZ2(z)) ), 0)
(the equation for an isosurface cube)
The idea of course being that such a method should give a constant 1.0 along the
entire surface of any given face.
> We could go a different way for a fix. One which implements the
> previous, unit cube centered, face results by default, but which now
> offers an offset keyword. The offset would let users slide a 0.367 delta
> value range around as fed to the quilt_cubic function. Sort of a left /
> right slider for the posted quilt_cubic curves. (Back to the function's
> curves having meaning...)
Not sure where that comes from:
(0.367.... 0.160? 0.867-0.707?
0.866025404−0.707106781 = 0.158918623)
> This offset keyword would allow users having existing scenes at face
> positions not on the full unit cube to achieve a previous result (in
> conjunction with bump magnitude) - at least where it wasn't previously
> some corrupt, partly inverted result.
Since I got lost and I don't understand, this would be something different that
simply translating the pigment pattern by some amount would _not_ fix?
> Aside: The thrashing here gets back to an early question of Bald
> Eagle's. Why not calculate 0-1 face input values for a Bezier curve
> where the user specifies both end points in addition to the control
> points. It looks to me like this was closer to the form of the original
> internal equation; later simplified.
I'm still confused about a number of points, the most basic and direct is the
graphing of the internal quilted function results vs the documentation graphs.
> Today suppose, that form of 'quilted_cubic' would better be an inbuilt
> function. Users could do what ever they wanted with it. Maybe I'll play
> with that too. Could be done with a spline based function, but a limited
> inbuilt should be quite a bit faster.
Have not been able to invest the uninterrupted and focused time to see where the
interpretation of the quilted function went wrong, or any of that.
But with regard to using a bicubic spline, that is how I got my function to
exhibit the "inflection point" that the documentation graphs show (It's just a
flat tangent=0 point). Actually having a function that allowed a true
inflection point would be interesting - then a tile could have a groove around
the edge, like some cutting boards do. org> wrote:
> I keep thrashing around on what to do fix wise with the true quilted
> normal pattern...
>
> One of the weird things with the existing implementation is the x,y,z
> coordinates in the unit cube are all, always used in a distance from
> unit cube center calculation. This meant the quilt_cubic function was
> getting an over all range of values from 0 to 0.867.
Yes. None of the vector components ever exceeded +/-0.5, and so
sqrt( pow(x,2) + pow(y,2) + pow(z,2) ) =
sqrt (0.25 + 0.25 + 0.25) =
sqrt (0.75) =
0.866025404
However, you're omitting the fact that the end result of the calculations was
them multiplied by 1/(sqrt(3/4) = 1.154700538
and 0.866025404 * 1.154700538 = 1.0
> However, at any given face position in the unit cube the range of values
> fed to quilt_cubic was in fact a sub range of the 0 to 0.867 range. At
> the unit face it was 0.5 to 0.867 (values delta of 0.367). At face
> positions moving inward toward 0.0 the delta range moved and increased
> in size (to 0.707 on the floor).
Because at N = 0, one of the vector components was always 0, and so the equation
would then be
sqrt (0.25 + 0.25 + 0) =
sqrt (0.5) =
0.707106781
This is the reason why in my initial coding, I instead used a function
incorporating min(max( QX2(x), max(QY2(y), QZ2(z)) ), 0)
(the equation for an isosurface cube)
The idea of course being that such a method should give a constant 1.0 along the
entire surface of any given face.
> We could go a different way for a fix. One which implements the
> previous, unit cube centered, face results by default, but which now
> offers an offset keyword. The offset would let users slide a 0.367 delta
> value range around as fed to the quilt_cubic function. Sort of a left /
> right slider for the posted quilt_cubic curves. (Back to the function's
> curves having meaning...)
Not sure where that comes from:
(0.367.... 0.160? 0.867-0.707?
0.866025404−0.707106781 = 0.158918623)
> This offset keyword would allow users having existing scenes at face
> positions not on the full unit cube to achieve a previous result (in
> conjunction with bump magnitude) - at least where it wasn't previously
> some corrupt, partly inverted result.
Since I got lost and I don't understand, this would be something different that
simply translating the pigment pattern by some amount would _not_ fix?
> Aside: The thrashing here gets back to an early question of Bald
> Eagle's. Why not calculate 0-1 face input values for a Bezier curve
> where the user specifies both end points in addition to the control
> points. It looks to me like this was closer to the form of the original
> internal equation; later simplified.
I'm still confused about a number of points, the most basic and direct is the
graphing of the internal quilted function results vs the documentation graphs.
> Today suppose, that form of 'quilted_cubic' would better be an inbuilt
> function. Users could do what ever they wanted with it. Maybe I'll play
> with that too. Could be done with a spline based function, but a limited
> inbuilt should be quite a bit faster.
Have not been able to invest the uninterrupted and focused time to see where the
interpretation of the quilted function went wrong, or any of that.
But with regard to using a bicubic spline, that is how I got my function to
exhibit the "inflection point" that the documentation graphs show (It's just a
flat tangent=0 point). Actually having a function that allowed a true
inflection point would be interesting - then a tile could have a groove around
the edge, like some cutting boards do.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> > William F Pokorny <ano### [at] anonymous net> wrote:
> > William F Pokorny <ano### [at] anonymous org> wrote:
> > This meant the quilt_cubic function was
> > getting an over all range of values from 0 to 0.867.
Yeah, you/I should play around with PREmultiplying that by 1.15....
The implementation seems to me to be a bit unneccesarily Byzantine, and I tried
to keep the original function - but simplify it by multiplying through, and
that's how I got my interpretation of the quilted function wrong.
Your fix is indeed correct.
The part that has (still) got me mystified now is calculating the INPUT to the
quilt_cubic function, as the value function I was using with floor and FLOOR
didn't seem to make any sense. It should be a mirrored function across 0, no?
We discussed this and I think for this application
#declare FLOOR = function (T) {floor (abs(T))}
is the kind of thing that is intended.
So to keep it simple I just do
#declare ValueX = function (X) {abs(X)-floor(abs(X))-0.5}
Then when I run through the calculations stepwise, I get something smooth and
symmetric. (But holy cow - that quilt_cubic function... :O )
Here are the graphs I got when I plotted the original quilted sub-functions in a
daisy-chained stepwise manner (range -0.5 to 0.5) compared with how I originally
did mine (range 0-1).
I _think_ it looks right, given the full black and never fully white values in
the original pattern, but I'm confused about the difference between my SDL
calculations and the full color function {quilted ....} plots I did.
Which means I might still not be evaluating this correctly.
Given that the function {quilted ....} just gives a sort of flattened U, I'm
wondering if there might not be a simpler way to achieve THAT shape, since I
think whatever the (unlabeled) graphs were trying to convey were misleading.
The only other thing I can think of is to use a correcting function - perhaps
that can be enabled with a flag, that way new scenes could use the new or the
old way,
or implemented separately: something like pigment {function {quilted} * function
{quilt_correct}} could be done, so that extant scenes wouldn't have to be
modified at all, but new scenes could add the additional correction in.
The idea is that since there is a variation between the center of an edge and a
corner, a compensating function could be applied to make the whole edge
(reasonably) constant.
It's ugly, but "backward compatibility" always is.
My vote is to come up with a nice clean simple easy-to-understand and document
function has has none of the current problems, looks good on a single unit cube
at a large size, jettison the old code, issue a deprecation warning or "this
version of quilted is a new experimental feature, replacing the original...."
type message, and go from there.
(how many people have actually used quilted in past scenes?) org> wrote:
> > This meant the quilt_cubic function was
> > getting an over all range of values from 0 to 0.867.
Yeah, you/I should play around with PREmultiplying that by 1.15....
The implementation seems to me to be a bit unneccesarily Byzantine, and I tried
to keep the original function - but simplify it by multiplying through, and
that's how I got my interpretation of the quilted function wrong.
Your fix is indeed correct.
The part that has (still) got me mystified now is calculating the INPUT to the
quilt_cubic function, as the value function I was using with floor and FLOOR
didn't seem to make any sense. It should be a mirrored function across 0, no?
We discussed this and I think for this application
#declare FLOOR = function (T) {floor (abs(T))}
is the kind of thing that is intended.
So to keep it simple I just do
#declare ValueX = function (X) {abs(X)-floor(abs(X))-0.5}
Then when I run through the calculations stepwise, I get something smooth and
symmetric. (But holy cow - that quilt_cubic function... :O )
Here are the graphs I got when I plotted the original quilted sub-functions in a
daisy-chained stepwise manner (range -0.5 to 0.5) compared with how I originally
did mine (range 0-1).
I _think_ it looks right, given the full black and never fully white values in
the original pattern, but I'm confused about the difference between my SDL
calculations and the full color function {quilted ....} plots I did.
Which means I might still not be evaluating this correctly.
Given that the function {quilted ....} just gives a sort of flattened U, I'm
wondering if there might not be a simpler way to achieve THAT shape, since I
think whatever the (unlabeled) graphs were trying to convey were misleading.
The only other thing I can think of is to use a correcting function - perhaps
that can be enabled with a flag, that way new scenes could use the new or the
old way,
or implemented separately: something like pigment {function {quilted} * function
{quilt_correct}} could be done, so that extant scenes wouldn't have to be
modified at all, but new scenes could add the additional correction in.
The idea is that since there is a variation between the center of an edge and a
corner, a compensating function could be applied to make the whole edge
(reasonably) constant.
It's ugly, but "backward compatibility" always is.
My vote is to come up with a nice clean simple easy-to-understand and document
function has has none of the current problems, looks good on a single unit cube
at a large size, jettison the old code, issue a deprecation warning or "this
version of quilted is a new experimental feature, replacing the original...."
type message, and go from there.
(how many people have actually used quilted in past scenes?)
Post a reply to this message
Attachments:
Download 'quilted.png' (110 KB)
Preview of image 'quilted.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/18/20 9:34 AM, Bald Eagle wrote:
> William F Pokorny <ano### [at] anonymous org> wrote:
>
>> I keep thrashing around on what to do fix wise with the true quilted
>> normal pattern...
>>
>> One of the weird things with the existing implementation is the x,y,z
>> coordinates in the unit cube are all, always used in a distance from
>> unit cube center calculation. This meant the quilt_cubic function was
>> getting an over all range of values from 0 to 0.867.
>
> Yes. None of the vector components ever exceeded +/-0.5, and so
> sqrt( pow(x,2) + pow(y,2) + pow(z,2) ) =
> sqrt (0.25 + 0.25 + 0.25) =
> sqrt (0.75) =
> 0.866025404
>
> However, you're omitting the fact that the end result of the calculations was
> them multiplied by 1/(sqrt(3/4) = 1.154700538
> and 0.866025404 * 1.154700538 = 1.0
>
Yes. I wasn't clear I was talking about the input range to the
quilt_cubic there. FWIW - the output range actually peaks out at about
1.03 and this one cause of the normal flipping which currently sometimes
happens.
>> However, at any given face position in the unit cube the range of values
>> fed to quilt_cubic was in fact a sub range of the 0 to 0.867 range. At
>> the unit face it was 0.5 to 0.867 (values delta of 0.367). At face
>> positions moving inward toward 0.0 the delta range moved and increased
>> in size (to 0.707 on the floor).
>
Dang, dang, dang... That parenthetical should have read: (to 0.707 at
the mid point between the floor and ceiling).
> Because at N = 0, one of the vector components was always 0, and so the equation
> would then be
> sqrt (0.25 + 0.25 + 0) =
> sqrt (0.5) =
> 0.707106781
>
> This is the reason why in my initial coding, I instead used a function
> incorporating min(max( QX2(x), max(QY2(y), QZ2(z)) ), 0)
> (the equation for an isosurface cube)
>
> The idea of course being that such a method should give a constant 1.0 along the
> entire surface of any given face.
>
Yes, this idea similar to the approach I took with my 2D axis projection
option. I decoupled the other two axises too in running quilt_cubic
twice for each projection. This is the option that looks less quilted
but which is more flexible with respect to effects.
>> We could go a different way for a fix. One which implements the
>> previous, unit cube centered, face results by default, but which now
>> offers an offset keyword. The offset would let users slide a 0.367 delta
>> value range around as fed to the quilt_cubic function. Sort of a left /
>> right slider for the posted quilt_cubic curves. (Back to the function's
>> curves having meaning...)
>
> Not sure where that comes from:
> (0.367.... 0.160? 0.867-0.707?
> 0.866025404−0.707106781 = 0.158918623)
>
The minimum value at any full (+-0.5) face is 0.5. Given the max in the
corners is 0.867 the range is 0.367. (And why did I use 0.867 - it
really is 0.866...)
>
>> This offset keyword would allow users having existing scenes at face
>> positions not on the full unit cube to achieve a previous result (in
>> conjunction with bump magnitude) - at least where it wasn't previously
>> some corrupt, partly inverted result.
>
> Since I got lost and I don't understand, this would be something different that
> simply translating the pigment pattern by some amount would _not_ fix?
Yes.
Likely my miss-step on the parenthetical comment didn't help you - or
anyone understand. Remember too. I'm talking 'only' about the true
normal implementation.
Well lying a little, I might occasionally make mention of the "value for
map" form , but with povr I plan to drop the value based version of the
pattern for normal maps, pigment maps whatever. I've not spent a lot of
time with that method though some time with possible replacements.
>
>> Aside: The thrashing here gets back to an early question of Bald
>> Eagle's. Why not calculate 0-1 face input values for a Bezier curve
>> where the user specifies both end points in addition to the control
>> points. It looks to me like this was closer to the form of the original
>> internal equation; later simplified.
>
> I'm still confused about a number of points, the most basic and direct is the
> graphing of the internal quilted function results vs the documentation graphs.
>
I don't know what was up with those graphs either. They do not really
line up directly with what's actually going on that I can see.
Let me grab a cup of coffee and review the value for map version again.
I'll still delete the quilted value pattern for povr, but thinking now
maybe I will create an f_quilted() or F_quilted() inbuilt with a forced
x,y oz z axis specification. Or maybe an F_quilted() similar to F_dents().
Anyway. What's there for the 'value for map' quilted is really a
quilt_cubic() shaped spherical pattern. One where the user doesn't
really know the input values for quilt_cubic() or the response curves
given the control values...
>> Today suppose, that form of 'quilted_cubic' would better be an inbuilt
>> function. Users could do what ever they wanted with it. Maybe I'll play
>> with that too. Could be done with a spline based function, but a limited
>> inbuilt should be quite a bit faster.
>
> Have not been able to invest the uninterrupted and focused time to see where the
> interpretation of the quilted function went wrong, or any of that.
>
> But with regard to using a bicubic spline, that is how I got my function to
> exhibit the "inflection point" that the documentation graphs show (It's just a
> flat tangent=0 point). Actually having a function that allowed a true
> inflection point would be interesting - then a tile could have a groove around
> the edge, like some cutting boards do.
>
Yes, something with more control might be good too, but when I start to
think of complex patterns, I start to think those best left to user
functions.
----------
Let me read your second post from yesterday on this topic.
> Yeah, you/I should play around with PREmultiplying that by 1.15....
Yes, normalizing the input to a 0-0.5 or 0-1 range in some fashion an
option.
However, I've played with this a little with this idea for the true
normal version. To my eye the results don't look as good or varied as
partial ranges. In fact I wonder if the sub range positioning might have
been left as it is because the quilt_cubic output functions differ more
over the range 0.5-0.866 for any given set of input control points.
> We discussed this and I think for this application
> #declare FLOOR = function (T) {floor (abs(T))}
> is the kind of thing that is intended.
>
> So to keep it simple I just do
> #declare ValueX = function (X) {abs(X)-floor(abs(X))-0.5}
Agree and this would I believe be one approach to eliminating the
negative axis value bias problem of the original. But passing the major
normal axis through or forcing the selection of the major axis and using
just the other two coordinates works too and this what my approaches
currently do.
> Given that the function {quilted ....} just gives a sort of
> flattened U, I'm wondering if there might not be a simpler way
> to achieve THAT shape, since I think whatever the (unlabeled)
> graphs were trying to convey were misleading.
Yes, likely. In povr we have another quilted option in the inbuilt
f_agate() if you remember but one where the "stitch" is always V shaped
(as are most of today's actual quilted results if we're honest).
----
Lastly, some extremely subtle and obscure pondering/rambling. The wave
shaping code for patterns of the 'value for map variety' was added at
some point in time. Further negative values flip "by code comments at
least" was added at some point in time.
The value quilted is also special in the <=v3.8 code in having a default
frequency setting of 0.0. You will still see the value and floor flip:
if(value < 0.0)
value -= floor(value);
in the wave shaping code.
For one this means you cannot plot unmodified pattern code output with:
#declare Q = function {pigment {quilted control0 c0 control1 CN[c1]}}
or
#declare Q = function {pattern {...}
or
#declare Q = function {pigment_pattern {...}
though for quilted the result is closer than most due the default
freq==0. The pigment_pattern version is also more complicated because
many patterns have default color maps and that versions uses a
conversion to grey scale to come up with the function 'value.' Always
use an explicit 0-1 color map with mainstream POV-Ray if you want 0-1
values.
The povr branch has eliminated all non block pattern default color maps
- so coding function { pigment_pattern { whatever-not_block-type}} is
safe - you get 0-1 as the default color map.
Povr also has an explicit raw_wave keyword which lets you see and plot
the full pattern return values(1) directly.
(1) - Some pattern code - and the function {} pattern path had it's own
varied clamping which has also been removed in povr where it made sense
to remove it. With tiling patterns the tiling clamping is still there
for example.
SO! Point is, avoid making conclusions about internal code behavior with
<=v3.8 pattern / pigment plotting code - unless you REALLY understand it
and keep it all in mind. It's a tangle.
The pondering part. I wonder if changes over time in this tangle of
pattern treatments led to those c0, c1 plots somehow. Perhaps at some
point they did reflect the pattern value version.
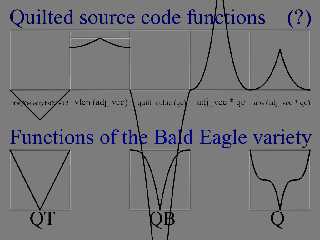
I can look over your QT, QB -> Q version as part of the quilted mix if
you want to send them along. The original version of the quilt_cubic had
N0, N1 parameters which basically let one specify the Y values at x=0
and x=1.0. I've extended that in an inbuilt playpen function to allow me
to set the x values to other than 0 or 1. After which it starts to look
more like a bezier segment result where only the y control values can be
set and the x control postions are fixed. See attached image. Off to see
if I can find my old bezier segment code.
Bill P. org> wrote:
>
>> I keep thrashing around on what to do fix wise with the true quilted
>> normal pattern...
>>
>> One of the weird things with the existing implementation is the x,y,z
>> coordinates in the unit cube are all, always used in a distance from
>> unit cube center calculation. This meant the quilt_cubic function was
>> getting an over all range of values from 0 to 0.867.
>
> Yes. None of the vector components ever exceeded +/-0.5, and so
> sqrt( pow(x,2) + pow(y,2) + pow(z,2) ) =
> sqrt (0.25 + 0.25 + 0.25) =
> sqrt (0.75) =
> 0.866025404
>
> However, you're omitting the fact that the end result of the calculations was
> them multiplied by 1/(sqrt(3/4) = 1.154700538
> and 0.866025404 * 1.154700538 = 1.0
>
Yes. I wasn't clear I was talking about the input range to the
quilt_cubic there. FWIW - the output range actually peaks out at about
1.03 and this one cause of the normal flipping which currently sometimes
happens.
>> However, at any given face position in the unit cube the range of values
>> fed to quilt_cubic was in fact a sub range of the 0 to 0.867 range. At
>> the unit face it was 0.5 to 0.867 (values delta of 0.367). At face
>> positions moving inward toward 0.0 the delta range moved and increased
>> in size (to 0.707 on the floor).
>
Dang, dang, dang... That parenthetical should have read: (to 0.707 at
the mid point between the floor and ceiling).
> Because at N = 0, one of the vector components was always 0, and so the equation
> would then be
> sqrt (0.25 + 0.25 + 0) =
> sqrt (0.5) =
> 0.707106781
>
> This is the reason why in my initial coding, I instead used a function
> incorporating min(max( QX2(x), max(QY2(y), QZ2(z)) ), 0)
> (the equation for an isosurface cube)
>
> The idea of course being that such a method should give a constant 1.0 along the
> entire surface of any given face.
>
Yes, this idea similar to the approach I took with my 2D axis projection
option. I decoupled the other two axises too in running quilt_cubic
twice for each projection. This is the option that looks less quilted
but which is more flexible with respect to effects.
>> We could go a different way for a fix. One which implements the
>> previous, unit cube centered, face results by default, but which now
>> offers an offset keyword. The offset would let users slide a 0.367 delta
>> value range around as fed to the quilt_cubic function. Sort of a left /
>> right slider for the posted quilt_cubic curves. (Back to the function's
>> curves having meaning...)
>
> Not sure where that comes from:
> (0.367.... 0.160? 0.867-0.707?
> 0.866025404−0.707106781 = 0.158918623)
>
The minimum value at any full (+-0.5) face is 0.5. Given the max in the
corners is 0.867 the range is 0.367. (And why did I use 0.867 - it
really is 0.866...)
>
>> This offset keyword would allow users having existing scenes at face
>> positions not on the full unit cube to achieve a previous result (in
>> conjunction with bump magnitude) - at least where it wasn't previously
>> some corrupt, partly inverted result.
>
> Since I got lost and I don't understand, this would be something different that
> simply translating the pigment pattern by some amount would _not_ fix?
Yes.
Likely my miss-step on the parenthetical comment didn't help you - or
anyone understand. Remember too. I'm talking 'only' about the true
normal implementation.
Well lying a little, I might occasionally make mention of the "value for
map" form , but with povr I plan to drop the value based version of the
pattern for normal maps, pigment maps whatever. I've not spent a lot of
time with that method though some time with possible replacements.
>
>> Aside: The thrashing here gets back to an early question of Bald
>> Eagle's. Why not calculate 0-1 face input values for a Bezier curve
>> where the user specifies both end points in addition to the control
>> points. It looks to me like this was closer to the form of the original
>> internal equation; later simplified.
>
> I'm still confused about a number of points, the most basic and direct is the
> graphing of the internal quilted function results vs the documentation graphs.
>
I don't know what was up with those graphs either. They do not really
line up directly with what's actually going on that I can see.
Let me grab a cup of coffee and review the value for map version again.
I'll still delete the quilted value pattern for povr, but thinking now
maybe I will create an f_quilted() or F_quilted() inbuilt with a forced
x,y oz z axis specification. Or maybe an F_quilted() similar to F_dents().
Anyway. What's there for the 'value for map' quilted is really a
quilt_cubic() shaped spherical pattern. One where the user doesn't
really know the input values for quilt_cubic() or the response curves
given the control values...
>> Today suppose, that form of 'quilted_cubic' would better be an inbuilt
>> function. Users could do what ever they wanted with it. Maybe I'll play
>> with that too. Could be done with a spline based function, but a limited
>> inbuilt should be quite a bit faster.
>
> Have not been able to invest the uninterrupted and focused time to see where the
> interpretation of the quilted function went wrong, or any of that.
>
> But with regard to using a bicubic spline, that is how I got my function to
> exhibit the "inflection point" that the documentation graphs show (It's just a
> flat tangent=0 point). Actually having a function that allowed a true
> inflection point would be interesting - then a tile could have a groove around
> the edge, like some cutting boards do.
>
Yes, something with more control might be good too, but when I start to
think of complex patterns, I start to think those best left to user
functions.
----------
Let me read your second post from yesterday on this topic.
> Yeah, you/I should play around with PREmultiplying that by 1.15....
Yes, normalizing the input to a 0-0.5 or 0-1 range in some fashion an
option.
However, I've played with this a little with this idea for the true
normal version. To my eye the results don't look as good or varied as
partial ranges. In fact I wonder if the sub range positioning might have
been left as it is because the quilt_cubic output functions differ more
over the range 0.5-0.866 for any given set of input control points.
> We discussed this and I think for this application
> #declare FLOOR = function (T) {floor (abs(T))}
> is the kind of thing that is intended.
>
> So to keep it simple I just do
> #declare ValueX = function (X) {abs(X)-floor(abs(X))-0.5}
Agree and this would I believe be one approach to eliminating the
negative axis value bias problem of the original. But passing the major
normal axis through or forcing the selection of the major axis and using
just the other two coordinates works too and this what my approaches
currently do.
> Given that the function {quilted ....} just gives a sort of
> flattened U, I'm wondering if there might not be a simpler way
> to achieve THAT shape, since I think whatever the (unlabeled)
> graphs were trying to convey were misleading.
Yes, likely. In povr we have another quilted option in the inbuilt
f_agate() if you remember but one where the "stitch" is always V shaped
(as are most of today's actual quilted results if we're honest).
----
Lastly, some extremely subtle and obscure pondering/rambling. The wave
shaping code for patterns of the 'value for map variety' was added at
some point in time. Further negative values flip "by code comments at
least" was added at some point in time.
The value quilted is also special in the <=v3.8 code in having a default
frequency setting of 0.0. You will still see the value and floor flip:
if(value < 0.0)
value -= floor(value);
in the wave shaping code.
For one this means you cannot plot unmodified pattern code output with:
#declare Q = function {pigment {quilted control0 c0 control1 CN[c1]}}
or
#declare Q = function {pattern {...}
or
#declare Q = function {pigment_pattern {...}
though for quilted the result is closer than most due the default
freq==0. The pigment_pattern version is also more complicated because
many patterns have default color maps and that versions uses a
conversion to grey scale to come up with the function 'value.' Always
use an explicit 0-1 color map with mainstream POV-Ray if you want 0-1
values.
The povr branch has eliminated all non block pattern default color maps
- so coding function { pigment_pattern { whatever-not_block-type}} is
safe - you get 0-1 as the default color map.
Povr also has an explicit raw_wave keyword which lets you see and plot
the full pattern return values(1) directly.
(1) - Some pattern code - and the function {} pattern path had it's own
varied clamping which has also been removed in povr where it made sense
to remove it. With tiling patterns the tiling clamping is still there
for example.
SO! Point is, avoid making conclusions about internal code behavior with
<=v3.8 pattern / pigment plotting code - unless you REALLY understand it
and keep it all in mind. It's a tangle.
The pondering part. I wonder if changes over time in this tangle of
pattern treatments led to those c0, c1 plots somehow. Perhaps at some
point they did reflect the pattern value version.
I can look over your QT, QB -> Q version as part of the quilted mix if
you want to send them along. The original version of the quilt_cubic had
N0, N1 parameters which basically let one specify the Y values at x=0
and x=1.0. I've extended that in an inbuilt playpen function to allow me
to set the x values to other than 0 or 1. After which it starts to look
more like a bezier segment result where only the y control values can be
set and the x control postions are fixed. See attached image. Off to see
if I can find my old bezier segment code.
Bill P.
Post a reply to this message
Attachments:
Download 'playpen.png' (153 KB)
Preview of image 'playpen.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 10/18/20 6:10 AM, William F Pokorny wrote:
> On 10/17/20 10:49 PM, Kenneth wrote:
....
>
> We could go a different way for a fix. One which implements the
> previous, unit cube centered, face results by default, but which now
> offers an offset keyword. The offset would let users slide a 0.367 delta
> value range around as fed to the quilt_cubic function. Sort of a left /
> right slider for the posted quilt_cubic curves. (Back to the function's
> curves having meaning...)
>
> Attached is a second image quiltedOptionTwo.png. The left set of 9 is
> the same A to I set. Here it's what users would see at the unit faces
> with the existing implementation (ignoring the noise issue). The offset
> is 0.5 for these. In the right set of 9, I've used an offset of -1.0.
> Many of the faces invert (inside of the pillow) and the results are more
> pillow like.
>
> Is this a better way to go for a fix?
>
I going to use this option as a fix for the true normal version of
quilted in povr - without the offset keyword for now.
Plan is to enable more complicated alternatives as functions. Maybe the
earlier more flexible but less quilted / pillow like alternative as
another true normal pattern at some point.
Attached is an image showing part of the current biscuit.pov scene which
is one commonly run; It's the 'make check' test scene. On the left the
current v3.8 result. In the middle the with the fix. On the right the
difference.
Because the evaluation point drifts around due turbulence, the v3.8
quilted is showing both the issue of varying strengths in the quilting
and partial inversions (sudden changes in intensity along a curve).
Aside: One other subtle issue I should mention with the current and
longstanding code and only partly addressed with the update. Larger,
(especially negative) bump sizes can cause inversions to face the away
from the primary incoming normal for the ray (black areas). This can
always happen, but is more likely with no_bump_scale(1). Yes, it's
possible to add code to prevent this(2), but the current fix is already
adding +6%, give or take, to the run time of biscuit.pov. Plus, this
exposure is more general than quilted.
(1) - Probably a the reason for 0.5 the default bump size. Staying <<1
is more stable.
(2) - My thinking is ideally normal perturbations don't completely
invert the normal. Meaning the major inside/outside surface ray ->
normal relation stays the same (doesn't suddenly act as shadowed).
Bill P.
Post a reply to this message
Attachments:
Download 'qlt_biscuit_v38_to_biscuit.jpg' (116 KB)
Preview of image 'qlt_biscuit_v38_to_biscuit.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
FYI:
I was just digging around in the source code for the older versions, looking for
some information on normal calculations, and there is a comment that the quilted
normal was written by Dan farmer in 1994.
- BE
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Just so people know, there is no limit to how people will take advantage of your
curiosity and labor.
"Freya" (Joachim) Holmer has a very popular youtube video.
No one can possibly guess where the inspiration for that one came from.
Rodolphe Vaillant
This is not the "March 18" version, but one that was recently updated without
attribution between this past Friday 2025-11-21 and today.
https://rodolphe-vaillant.fr/entry/87/normal-to-an-implicit-surface
Curious update with no email. We'll see how this one plays out.
"Keep your friends close, keep your enemies closer."
"There is no honor amongst thieves."
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
"Bald Eagle" <cre### [at] netscape net> wrote:
> Just so people know, there is no limit to how people will take advantage of your
> curiosity and labor.
> ...
> "There is no honor amongst thieves."
imitation is the sincerest form of flattery (that mediocrity can pay to
greatness) ?
(Google says I'm quoting Oscar Wilde)
regards, jr. net> wrote:
> Just so people know, there is no limit to how people will take advantage of your
> curiosity and labor.
> ...
> "There is no honor amongst thieves."
imitation is the sincerest form of flattery (that mediocrity can pay to
greatness) ?
(Google says I'm quoting Oscar Wilde)
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"jr" <cre### [at] gmail com> wrote:
> imitation is the sincerest form of flattery (that mediocrity can pay to
> greatness) ?
"(you) can resist everything except temptation" ;) :P com> wrote:
> imitation is the sincerest form of flattery (that mediocrity can pay to
> greatness) ?
"(you) can resist everything except temptation" ;) :P
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()