 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 01.08.2016 17:51, Le_Forgeron wrote:
> for the time being, what I called "nurbs" object is actually a
non-uniform-rational-bezier :
> * the order of the rational B-spline is the number of control point (it's an implict
value), so actually that a ration Bezier.
Thanks for the clarification that makes sense.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> Le 01/08/2016 à 11:08, Mr a écrit :
> > At one point, Blender NURBS were implemented from an external open source
> > library : libNurbana
> > https://sourceforge.net/projects/nurbana/?source=directory
> > Don't know if it's still the case.
>
> thanks for the link, I will have a look later.
A blender dev told me it's no longer the case, the Blender NURBS code is now
specific. but both code sources are probably good references. fr> wrote:
> Le 01/08/2016 à 11:08, Mr a écrit :
> > At one point, Blender NURBS were implemented from an external open source
> > library : libNurbana
> > https://sourceforge.net/projects/nurbana/?source=directory
> > Don't know if it's still the case.
>
> thanks for the link, I will have a look later.
A blender dev told me it's no longer the case, the Blender NURBS code is now
specific. but both code sources are probably good references.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> Thanks for that code, but the computed normal is an approximation, not the real
value.
>
> It's like computing the derivative of a polynomial expression by sampling values
around the point of interest, instea
d of actually performing the derivation of the equation: you get an approximated
value, but no formula.
polynom bernstein no? fr> wrote:
> Thanks for that code, but the computed normal is an approximation, not the real
value.
>
> It's like computing the derivative of a polynomial expression by sampling values
around the point of interest, instea
d of actually performing the derivation of the equation: you get an approximated
value, but no formula.
polynom bernstein no?
Post a reply to this message
Attachments:
Download 'beziermesh.java.txt' (10 KB)
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 30/07/2016 à 13:13, LanuHum a écrit :
> Le_Forgeron <jgr### [at] free fr> wrote:
>
>> I would need a few more round tuits and my stock is low.
>
> :))))))
> And who is now easy to live?
>
>
>
A bit of progress.
The number on the image is the order (aka degree+1) of the curve used in the Nurbs.
I hope you are ready to handle the knot vectors, because I gave up the
user-friendliness of opened/clamped/closed
nu7 is similar to the rational bezier that was previously available. (because with 7
control points, at order 7, the nurbs (with the knot vectors that were provided) is a
single rational bezier)
nu3 is more similar to your provided picture, or it could be nu4.
Still to do: implement the computation of normal (I found a nice formula, but I lack
the time to code it), not used so far.
Also attached is the SDL scene with what is the equivalent of Jar-Jar in front of the
Chamber:
I do not know yet who is Palpatine, but there is a big step towards the dark side of
the Force.
Because the nurbs is transformed into a mesh (in the SDL so far). fr> wrote:
>
>> I would need a few more round tuits and my stock is low.
>
> :))))))
> And who is now easy to live?
>
>
>
A bit of progress.
The number on the image is the order (aka degree+1) of the curve used in the Nurbs.
I hope you are ready to handle the knot vectors, because I gave up the
user-friendliness of opened/clamped/closed
nu7 is similar to the rational bezier that was previously available. (because with 7
control points, at order 7, the nurbs (with the knot vectors that were provided) is a
single rational bezier)
nu3 is more similar to your provided picture, or it could be nu4.
Still to do: implement the computation of normal (I found a nice formula, but I lack
the time to code it), not used so far.
Also attached is the SDL scene with what is the equivalent of Jar-Jar in front of the
Chamber:
I do not know yet who is Palpatine, but there is a big step towards the dark side of
the Force.
Because the nurbs is transformed into a mesh (in the SDL so far).
Post a reply to this message
Attachments:
Download 'nu7.png' (40 KB)
Download 'nu6.png' (43 KB)
Download 'nu5.png' (45 KB)
Download 'nu4.png' (47 KB)
Download 'nu3.png' (56 KB)
Download 'nu2.png' (79 KB)
Download 'nurbsmesh.inc.txt' (2 KB)
Download 'nu.pov.txt' (4 KB)
Preview of image 'nu7.png'

Preview of image 'nu6.png'

Preview of image 'nu5.png'

Preview of image 'nu4.png'

Preview of image 'nu3.png'

Preview of image 'nu2.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
>
> Also attached is the SDL scene with what is the equivalent of Jar-Jar in front of
the Chamber:
> I do not know yet who is Palpatine, but there is a big step towards the dark side of
the Force.
>
Deep Purple:
Child in time
"Sweet child in time
You'll see the line
The line that's drawn between
Good and bad
See the blind man
Shooting at the world
Bullets flying
Ohh taking toll
If you've been bad
Oh Lord I bet you have
And you've not been hit
Oh by flying lead
You'd better close your eyes
Ooohhhh bow your head
Wait for the ricochet"
> Because the nurbs is transformed into a mesh (in the SDL so far).
In the universe there are objects with sharp corners. I'm glad you saw them.
:))))))))) fr> wrote:
>
> Also attached is the SDL scene with what is the equivalent of Jar-Jar in front of
the Chamber:
> I do not know yet who is Palpatine, but there is a big step towards the dark side of
the Force.
>
Deep Purple:
Child in time
"Sweet child in time
You'll see the line
The line that's drawn between
Good and bad
See the blind man
Shooting at the world
Bullets flying
Ohh taking toll
If you've been bad
Oh Lord I bet you have
And you've not been hit
Oh by flying lead
You'd better close your eyes
Ooohhhh bow your head
Wait for the ricochet"
> Because the nurbs is transformed into a mesh (in the SDL so far).
In the universe there are objects with sharp corners. I'm glad you saw them.
:)))))))))
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
#declare ORDER=clock;
#declare DEN=8-ORDER;
#declare OBJE=
nurbs {ORDER,ORDER,7,7,
#for(C,0,1,1)
#for(B,1,ORDER-1,1)
0,
#end
#for(A,0,1,1/DEN)
A,
#end
#for(B,1,ORDER-1,1)
if u != v ???
if nurbs{3,9,3,9} ???
Error.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 04/09/2016 à 20:16, LanuHum a écrit :
> #declare ORDER=clock;
> #declare DEN=8-ORDER;
> #declare OBJE=
> nurbs {ORDER,ORDER,7,7,
> #for(C,0,1,1)
> #for(B,1,ORDER-1,1)
> 0,
> #end
> #for(A,0,1,1/DEN)
> A,
> #end
> #for(B,1,ORDER-1,1)
>
>
> if u != v ???
> if nurbs{3,9,3,9} ???
> Error.
>
>
>
Of course "error", That part describes the know vector for each direction.
What did you expect ?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> Le 04/09/2016 à 20:16, LanuHum a écrit :
> > #declare ORDER=clock;
> > #declare DEN=8-ORDER;
> > #declare OBJE=
> > nurbs {ORDER,ORDER,7,7,
> > #for(C,0,1,1)
> > #for(B,1,ORDER-1,1)
> > 0,
> > #end
> > #for(A,0,1,1/DEN)
> > A,
> > #end
> > #for(B,1,ORDER-1,1)
> >
> >
> > if u != v ???
> > if nurbs{3,9,3,9} ???
> > Error.
> >
> >
> >
>
> Of course "error", That part describes the know vector for each direction.
> What did you expect ?
I was expecting a rational decision. If the length is 1000, and the width is
0.1. Why do I need the same division? fr> wrote:
> Le 04/09/2016 à 20:16, LanuHum a écrit :
> > #declare ORDER=clock;
> > #declare DEN=8-ORDER;
> > #declare OBJE=
> > nurbs {ORDER,ORDER,7,7,
> > #for(C,0,1,1)
> > #for(B,1,ORDER-1,1)
> > 0,
> > #end
> > #for(A,0,1,1/DEN)
> > A,
> > #end
> > #for(B,1,ORDER-1,1)
> >
> >
> > if u != v ???
> > if nurbs{3,9,3,9} ???
> > Error.
> >
> >
> >
>
> Of course "error", That part describes the know vector for each direction.
> What did you expect ?
I was expecting a rational decision. If the length is 1000, and the width is
0.1. Why do I need the same division?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 04/09/2016 à 21:47, LanuHum a écrit :
> Le_Forgeron <jgr### [at] free fr> wrote:
>> Le 04/09/2016 à 20:16, LanuHum a écrit :
>>> #declare ORDER=clock;
>>> #declare DEN=8-ORDER;
>>> #declare OBJE=
>>> nurbs {ORDER,ORDER,7,7,
>>> #for(C,0,1,1)
>>> #for(B,1,ORDER-1,1)
>>> 0,
>>> #end
>>> #for(A,0,1,1/DEN)
>>> A,
>>> #end
>>> #for(B,1,ORDER-1,1)
>>>
>>>
>>> if u != v ???
>>> if nurbs{3,9,3,9} ???
>>> Error.
>>>
>>>
>>>
>>
>> Of course "error", That part describes the know vector for each direction.
>> What did you expect ?
>
> I was expecting a rational decision. If the length is 1000, and the width is
> 0.1. Why do I need the same division?
This is SDL. It was used for that nurbs to generate the knot vectors.
You can use whatever knot vectors you want (as long as valid for knot
vector).
I won't explain knot vectors. fr> wrote:
>> Le 04/09/2016 à 20:16, LanuHum a écrit :
>>> #declare ORDER=clock;
>>> #declare DEN=8-ORDER;
>>> #declare OBJE=
>>> nurbs {ORDER,ORDER,7,7,
>>> #for(C,0,1,1)
>>> #for(B,1,ORDER-1,1)
>>> 0,
>>> #end
>>> #for(A,0,1,1/DEN)
>>> A,
>>> #end
>>> #for(B,1,ORDER-1,1)
>>>
>>>
>>> if u != v ???
>>> if nurbs{3,9,3,9} ???
>>> Error.
>>>
>>>
>>>
>>
>> Of course "error", That part describes the know vector for each direction.
>> What did you expect ?
>
> I was expecting a rational decision. If the length is 1000, and the width is
> 0.1. Why do I need the same division?
This is SDL. It was used for that nurbs to generate the knot vectors.
You can use whatever knot vectors you want (as long as valid for knot
vector).
I won't explain knot vectors.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
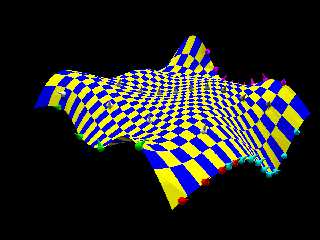
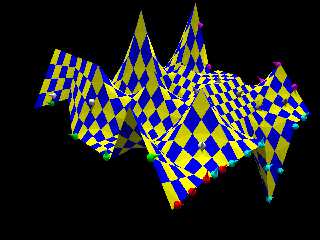
Le 26/07/2016 à 19:06, Nekar Xenos a écrit :
> Yay, NURBS!
And now with normal computation too, in Hgpovray (branch Hgpovray of
https://github.com/LeForgeron/povray.git ), if someone ever need it
(what is a smooth_triangle ?)
That should finish that nurbs part... oh wait, documentation is still
not done... Winter is coming.
Post a reply to this message
Attachments:
Download 'nu.pov.txt' (6 KB)
Download 'nu5.png' (161 KB)
Download 'nu4.png' (184 KB)
Download 'nu3.png' (189 KB)
Download 'nu2.png' (198 KB)
Download 'nu1.png' (217 KB)
Download 'nu0.png' (217 KB)
Preview of image 'nu5.png'

Preview of image 'nu4.png'

Preview of image 'nu3.png'
Preview of image 'nu2.png'

Preview of image 'nu1.png'

Preview of image 'nu0.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()