 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
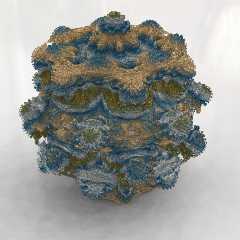
Here's my latest Mandelbulb, rendered using the isosurface / df3 method.
but no radiosity: it was just too slow. This render took over 7 days on my
480MHz machine. I was hoping for a more impressive looking result, after all
that render time. Oh well.
Post a reply to this message
Attachments:
Download 'mandelbulbja0s90.jpg' (124 KB)
Preview of image 'mandelbulbja0s90.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"PM 2Ring" <nomail@nomail> schreef in bericht
news:web.4b247f29ce81d185f4c648ed0@news.povray.org...
> Here's my latest Mandelbulb, rendered using the isosurface / df3 method.
> sources,
> but no radiosity: it was just too slow. This render took over 7 days on my
> 480MHz machine. I was hoping for a more impressive looking result, after
> all
> that render time. Oh well.
I do find it pretty impressive. Reminds me of some kind of delicate
porcelaine vase. The absence of shadows increases that feeling. I am
impressed by your patience too ;)
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Thomas de Groot" <tDOTdegroot@interDOTnlANOTHERDOTnet> wrote:
> I do find it pretty impressive. Reminds me of some kind of delicate
> porcelaine vase. The absence of shadows increases that feeling. I am
> impressed by your patience too ;)
Thanks, Thomas. I think my next Mandelbulb renders will be close-ups rather than
trying to do the whole thing. And I might compromise & use a mesh instead of the
isosurface. These complex objects take up so much memory, I couldn't really do
much else while rendering, or the machine would start using virtual memory. That
would've taken months!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
PM 2Ring wrote:
> Here's my latest Mandelbulb, rendered using the isosurface / df3 method.
> but no radiosity: it was just too slow. This render took over 7 days on my
> 480MHz machine. I was hoping for a more impressive looking result, after all
> that render time. Oh well.
>
>
>
>
> ------------------------------------------------------------------------
>
Nice.
Here's a 800^3 isosurface/df3, with radiosity and real HDRI, but I can't
figure out what's wrong with my code, since the shape isn't right. It
was supposed to be the n=8 shape from <-1.2,-1.2,-1.2> to <1.2,1.2,1.2>.
Time: 26 minutes with max_gradient 200 on a 2.6 GHz quad-core (AMD
Phenom 9950) for the render, and somewhere around there for the
generation on an older dual-core linux box.
Here's my c++ code for the iterations if anyone can figure out what is
wrong, I've gone through it many times and can't figure out what's not
right...
Chris
--------------------------------------------------------------------------
/* Iterates the formula at a given x,y,z and returns the smoothed number
of iterations used */
float IteratePoint(double cx, double cy, double cz, double n, double
bailout, int maxiter){
double x=0.0,y=0.0,z=0.0;
double r=0.0,rn=0.0,phin,thetan,sinthetan;
for(int i=0;i<maxiter;i++){
r=sqrt(pow(x,2)+pow(y,2)+pow(z,2));
if(r>bailout){
rn=pow(r,n);
thetan=atan2(sqrt(pow(x,2)+pow(y,2)),z)*n;
phin=atan2(y,z)*n;
x=rn*sin(thetan)*cos(phin)+cx;
y=rn*sin(thetan)*sin(phin)+cy;
z=rn*cos(thetan)+cz;
r=sqrt(pow(x,2)+pow(y,2)+pow(z,2));
return (float)i + 1 - (log(log(r)/log(bailout)))/log(n);
}
rn=pow(r,n);
thetan=atan2(sqrt(pow(x,2)+pow(y,2)),z)*n;
phin=atan2(y,z)*n;
x=rn*sin(thetan)*cos(phin)+cx;
y=rn*sin(thetan)*sin(phin)+cy;
z=rn*cos(thetan)+cz;
}
return (float)maxiter;
}
-------------------
and the loop part : (xs/xe are x-start, x-end values, same for y and z)
for (i=0;i<nx;i++){
for (j=0;j<ny;j++){
#pragma omp parallel
shared(df3,nx,ny,nz,xs,xe,ys,ye,zs,ze,bailout,maxiter,n,i,j,chunk)
private(k,cx,cy,cz)
{
#pragma omp for schedule(dynamic,chunk) nowait
for (k=0;k<nz;k++){
cx = (((double)i+0.5)/(double)nx)*(xe-xs)+xs;
cy = (((double)j+0.5)/(double)ny)*(ye-ys)+ys;
cz = (((double)k+0.5)/(double)nz)*(ze-zs)+zs;
df3[i][j][k]=IteratePoint(cx,cy,cz,n,bailout,maxiter);
}
}
if(j%2==0)
ShowStatus(i*nx+j,nx*ny,"Iterating Fractal: ");
}
}
Post a reply to this message
Attachments:
Download 'mandel_df3.jpg' (69 KB)
Preview of image 'mandel_df3.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
CShake wrote:
[...]
> return (float)i + 1 - (log(log(r)/log(bailout)))/log(n);
[...]
You're return value may be a bit off. The function log(r)/log(bailout) is the
base bailout logarithm of r,* which may not be what you intended. The usual
formulation of this part is the (base n log of the natural log of the bailout)
minus (the base n log of natural log of the radius), where n is the power of the
mandelbulb. This can then be simplified a little.
return (float)i + 1 - ( log(log(bailout))-log(log(r)) )/log(n)
//then
return (float)i + 1 - log(log(bailout)/log(r)) / log(n)
(Somebody check my math, please. This might be simplified a bit more using the
root/log relationships...)
I don't know if this is the root of your current problem; the formulation you're
using may be just fine. I would like to test it, since I've been monkeying with
continuous return values for the last couple of weeks, but won't be able to do
much more on this until after finals.
* http://en.wikipedia.org/wiki/Logarithms#Change_of_base
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
waggy wrote:
> CShake wrote:
> [...]
>> return (float)i + 1 - (log(log(r)/log(bailout)))/log(n);
> [...]
>
> You're return value may be a bit off. The function log(r)/log(bailout) is the
> base bailout logarithm of r,* which may not be what you intended. The usual
> formulation of this part is the (base n log of the natural log of the bailout)
> minus (the base n log of natural log of the radius), where n is the power of the
> mandelbulb. This can then be simplified a little.
>
> return (float)i + 1 - ( log(log(bailout))-log(log(r)) )/log(n)
> //then
> return (float)i + 1 - log(log(bailout)/log(r)) / log(n)
I spent a bit of time on that problem too, and ended up with my equation
based on the Escape Time Algorithm as presented at:
http://en.wikipedia.org/wiki/Mandelbrot_set#Continuous_.28smooth.29_coloring
Unless I'm reading it wrong, that formula is effectively ( i - log[base
N](log[base bailout](r))), which is what I'm using. I assumed that in
the formula on wiki that the inner log (hardcoded as base 2) is actually
base 'bailout', where most formulations of the mandelbrot equation use 2
as the bailout value. The Zn value is stated as the value after n
iterations, which in this case is r. Either I interpreted that equation
wrong, or I'm erroneous in applying the '2d' equation in '3d'.
However, I don't think that's the problem in my equations, since I still
get the same basic shape if I return 'i' instead of the 'smooth'
coloring. Also, I wouldn't expect it to completely remove some of the
features if I got this part of it wrong.
Chris
(I'm also between class and finals, this is how I'm procrastinating
instead of studying and grading a pile of lab reports... )
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
CShake wrote:
> I spent a bit of time on that problem too, and ended up with my equation
> based on the Escape Time Algorithm as presented at:
> http://en.wikipedia.org/wiki/Mandelbrot_set#Continuous_.28smooth.29_coloring
I'm an idiot, please note that I mean 'Normalized Iteration Count
Algorithm' instead of Escape Time in that sentence.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
CShake wrote:
[...]
> phin=atan2(y,z)*n;
[...]
> phin=atan2(y,z)*n;
[...]
Hmm. Perhaps these have a small error? I think maybe they should be like this.
phin=atan2(y,x)*n;
http://www.skytopia.com/project/fractal/2mandelbulb.html#formula
Also, I used the same starting point, then grabbed one of the wikipedia
references and read some more. (I also think I found a small improvement and
plan to write it up over the break.)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"PM 2Ring" wrote:
> Here's my latest Mandelbulb, rendered using the isosurface / df3 method.
> but no radiosity: it was just too slow. This render took over 7 days on my
> 480MHz machine. I was hoping for a more impressive looking result, after all
> that render time. Oh well.
I like your color scheme, and also find the surface can have a nice, porcelain
look with the right finish.
Did you leave Jitter on? Jitter on is the default, but I've found using -J
helps reduce "smearing" and "fuzzing" in the final image.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
waggy wrote:
> CShake wrote:
> [...]
>> phin=atan2(y,z)*n;
> [...]
>> phin=atan2(y,z)*n;
> [...]
>
> Hmm. Perhaps these have a small error? I think maybe they should be like this.
>
> phin=atan2(y,x)*n;
>
> http://www.skytopia.com/project/fractal/2mandelbulb.html#formula
>
> Also, I used the same starting point, then grabbed one of the wikipedia
> references and read some more. (I also think I found a small improvement and
> plan to write it up over the break.)
>
Right you are, once again one character causes all the problem... Thanks!
That fixed code takes a bit longer to run, but all told this image took
less than an hour, 800^3, n=8.0, radiosity, and the media halo uses the
same df3 (you can see how the smooth scaling works). This isosurface was
created by using function{0.06 - df3_func(x,y,z)}, the 0.06 part can
then be tuned to make the surface 'grow'.
Now I wonder if it's worth doubling the integer size in the df3 to
remove some of the grain.
Post a reply to this message
Attachments:
Download 'mandelbulb_df3.jpg' (79 KB)
Preview of image 'mandelbulb_df3.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()