 |
|
|
|
|
|
| |
| |
|
|
|
|
| |
| |
|
|
I've been digging down to the foundations of computing normals, and I was
re-reading the following threads with fresh eyes.
https://news.povray.org/povray.binaries.images/thread/%3C609265e2%40news.povray.org%3E/?mtop=434022
http://news.povray.org/povray.binaries.images/thread/%3C5ff4b8da%241%40news.povray.org%3E/
https://iquilezles.org/articles/normalsSDF/
(Original pouet.net link: https://www.pouet.net/topic.php?which=5604 )
This thread recently got updated due to my inquiries, with no explanations, thus
the pyramid vectors straight from POV-Ray's normals.cpp
https://rodolphe-vaillant.fr/entry/87/normal-to-an-implicit-surface
I was also trying to re-code an old scene where I was initially trying to
replicate source-code methods in SDL, and I believe I was trying to do what
Cousin Ricky was doing - which is trying to use a scalar value to create a
"normal".
A surface normal is, by definition, a vector perpendicular to the surface at
that point. It's a vector, not a scalar, so using the scalar result from an
SDL function as a normal really doesn't make any sense.
I believe one would need to use a spline function, a pigment function, or some
other vector-valued function to properly use a function {} in a normal statement
to get meaningful if not proper results.
Perhaps what Richard is seeing is the result of vector promotion or some other
under-the-hood modification of the scalar function, and that' why the raytraced
result is wrong.
I myself am currently trying to unravel the requirements and limitations of
trying to create normals in sdf using the pyramid vector method.
All I can say is that there is no inherent bias introduced by the pyramid vector
method, since everything cancels out to give straightforward central differences
in any orientation.
- BE
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 2025-11-26 10:53 (-4), Bald Eagle wrote:
>
> I was also trying to re-code an old scene where I was initially trying to
> replicate source-code methods in SDL, and I believe I was trying to do what
> Cousin Ricky was doing - which is trying to use a scalar value to create a
> "normal".
>
> A surface normal is, by definition, a vector perpendicular to the surface at
> that point. It's a vector, not a scalar, so using the scalar result from an
> SDL function as a normal really doesn't make any sense.
So far as I understand, the scalar is an offset from the surface, and as
such, a vector perpendicular to the unperturbed surface is implied.
POV-Ray then computes a normal vector by comparing adjacent
perturbations, "adjacent" being defined by the 'accuracy' attribute.
I haven't examined the source code, so I could be wrong, but I would
expect "adjacent" samples to be free from bias, at least from opposite
directions.
> I believe one would need to use a spline function, a pigment function, or some
> other vector-valued function to properly use a function {} in a normal statement
> to get meaningful if not proper results.
This actually sounds like an excellent way to *introduce* directional
bias if you're not careful with the function. ISTR some of POV-Ray's
built-in normals already have that problem.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Cousin Ricky <ric### [at] yahoo com> wrote:
> So far as I understand, the scalar is an offset from the surface, and as
> such, a vector perpendicular to the unperturbed surface is implied.
I mean, that sounds great.
But as far as I am presently aware, POV-Ray enters the Perturb_Normal() function
in normal.cpp with no geometric information other than the "EPoint".
So in what direction do we offset from that point? The normal?
I believe that the whole reason for using the pyramid vectors is to compute the
normal in the first place so that it can then be perturbed by a vector-valued
function of amplitude bump_size or scale <x, y, z>.
I could very well be missing some key point, which is why I've been digging into
this when I have the time / remember to.
> POV-Ray then computes a normal vector by comparing adjacent
> perturbations, "adjacent" being defined by the 'accuracy' attribute.
It uses the pyramid vectors to define the sampling points offset from the EPoint
by a value "Delta" which Nathan Kopp hard-codes to 0.02.
> I haven't examined the source code, so I could be wrong, but I would
> expect "adjacent" samples to be free from bias, at least from opposite
> directions.
Yes, it's taken me some time, but I believe that the tetrahedral arrangement of
the sample points ensures exactly that, no matter the orientation.
> > I believe one would need to use a spline function, a pigment function, or some
> > other vector-valued function to properly use a function {} in a normal statement
> > to get meaningful if not proper results.
>
> This actually sounds like an excellent way to *introduce* directional
> bias if you're not careful with the function. ISTR some of POV-Ray's
> built-in normals already have that problem.
But directional bias is exactly how we are creating the normal pattern to begin
with. If we just multiplied all of the pyramid vectors by a scalar, they would
all cancel out. Because there's no inherent directional bias. In order to
"apply a normal" to a surface, we have to introduce some sort of _directional
bias_ in the form of a vector.
That vector comes from the normal pattern functions, and so I think that in
order to create a real and meaningful normal pattern like we think of them, it
needs to be a 3-dimensional vector. Otherwise, I think that "1" gets
transformed to <1, 1, 1>, "-1" gets transformed to <-1, -1, -1>, etc.
I may or may not get the opportunity to try this, but it would be useful to plot
expected normal scalar values as an overlay, and also render the potential
vector-promoted scalar values to see if they give the same results.
Definitely a lot to be learned here, on several fronts.
- BW
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"Bald Eagle" <cre### [at] netscapenet> wrote:
> I may or may not get the opportunity to try this, but it would be useful to plot
> expected normal scalar values as an overlay, and also render the potential
> vector-promoted scalar values to see if they give the same results.
Well I did. And it was as (unnecessarily) annoying, confusing, frustrating, and
difficult as these things always are.
I'm very interested in what the/your expected result is.
(very cool version statement - you have a lot of clever little things in your
scenes)
#version max (3.5, min (3.8, version));
global_settings { assumed_gamma 1 }
light_source { <(frame_number = 2? 1: -1), 1, -1.4> * 1000, rgb 1 }
camera
{ location -6 * z
right x
angle 30
}
#declare OriginalFunction =
function
{ max
( select (x - 1, 1, select (x - 2, 0, 1)),
select (y - 1, 1, select (y - 2, 0, 1))
)
}
#declare Pattern = function {
spline {
0, <0, 0, 0>,
1, <1, 1 ,1>
}
}
#declare VectorValues =
normal {
average
normal_map {
[function { Pattern (OriginalFunction(x, y, z)).red}]
[function { Pattern (OriginalFunction(x, y, z)).green}]
[function { Pattern (OriginalFunction(x, y, z)).blue}]
}
}
#declare Function = 1;
#switch (Function)
#case (0)
box
{ 0, 3
pigment { rgb <1, 0.5, 0.5> }
normal
{
function {OriginalFunction (x, y, z)}
accuracy 0.1
}
translate <-1.5, -1.5, 0>
}
#break
#case (1)
box
{ 0, 3
pigment { rgb <1, 0.5, 0.5> }
normal
{
VectorValues
accuracy 0.1
}
translate <-1.5, -1.5, 0>
}
#break
#end
#declare Ext = 5;
#for (Y, -Ext, Ext)
#for (X, -Ext, Ext)
text { ttf "arial.ttf", str (OriginalFunction (X, Y, 0), 0, 0), 0.02, 0.0
translate <-0.25, -0.25, 0> scale 0.5 translate <X, Y, -0.01> pigment {rgb
z*0.5} no_shadow}
#end
#end
Post a reply to this message
Attachments:
Download 'cousinricky_normals.png' (19 KB)
Preview of image 'cousinricky_normals.png'
|
|
| |
| |
|
|
|
|
| |
|
|
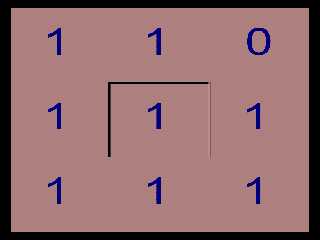
