Wasn't it Orchid XP v2 who wrote:
>Also of interest: slice the isosurface and stick a matching 2D plot on
>the cross-section! (I will do this later if I figure out pigment
>functions...)

Here are cross sections through the three axes. I used 12 iterations here
(pigment functions are a lot faster than 3d isosurfaces).

Here's the source code for the Z axis slice:-

// Just useful.
#declare ReMul = function (Xr, Xi, Yr, Yi) {Xr * Yr - Xi * Yi};
#declare ImMul = function (Xr, Xi, Yr, Yi) {Xr * Yi + Xi * Yr};

#declare Re2 = function (Zr, Zi) {  Zr*Zr - Zi*Zi};
#declare Im2 = function (Zr, Zi) {2*Zr*Zi};

#declare Re3 = function (Zr, Zi) {  Zr*Zr*Zr - 3*Zr*Zi*Zi};
#declare Im3 = function (Zr, Zi) {3*Zr*Zr*Zi -   Zi*Zi*Zi};

// Change if you like...
#declare End = function (Zr, Zi) {Zr*Zr + Zi*Zi};

// Build recursive definition...
#declare Fn = array[21];

#declare Fn[0] = function (Zr, Zi, Tr, Ti, Br, Bi) {End(Zr, Zi)};

#declare lp=1;
#while (lp<21)
   #declare Fn[lp] = function (Zr, Zi, Tr, Ti, Br, Bi)
   {
     Fn[lp-1]
     (
       Re3(Zr, Zi) - ReMul(Zr, Zi, Tr, Ti) + Br,
       Im3(Zr, Zi) - ImMul(Zr, Zi, Tr, Ti) + Bi,
       Tr, Ti, Br, Bi
     )
   };

   #declare lp = lp + 1;
#end
#undef lp

// Change this at will... (Must be < 20 tho.)
#declare Iterations = 12;

// Don't touch...
#declare InitP = function (Ar, Ai, Br, Bi) {Fn[Iterations](+Ar, +Ai,
3*Re2(Ar, Ai), 3*Im2(Ar, Ai), Br, Bi)};
#declare InitM = function (Ar, Ai, Br, Bi) {Fn[Iterations](-Ar, -Ai,
3*Re2(Ar, Ai), 3*Im2(Ar, Ai), Br, Bi)};

// Now draw something!!
camera
{
   location <0, 0, -4.5>
   look_at <0, 0, 0>
}

plane {z,0
  pigment {
    function {min(InitP(z, 0, x, y) - 4, 10)}
    colour_map {
      [0    rgb <0,0,0>]
      [0.0001 rgb <0,0,1>]
      [0.33 rgb <1,1,0>]
      [0.67 rgb <1,0,0>]
      [1.0  rgb <0,0,1>]
    }
  }
  finish {ambient 1}
  rotate z*90
  scale 2
}

Post a reply to this message

Attachments:
Download '2DMandelY.jpg' (28 KB) Download '2DMandelX.jpg' (37 KB) Download '2DMandel.jpg' (42 KB)

Preview of image '2DMandelY.jpg'

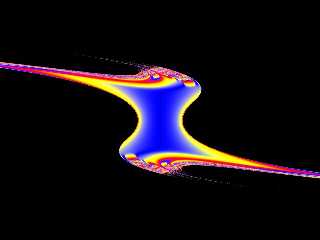
Preview of image '2DMandelX.jpg'

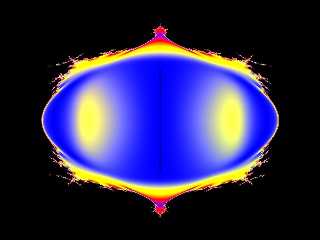
Preview of image '2DMandel.jpg'
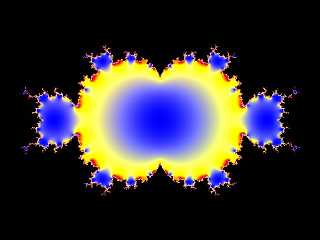