I just had another idea:

If you take a new function for your y-coordinate (which
varies linearly with u at the moment) you can have a smooth
tip. Imagine that you wander along your y-axis as u increases
from -1 to 0.4 eventually. If you start slowly, get more pace
in the middle and slow down near the end you get a smooth tip.
(I made a graph to show the y-function dependent on u).
The cubic u^2*(3-2*u) is ideal for this purpose because it
has zero-slope at u=0 and u=1. The only problem is that our
u varies from [-1, 0.4] instead of [0, 1], so we have to make
a small transformation to get our u in the range [0, 1]. We
just substitute u with (u+1)/1.4 and get the u-range right.
The last step is the scaling in y-direction, because
u^2*(3-2*u) returns values in the range [0, 1]. In summary:

   u^2*(3-2*u)                      // set (u+1)/1.4 for u
-> ((u+1)/1.4)^2*(3-(u+1)/1.4) // *1.4 // -1
-> 1.4*((u+1)/1.4)^2*(3-(u+1)/1.4)-1

The Source looks like this:

// Almost a lathe

#version 3.5;

camera { location  <3, 3, -5> look_at <0, 0, 0> angle 25}

sky_sphere { pigment {
    function{abs(y)}
    color_map { [0.0 color blue 0.6] [1.0 color rgb 1] }
  }
}

light_source {<100,200,-500> colour rgb 1}

// The open 1D spline (lathe)
#declare S = function {
   spline {
    natural_spline
    -1.0, < 0.0, 0, 0.0>,
    -0.8, < 0.4, 0, 0.5>,
    -0.5, < 0.2, 0, 0.2>,
    -0.2, < 0.2, 0, 0.2>,
     0.3, < 0.8, 0, 0.4>,
     0.4, < 0.0, 0, 0.0>,
   }
 }

#declare Fx = function(x,y) {(S(u).x * sin(v)/2)}
#declare Fy = function(x,y)
{1.4*(5/7*(u+1))*(5/7*(u+1))*(3-2*(5/7*(u+1)))-1}
#declare Fz = function(x,y) {(S(u).z * cos(v)/2)}
#declare Umin =  -1;
#declare Umax =  0.4;
#declare Vmin =  -pi;
#declare Vmax =  1.001*pi;

parametric {
  function {Fx(u,v)}
  function {Fy(u,v)}
  function {Fz(u,v)}
      <Umin,Vmin>,<Umax,Vmax>
  contained_by{box{-1,1}}
  precompute 18, x,y,z
  pigment {rgb 0.9}
  finish {phong 0.5 phong_size 10 ambient 0.2}
}

Post a reply to this message

Attachments:
Download 'u-coordinate.png' (8 KB) Download 'almost_lathe.JPG' (7 KB)

Preview of image 'u-coordinate.png'

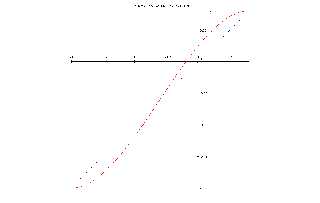
Preview of image 'almost_lathe.JPG'