|
 |
Dirk \"DIRKO\" Legler wrote:
> "Anthony D. Baye" <ban### [at] Rapidnet com> schrieb im Newsbeitrag
> news:3E4E7DB5.61F82FE8@Rapidnet.com...
> > Looking really good, however, the bowl looks like it was molded around the
> > base. Unless this is the way you wanted it, you can find the radius of
> the
> > sphere at a given point with the following equation:
>
> Sorry, but wat is "molded"? Couldn't find a translation in my dictionary..
The bowl looks as if it were formed around the central ring of the base. The
torus and spheres pass through the glass.
>
> >
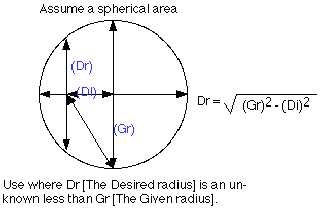
> > sqrt(pow(gr,2) - pow(dr,2)) <<-- in graphic form below.
> >
> > where <b>gr</b> is the given radius of the sphere you started with, and
> > <b>dr</b> is the desired radius. This will render the distance of that
> > radius from the center of the sphere. I use a graphing calculator for
> this,
> > but a really good scientific one will do.
>
> I wish I could afford babylon.com translator ;) Isn't it the desired radius
> that is to calculate with that equation? Or what is it for?
I inverted the parameters for desired radius and distance, so that the product
is the desired radius rather than the distance from center.
>
>
> *confused* DIRKO com> schrieb im Newsbeitrag
> news:3E4E7DB5.61F82FE8@Rapidnet.com...
> > Looking really good, however, the bowl looks like it was molded around the
> > base. Unless this is the way you wanted it, you can find the radius of
> the
> > sphere at a given point with the following equation:
>
> Sorry, but wat is "molded"? Couldn't find a translation in my dictionary..
The bowl looks as if it were formed around the central ring of the base. The
torus and spheres pass through the glass.
>
> >
> > sqrt(pow(gr,2) - pow(dr,2)) <<-- in graphic form below.
> >
> > where <b>gr</b> is the given radius of the sphere you started with, and
> > <b>dr</b> is the desired radius. This will render the distance of that
> > radius from the center of the sphere. I use a graphing calculator for
> this,
> > but a really good scientific one will do.
>
> I wish I could afford babylon.com translator ;) Isn't it the desired radius
> that is to calculate with that equation? Or what is it for?
I inverted the parameters for desired radius and distance, so that the product
is the desired radius rather than the distance from center.
>
>
> *confused* DIRKO
Post a reply to this message
Attachments:
Download 'equation.gif' (4 KB)
Preview of image 'equation.gif'
|
 |




![]()