For once in my life it looks like I properly interpreted something in 
Wikipedia and actually wrote the code to implement the psuedo-code on 
their page.

Not only that, but based on what the psuedocode was saying, I properly 
surmised how to interpolate the resulting spline functions for each 
interval.

Well, of course a spline is easy. Right?

I just wish I knew a bit more of the underlying theory of how the 
coefficients were calculated.

The article speaks of derivatives, so calculus must be involved. I'm 
gathering that the formulae in the algorithm were probably found by 
applying calculus to a 3rd order polynomial.

http://en.wikipedia.org/wiki/Cubic_spline


-- 
~Mike

Post a reply to this message

Mike Raiford wrote:

> The article speaks of derivatives, so calculus must be involved. I'm 
> gathering that the formulae in the algorithm were probably found by 
> applying calculus to a 3rd order polynomial.
> 
> http://en.wikipedia.org/wiki/Cubic_spline

Or they were derived by calculating which coefficients will yield 
continuity in the first derivative.  And maybe the second.

I am presently note-scribbling for a scene-building feature for my 
modeler, and I want something that is simple and C2 continuous when the 
user specifies continuity at a point.  I've decided to use the limit 
curves of a subdivided border (end points stay still, new mid points are 
the average of the start and end of the edge, and new interior points 
are calculated on a 1-6-1 mask).  The result is a cubic spline with C0, 
C1, and C2 continuity.  It does not necessarily pass through the control 
points, but I have a work-around for that.

C2 continuity is important in animation; if the two spline ends meet in 
the middle of a curve, and the object moving along the curve is tilted 
to show its acceleration, then any discontinuity at the join will result 
in the sudden change in the tilt of the object.  This is usually undesired.

Regards,
John

Post a reply to this message

On 24-2-2009 17:11, Mike Raiford wrote:
> For once in my life it looks like I properly interpreted something in 
> Wikipedia and actually wrote the code to implement the psuedo-code on 
> their page.
> 
> Not only that, but based on what the psuedocode was saying, I properly 
> surmised how to interpolate the resulting spline functions for each 
> interval.
> 
> Well, of course a spline is easy. Right?
> 
> I just wish I knew a bit more of the underlying theory of how the 
> coefficients were calculated.
> 
> The article speaks of derivatives, so calculus must be involved. I'm 
> gathering that the formulae in the algorithm were probably found by 
> applying calculus to a 3rd order polynomial.
> 
> http://en.wikipedia.org/wiki/Cubic_spline
> 
> 

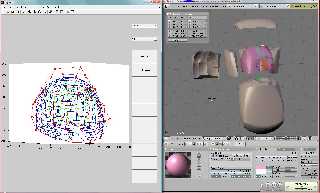
This is what my screen looks ATM. On the left my dedicated bezier volume 
editor and in blender a torso of a patient that is subdivided in 
deformed cubes. Don't ask.
I prefer Bezier because it gives easy control and it is easy to switch 
between control points and actual points on the curve. So when I need to 
subdivide a line (or volume) I compute the points where the new line 
must go through and convert that back to control points. This gives 
absolute smooth transitions between the parts. Around the heart and lung 
volumes there are discontinuities that I deliberately introduced, but 
you can not see the seams in e.g. the front of the lower body, the lower 
part is actually 5 by 4 by 2 blocks of rubber.

Post a reply to this message

Attachments:
Download 'knipsel.jpg' (263 KB)

Preview of image 'knipsel.jpg'

Mike Raiford wrote:
> Not only that, but based on what the psuedocode was saying, I properly 
> surmised how to interpolate the resulting spline functions for each 
> interval.

Nice! Sounds very smooth.

Post a reply to this message

On 2/24/2009 1:31 PM, Kevin Wampler wrote:
> Mike Raiford wrote:
>> Not only that, but based on what the psuedocode was saying, I properly
>> surmised how to interpolate the resulting spline functions for each
>> interval.
>
> Nice! Sounds very smooth.

Groan!

-- 
...Chambers
www.pacificwebguy.com

Post a reply to this message

>> Nice! Sounds very smooth.
> 
> Groan!

That Curly Phi. He's one smooth operator. ;-)

Post a reply to this message

Mike Raiford wrote:

> Well, of course a spline is easy. Right?

Heh. Not so much... ;-)

> I just wish I knew a bit more of the underlying theory of how the 
> coefficients were calculated.
> 
> The article speaks of derivatives, so calculus must be involved. I'm 
> gathering that the formulae in the algorithm were probably found by 
> applying calculus to a 3rd order polynomial.

Suppose you want a line that passes through points A and B. That is, you 
want a function f(x) such that

   f(0) = A
   f(1) = B

That's quite easy to arrange:

   f(x) = A(1-x) + Bx

This gives us a straight line between any two points. Notice that we can 
rearrange it as:

   f(x) = A(1-x) + Bx = A - Ax + Bx = (B-A)x + B

which is your usual "standard form" for a linear equation.

Now, suppose we want a curve going through *three* points, A, B and C?

   f(0.0) = A
   f(0.5) = B
   f(1.0) = C

How do we do that? Well, you can make a function

   g(0.0) = A
   g(0.5) = B

which gives us g(x) = A(1-2x) + B(2x), and another function

   h(0.5) = B
   h(1.0) = C

which gives h(x) = B(1-2(x-0.5)) + C(2(x-0.5)). If you sort out all the 
coefficients, those are both linear, and you can "blend" between them 
like this:

   f(x) = (1-x) g(x) + x h(x)

When you sort out all the algebra, you end up with a quadratic curve 
passing through all three points, as required. I've found from 
experience that this spline isn't very easy to control though!

Part of the reason for that is that if B is higher than A or C, B isn't 
necessarily the highest point on the curve. That could be to either side 
of B.

The more sophisticated splines are defined by stipulating specific 
properties the curve must have. As you have noticed, this has to do with 
calculus. In particular, the derivative of a 1D function is the *slope* 
of the graph at that point. And the second derivative is the *curvature* 
of the graph at that point. Obviously slope and curvature are useful 
things to want to control.

For example, take my defective quadratic spline above. I said that B 
isn't necessarily the highest point. In fact, if you draw a line AB and 
a line BC, you'll discover that the slope of the function doesn't match 
either of these lines at any point.

(I should perhaps point out that it's impossible for a quadratic curve 
to fit any better than this. Any three points in space uniquely define a 
single quadratic curve. For a more controllable curve, you'd need a 
higher-order polynomial.)

More sophisticated splines say "I want the slope of the graph to match 
the line AB at the start". Since "slope" is actually "first derivative", 
you end up using calculus. So you end up with something like

   f(0.0) = A
   f(0.5) = B
   f(1.0) = C
   f'(0.0) = B-A
   f'(1.0) = C-B

How you can from this system of constraints to a working function is 
just slightly beyond by level of skill. But you see where the calculus 
comes in...

Post a reply to this message