 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Any chance of this being possible
TIA
Pabs
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Yes.
Pabs wrote:
>
> Any chance of this being possible
>
> TIA
>
> Pabs
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Mr. Art" wrote:
> Yes.
How Mr Art.
Pabs
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
This short bit of code shows how to use a
planetary image as a displacement map on a sphere.
I had set it up as a macro to work with different
planet displacement maps, planet pigment maps, planet sizes,
and percentage displacements.
I know that this is displacement mapping only on a
sphere, but the same concept should work on other shapes.
I hope that this helps.
#macro PlanetMac(Pic1,Pic2,Rad,Prec)
#local Pic= function{pigment {image_map {png Pic1 interpolate 2
map_type 1}}}
#local R0=Rad;
#local FUNC1=function {"sphere",<R0>}
isosurface
{
function{FUNC1(x,y,z)-(Pic(x,y,z)*R0*Prec)}
contained_by {sphere {0,R0*(1+Prec)}}
method 2 max_gradient 10
pigment {image_map{png Pic2 interpolate 2 map_type 1}}
finish { blinn 1 facets .2 reflection 1 reflect_metallic
conserve_energy}
interior{ior 20}
}
#end
Pabs wrote:
>
> "Mr. Art" wrote:
>
> > Yes.
>
> How Mr Art.
>
> Pabs
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Mr. Art" wrote:
> This short bit of code shows how to use a
> planetary image as a displacement map on a sphere.
> I know that this is displacement mapping only on a
> sphere, but the same concept should work on other shapes.
> I hope that this helps.
I was thinking more along the lines of a patch which used isosurfaces to
implement displacement mapping
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Mark Wagner
Subject: Re: Displacement mapping using isosurfaces
Date: 12 Apr 2000 01:09:58
Message: <38f40526@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Pabs wrote in message <38F3D600.A087CAF2@hotmail.com>...
>"Mr. Art" wrote:
>
>> This short bit of code shows how to use a
>> planetary image as a displacement map on a sphere.
>> I know that this is displacement mapping only on a
>> sphere, but the same concept should work on other shapes.
>> I hope that this helps.
>
>I was thinking more along the lines of a patch which used isosurfaces to
>implement displacement mapping
How about the following code:
#declare AnObject = union{
sphere{<0,0,0>,1}
torus{1.3,0.5}
}
#declare AnObjectFunc = pigment{
object{
AnObject
}
color rgb 0, color rgb 1
}
isosurface{
function{AnObjectFunc+noise3d(x,y,z)}
contained_by{box{min_extent(AnObject),max_extent(AnObject)}
method 2
max_gradient 100
pigment{rgb 1}
}
I can't guarentee that this will work on the first try, but it will displace
the surface of any object using the noise3d function. To use a different
object, just replace AnObject with the object you want.
Mark
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
The syntax is all wrong for AnObjectFunc.
Mark Wagner wrote:
> How about the following code:
>
> #declare AnObject = union{sphere{<0,0,0>,1}torus{1.3,0.5}}
>
> #declare AnObjectFunc = pigment{object{AnObject} color rgb 0, color rgb 1}
>
> isosurface{
> function{AnObjectFunc+noise3d(x,y,z)}
> contained_by{box{min_extent(AnObject),max_extent(AnObject)}
> method 2
> max_gradient 100
> pigment{rgb 1}
> }
>
> I can't guarentee that this will work on the first try, but it will displace
> the surface of any object using the noise3d function. To use a different
> object, just replace AnObject with the object you want.
>
> Mark
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> #declare AnObjectFunc = pigment{
> object{
> AnObject
> }
> color rgb 0, color rgb 1
> }
Are you sure this works - I don't think it will unless you are thinking about
the proximity pigment func
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
In article <38f40526@news.povray.org>, "Mark Wagner"
<mar### [at] gte net> wrote:
> I can't guarentee that this will work on the first try, but it will
> displace
> the surface of any object using the noise3d function. To use a different
> object, just replace AnObject with the object you want.
I think you mean:
#declare AnObject = union {
sphere {<0,0,0>, 1}
torus {1.3, 0.5}
}
#declare AnObjectFunc =
function {
pigment {
object {AnObject color rgb 0, color rgb 1}
}
}
isosurface {
function {AnObjectFunc(x,y,z)
+noise3d(x,y,z)
}
method 2
max_gradient 100
contained_by {box {min_extent(AnObject),max_extent(AnObject)}}
pigment {color rgb <1,1,1>}
}
And the object pattern turns out to not be very good for
isosurfaces...it has two values separated by a sharp boundary, sort of
an infinite amount of slope. A boundary can appear anywhere, so the
isosurface algorithm has trouble finding them. And I don't think you
could displace the surfaces from within the function... I have a pattern
blurring feature I have been thinking of which might reduce this
problem, but I am not sure...
The proximity pattern might be helpful for this, but it is slow. You
might want to make a script that uses eval_pattern() to write the
results of proximity to a 3D density file, and use that in the
isosurface.
If your object is a blob, the blob pattern is useful. I have used it
before with very good results.
Also, don't forget that when the function goes through a pigment, you
can use warps like turbulence, black holes, etc to displace it. And with
function patterns and pigment functions, you can put any function
through a pigment. :-)
--
Christopher James Huff - Personal e-mail: chr### [at] yahoo net> wrote:
> I can't guarentee that this will work on the first try, but it will
> displace
> the surface of any object using the noise3d function. To use a different
> object, just replace AnObject with the object you want.
I think you mean:
#declare AnObject = union {
sphere {<0,0,0>, 1}
torus {1.3, 0.5}
}
#declare AnObjectFunc =
function {
pigment {
object {AnObject color rgb 0, color rgb 1}
}
}
isosurface {
function {AnObjectFunc(x,y,z)
+noise3d(x,y,z)
}
method 2
max_gradient 100
contained_by {box {min_extent(AnObject),max_extent(AnObject)}}
pigment {color rgb <1,1,1>}
}
And the object pattern turns out to not be very good for
isosurfaces...it has two values separated by a sharp boundary, sort of
an infinite amount of slope. A boundary can appear anywhere, so the
isosurface algorithm has trouble finding them. And I don't think you
could displace the surfaces from within the function... I have a pattern
blurring feature I have been thinking of which might reduce this
problem, but I am not sure...
The proximity pattern might be helpful for this, but it is slow. You
might want to make a script that uses eval_pattern() to write the
results of proximity to a 3D density file, and use that in the
isosurface.
If your object is a blob, the blob pattern is useful. I have used it
before with very good results.
Also, don't forget that when the function goes through a pigment, you
can use warps like turbulence, black holes, etc to displace it. And with
function patterns and pigment functions, you can put any function
through a pigment. :-)
--
Christopher James Huff - Personal e-mail: chr### [at] yahoo com
TAG(Technical Assistance Group) e-mail: chr### [at] tag com
TAG(Technical Assistance Group) e-mail: chr### [at] tag povray povray org
Personal Web page: http://chrishuff.dhs.org/
TAG Web page: http://tag.povray.org/ org
Personal Web page: http://chrishuff.dhs.org/
TAG Web page: http://tag.povray.org/
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> I was thinking more along the lines of a patch which used isosurfaces to
> implement displacement mapping
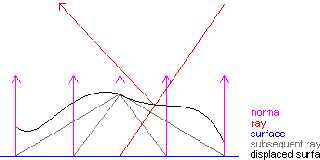
I was thinking about it & came up with the attached image
This is explained as follows
1 the ray is traced to the surface normally
2 from the point of intersection take a point d (the displacement value for
that poin in space) units along the normal for that point of intersection
this is the center of a 5*5 rectangle of points used to make a bicubic
surface (or something like that)
3 the other points are found by tracing back to the surface and then going
up the normals
4 the ray is reflected off the bicubic surface
There are a lot of problems with this but it is a start
1 It will be slow (as slow/slower as/than proximity pigment??)
2 at small angles of intersection the ray may go under the surface and miss
it
maybe the points could be got by shooting from a point along the ray instead
3 when he ray doesn't hit the original surface (but it should hit the
displaced surface) this means that edges of an object will be smooth as the
original object - maybe we could use a proximity function added to a
displacement function and convert it to an isosurface... or we could just
tesselate the whole primitive into bicubic patches...
Post a reply to this message
Attachments:
Download 'temp.gif' (4 KB)
Preview of image 'temp.gif'
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()