 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
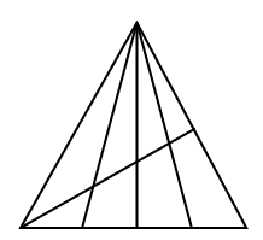
How many triangles can you find in the attached image?
Post a reply to this message
Attachments:
Download 'triangles.png' (3 KB)
Preview of image 'triangles.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Warp wrote:
> How many triangles can you find in the attached image?
None, I just see many small squares of varying shades of gray :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On Mon, 14 Dec 2009 18:26:00 -0500, Warp wrote:
> How many triangles can you find in the attached image?
I count 21.
Jim
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Jim Henderson wrote:
> On Mon, 14 Dec 2009 18:26:00 -0500, Warp wrote:
>
>> How many triangles can you find in the attached image?
>
> I count 21.
I've gone 'til 26.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Warp wrote:
> How many triangles can you find in the attached image?
Here I thought I was going to come up with a whole clever answer that didn't
need counting at all, and the numbers came out as 120. Whoops, that didn't
work.
--
Darren New, San Diego CA, USA (PST)
Human nature dictates that toothpaste tubes spend
much longer being almost empty than almost full.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
>> I count 21.
>
> I've gone 'til 26.
Heh, I got 24.
- Slime
[ http://www.slimeland.com/ ]
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Warp wrote:
> How many triangles can you find in the attached image?
>
>
Is it that time of year again? ;)
--
Best Regards,
Stephen
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 15-12-2009 1:05, nemesis wrote:
> Jim Henderson wrote:
>> On Mon, 14 Dec 2009 18:26:00 -0500, Warp wrote:
>>
>>> How many triangles can you find in the attached image?
>>
>> I count 21.
>
> I've gone 'til 26.
Wow, which ones did I miss?
Counting all that include the top and the lower line:
4 of about a quarter surface
3 of half
2 of 3/4
1 whole
That is 10
Another 10 when we don't use the lower line but the diagonal from left
bottom to right middle
The triangle that uses that diagonal and the two bottom line
and finally (?) the left most small part of that triangle
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Warp wrote:
> How many triangles can you find in the attached image?
It's the gift that keeps on giving... ;-)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> How many triangles can you find in the attached image?
I make it 24.
I thought about it like this.
There are 8 enclosed areas in the diagram, 4 at the top and 4 at the bottom.
For each triangle, each of those segments is either inside or outside the
triangle.
Consider just the top 4 segments, "0" means outside the triangle and "1"
means inside the triangle. Some combinations obviously do not form a
triangle, eg "1001" (the far left and far right segment are "inside").
The combinations that are possible to make triangles:
0000
0001
0010
0100
1000
0011
0110
1100
0111
1110
1111
For all of those apart from the "0000", there are precisely two possible
states of the bottom row of 4 segments that make valid triangles. For
"0000" there are 4 possible combinations on the bottom row that make valid
triangles. 10 x 2 + 4 = 24
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()