|
 |
Hi,
Francois LE COAT writes:
> Here is a part of Mandelbrot fractal set in 3D with my software:
>
>
> In Eureka 2.12 the function is julia(x-0.1562+i*(y+1.0323),0)
> of distances algorithm. The function julia(z,z') corresponds to
> the Mandelbrot set when z varies, and Julia when z' varies.
>
> Here is a part of Julia fractal subset in 3D with my software:
>
>
> In Eureka 2.12 the function is julia(-0.82+i*0.18,y*exp(i*x))
> plotted in [-PI/2,PI/2][0,PI/2] The 3D is obtained with the
> approximation of distances algorithm. The function julia(z,z')
> corresponds to the Mandelbrot set when z varies, and Julia when
> z' varies.
>
> The surfaces were exported from Eureka 2.12 in 3D ".TRI" format and
> transformed into a POV-Ray script with `tri2pov.ttp`. The same move
> around the surface is performed, with rotations of one degree. This
> is an illustration of the export possibilities of Eureka 2.12 =)
>
> I wish you will appreciate...
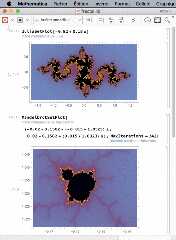
Here is corresponding Julia and Mandelbrot fractal sets with
Mathematica software, in the attached "fractal.gif" picture.
The Mandelbrot set is the same, except the colormap. But for
the Julia subset, I draw julia(-0.82+i*0.18,y*exp(i*x)) with
my software, and Mathematica draws julia(-0.82+i*0.18,x+i*y).
I don't know if there is this kind of transform in Mathematica?
Maybe someone of you all, can help?...
Merry Christmas.
Best regards,
--
Author of Eureka 2.12 (2D Graph Describer, 3D Modeller)
http://eureka.atari.org/
Post a reply to this message
Attachments:
Download 'fractal.gif' (100 KB)
Preview of image 'fractal.gif'
|
 |




![]()