On 29/03/2025 21:16, kurtz le pirate wrote:
> Yep, chatgpt is universally incomprehensible.
> 

)))
I had the same opinion, until start to use it and get results
much faster than with StackOverflow.
--
YB

Post a reply to this message

yesbird <sya### [at] gmailcom> wrote:

> I found this interesting resource: https://www.mathcurve.com/
> and want to share it with you.
> --
> YB

Here is one more site to brush up your French:

https://www.aesculier.fr/

Droj

Post a reply to this message

On 01/04/2025 19:09, Droj wrote:
> Here is one more site to brush up your French:
> 
> https://www.aesculier.fr/
> 
> Droj
> 

Thanks, I guess it's time to start learning the language of Descartes...

This part is the most interesting and very close to what I am doing now:
https://www.aesculier.fr/fichiersPovray/sextiques/sextiques.html
but unfortunately there are no parametric forms.

Btw, here is a good set of knots (English):
http://www.mi.sanu.ac.rs/vismath/taylorapril2011/Taylor.pdf
--
YB

Post a reply to this message

yesbird wrote:

> This part is the most interesting and very close to what I am doing now:
> https://www.aesculier.fr/fichiersPovray/sextiques/sextiques.html
> but unfortunately there are no parametric forms.


Very nice.  :)
I think most everyone at some point discovers these beautiful surfaces and just
_needs_ to do ... something with them.
I very much like that the circles and lines have been included in the renders.
And the regular solids!  :D

Why do you need a parametric?  Are you trying to create a mesh to decrease
render time?

> Btw, here is a good set of knots (English):
> http://www.mi.sanu.ac.rs/vismath/taylorapril2011/Taylor.pdf
> --
> YB

(will check this out later)

- BW

Post a reply to this message

On 02/04/2025 13:34, Bald Eagle wrote:
> I think most everyone at some point discovers these beautiful surfaces and just
> _needs_ to do ... something with them.

Exactly, and in my case it was at the age of eight, when I opened the
math textbook of my uncle. I was enchanted by the beauty and elegance of
curves and surfaces and later I was graduated with a Bachelor of Science
in computer graphics.

> Why do you need a parametric?  Are you trying to create a mesh to decrease
> render time?

Yes, my latest project - online editor for math surfaces and curves
assumes equations in parametric forms. MathView now in stable beta stage
and ready to be filled with a content, I am already have a large list
of candidates to this collection, fortunately they are free :).

The source of inspiration was:
https://virtualmathmuseum.org/

but I was confused by UI and quality, so decided to write my own with
modern tools, high quality and performance. You can try it here:
https://mathview.yesbird.online/

Although it's not completed yet, I will be glad to get any kind of
response, including suggestions, criticism and new ideas.

Btw, as proofing and reference tool I am using
https://www.wolframalpha.com/
and found it very useful, but having some oddities.
--
YB

Post a reply to this message

yesbird wrote:

> > Why do you need a parametric?  Are you trying to create a mesh to decrease
> > render time?
>
> Yes, my latest project - online editor for math surfaces and curves
> assumes equations in parametric forms. MathView now in stable beta stage
> and ready to be filled with a content, I am already have a large list
> of candidates to this collection, fortunately they are free :).

Hmmm.
Parameterizing is usually difficult - if not impossible for complex implicit
equations.
I'd try a variety of software packages / approaches:  Maple, etc.

Also just try to search and see what you can find.
Sometimes I find very recent solutions to projects/problems that I put to the
side only a year or two before.
Also post what you're trying to do on StackExchange/Overflow, etc. and see if
any of the people over there have any ideas, references, or solutions.
Track down anyone who has ever played with these things and see if they have any
ideas. (Jos Leys, Paul Nylander, Etienne Ghys, math professors, etc)

And then maybe just try some crazy stuff - just to see what happens.
Express everything in terms of complex numbers, or invert them through a unit
sphere and see what pops out the other end.
See if there's some 4th dimensional way to approach it.  <x, y, z, w>
Sometimes you can do what seems to make things more complex, but get a result
that is easier to process in that other "space".
So if you're able to do something like that, you might be able to parameterize
the transformed equation, and then transform it back.


One thing that you CAN do in order to speed things up is take advantage of the
symmetry of these surfaces and only calculate a part of it - then just transform
the result to cover the other areas.
So, for those surfaces that have a dodecahedron nested inside, that means there
are parts of it to match each of its 20 vertices.  So if you calculated only one
and "copied" the rest, that's 1/20th of the calculation needed.

- BW

Post a reply to this message

Since you have MatLab:

https://www.researchgate.net/publication/318476279_Algorithm_976_Bertini_real_Numerical_Decomposition_of_Real_Algebraic
_Curves_and_Surfaces/download?_tp=eyJjb250ZXh0Ijp7ImZpcnN0UGFnZSI6Il9kaXJlY3QiLCJwYWdlIjoiX2RpcmVjdCJ9fQ

https://www.researchgate.net/publication/4278665_Interactive_Ray_Tracing_of_Arbitrary_Implicits_with_SIMD_Interval_Arit
hmetic/download?_tp=eyJjb250ZXh0Ijp7ImZpcnN0UGFnZSI6Il9kaXJlY3QiLCJwYWdlIjoiX2RpcmVjdCJ9fQ

Bezier patches and Bernstein polynomials!  :)
https://cad-conference.net/files/CAD24/CAD24_334-338.pdf

Post a reply to this message

On 02/04/2025 22:30, Bald Eagle wrote:

>> Parameterizing is usually difficult - if not impossible for complex implicit
>> equations.
>> I'd try a variety of software packages / approaches:  Maple, etc.
>> 

Thanks for advice, as I said in my previous post, there are a lot of
'ready-to-use' solutions, for example, suggested by Wolfram Alpha,
and I am happy with them.


>> Since you have MatLab:
>> 
>>
https://www.researchgate.net/publication/318476279_Algorithm_976_Bertini_real_Numerical_Decomposition_of_Real_Algebraic
>>
_Curves_and_Surfaces/download?_tp=eyJjb250ZXh0Ijp7ImZpcnN0UGFnZSI6Il9kaXJlY3QiLCJwYWdlIjoiX2RpcmVjdCJ9fQ
>> 
>>
https://www.researchgate.net/publication/4278665_Interactive_Ray_Tracing_of_Arbitrary_Implicits_with_SIMD_Interval_Arit
>>
hmetic/download?_tp=eyJjb250ZXh0Ijp7ImZpcnN0UGFnZSI6Il9kaXJlY3QiLCJwYWdlIjoiX2RpcmVjdCJ9fQ
>> 
>> Bezier patches and Bernstein polynomials!  :)
>> https://cad-conference.net/files/CAD24/CAD24_334-338.pdf

Yes, I have, but MathView is based on WebGL, has no relation to
ray tracing, but in general this stuff is interesting.
-- 
YB

Post a reply to this message

On 03/04/2025 04:27, yesbird wrote:
> 
> Thanks for advice, as I said in my previous post, there are a lot of
> 'ready-to-use' solutions ...
>

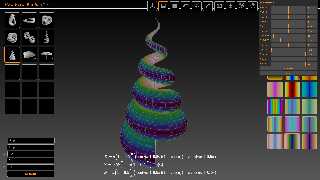
And Povray is no exception :).
In attachment is MathView vision of this canonical example:

// --------------------------------------- parametric surface -------------
#declare a = 1.0;                       // conical spiral
#declare b = 8;
#declare c = 0.2;
#declare n = 5;
parametric{
  function { a*(1-0.5*v/pi)*sin(n*v+0.5*pi)*(1-cos(u))
             + c*sin(n*v+0.5*pi) }
  function { b*0.5*v/pi + a*(1-0.5*v/pi)*sin(u) }
  function { a*(1-0.5*v/pi)*cos(n*v+0.5*pi)*(1-cos(u))
             + c*cos(n*v+0.5*pi) }
   <0,0>,<2*pi,2*pi>  // start, end of (u,v)
   contained_by {box {<-1,-1,-1>*2*pi,<1,b/3,1>*2*pi}}
   max_gradient 8  // better but slower: 10
   accuracy 0.01 // better but slower: 0.001 or smaller
   precompute 10 x,y,z
   texture{ pigment{ color rgb<1,1,1>}
            finish { phong 0.5}}
   scale 0.125
   rotate <0, 90, 0>
} // end of parametric 
----------------------------------------------------
-- 
YB

Post a reply to this message

Attachments:
Download 'test_surf.png' (464 KB)

Preview of image 'test_surf.png'

On 4/2/25 21:55, yesbird wrote:
> And Povray is no exception 🙂.
> In attachment is MathView vision of this canonical example:
> 
> // --------------------------------------- parametric surface -------------
> #declare a = 1.0;                       // conical spiral

Thanks for posting code. Below is a variation which runs quite a bit 
faster with POV-Ray for those with tiny machines like mine.

The key is the change to max_gradient. Tutorials, examples and our 
documentation have always treated / considered the parametric{} 
max_gradient in the same way as that used for the isosurface{}. However, 
they are different implementations.

The max_gradient for the parametric should often be <1.0 and it can 
sometimes be <<1.0. I "think" I suggested a default max_gradient of 0.1 
for our source code would be better, but I've not made the change as yet 
  in my yuqk fork. (A few example parametric{}s do need 1.0 or a little 
more).

Somewhere there is a forum thread and I have data and notes, but not 
finding any of it in a quick search. Anyhow, my changes for the the 
attached image:

// ------------------------------ parametric surface -------------
#declare a = 1.0;   // conical spiral
#declare b = 12;    // 8
#declare c = 0.4;   // 0.2
#declare n = 5;
#declare Para00 = parametric{
   function { a*(1-0.5*v/pi)*sin(n*v+0.5*pi)*(1-cos(u))
              + c*sin(n*v+0.5*pi) }
   function { b*0.5*v/pi + a*(1-0.5*v/pi)*sin(u) }
   function { a*(1-0.5*v/pi)*cos(n*v+0.5*pi)*(1-cos(u))
              + c*cos(n*v+0.5*pi) }
    <0,0>,<2*pi,2*pi>  // start, end of (u,v)
// contained_by {box {<-1,-1,-1>*2*pi,<1,b/3,1>*2*pi}}
    contained_by {box {<-1,-0.2,-1>*tau,<1,b/3,1>*tau}}
// max_gradient 8
    max_gradient 0.1
// accuracy 0.01
    accuracy 0.0005
    precompute 18 x,y,z
} // end of parametric

...

     union {
         object { Para00 }
         object { Para00 rotate y*+90 translate +<1,0,1>*tau}
         object { Para00 rotate y*-90 translate -<1,0,1>*tau }
         texture{
             pigment{ color rgb<1,1,1>}
             finish { emission <0.1,0,0> phong 0.5}
         }
         scale 1/b
     }

Bill P.

Post a reply to this message

Attachments:
Download 'ybspiral.png' (68 KB)

Preview of image 'ybspiral.png'