 |
|
|
|
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"And" <49341109@ntnu.edu.tw> wrote:
> Many years ago I ever do something for the same goal.
>
http://news.povray.org/povray.binaries.images/thread/%3Cweb.5264d1b954cff585cc1fd1150%40news.povray.org%3E/?ttop=4230
56&toff=750
>
> But not the same, I used the math formula, not parametric formula. And just suit
> for a small offset(a thin shell)
> Because it is just an approximation.
Outstanding! :)
This is exactly something I was trying to do and was having trouble with.
Hopefully I'll have time to look this over in detail tonight or over the
weekend.
Thanks so much for posting the link to that thread. :)
Great work!
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Wow, thanks!!
I haven't tested it yet, but I saw your note about performance. Do you
think the parametric object is slower than an isosurface? I prefer the
parametric, since all the "sketches" I've been doing in GeoGebra so far
have been with parametric formulas, and in general I find them easier to
understand. Isosurfaces always make my brain freeze.
Mike
On 7/20/2018 7:39 AM, Bald Eagle wrote:
> So, I think I started this around 10 last night and [mostly] solved it by
> midnight.
>
> I did it in parametric form, but then I couldn't get the stupid parametric to
> render, so I somehow was able to see my way to doing it in implicit form for an
> isosurface.
>
> We already know the equation for the ellipsoid
> https://en.wikipedia.org/wiki/Ellipsoid
>
> In order to derive a normal vector for each point on its surface, we need to
> know the equation of the plane tangent to the ellipsoid at those points.
>
>
http://www.math.ucla.edu/~ronmiech/Calculus_Problems/32A/chap12/section6/811d45/811_45.html
>
> and that says that the coefficients for the polynomial are the scalars of the
> normal vector.
>
> Then ya just plug that into vnormalize to get a unit normal vector and tack that
> onto the ellipsoid formula.
>
> Hit the documentation to see what the formulae for vnormalize, vlength, and vdot
> are, and you have:
>
>
> #declare R = 1;
> #declare a = 1;
> #declare b = 0.7;
> #declare c = 1;
>
> #declare F_ellipsoid = function {(pow(x,2)/pow(a,2)) + (pow(y,2)/pow(b,2))
> +(pow(z,2)/pow(c,2)) - R}
> #declare F_Normal = function {
> ((pow(x,2)/pow(a,2)) / pow(a,2)) +
> ((pow(y,2)/pow(b,2)) / pow(b,2)) +
> ((pow(z,2)/pow(c,2)) / pow(c,2)) }
>
> #declare FVdot = function {pow(((pow(x,2)/pow(a,2)) / pow(a,2)), 2) +
> pow(((pow(y,2)/pow(b,2)) / pow(b,2)), 2) + pow(((pow(z,2)/pow(c,2)) / pow(c,2)),
> 2)}
>
> #declare Normalized = function {F_Normal (x, y, z) / sqrt (FVdot (x, y, z))}
>
>
> My full scene is here.
> Perhaps someone better versed in the parametric object can determine why I can't
> get it to render the full surface, since the exact same equations are used in
> the nested loop of spheres to correctly approximate the surface.
>
> I think the only additional thing I'd do is find some way to verify the
> correctness of this solution by verifying that the distance between the offset
> curve and the ellipsoid is constant over the entire surface.
> For that, I'd likely use a trace() method for the offset and the ellipsoid, and
> then calculate the shortest Euclidean distance.
>
> Might be able to do that and rewrite my trace() based curve making script to
> plot out an approximation, and then either use a triangular grid or a series of
> rectangles to make a smooth triangle approximation of the surface like Nylander,
> Loney, TOK, and Jaap Frank.
>
>
>
> ########################################################################
>
> #version 3.8;
> global_settings {assumed_gamma 1.0}
>
> // Offset / Parallel surface of an ellipsoid.
> // Bill Walker "Bald Eagle" 7/20/2018
> // for Mike Horvath "posfan12" at
> http://news.povray.org/povray.general/thread/%3C5b513fd2%241%40news.povray.org%3E/
>
> // parametric only renders a small section - not functional yet, and SLOW
>
> #include "colors.inc"
> //#include "shapes.inc"
> //#include "shapes2.inc"
> #include "shapes3.inc"
>
> #declare Zoom = 128;
> camera {
> orthographic
> location <0, 0, -20> // position & direction of view
> look_at <0, 0, 0>
> right x*image_width/Zoom // horizontal size of view
> up y*image_height/Zoom // vertical size of view
> }
>
> camera {
> location <0, 0, -4> // position & direction of view
> look_at <0, 0, 0>
> right x*image_width/image_height // horizontal size of view
> up y // vertical size of view
> }
>
> sky_sphere {pigment {rgb <0.5, 0.5, 1>}}
> plane {y, -3 pigment {checker}}
>
> light_source {<5, 5, -30> color White}
>
>
> #declare Ellipse = torus {1, 0.01 rotate x*90 pigment {Red} scale <0.5, 1, 1> }
>
> #declare n=2;
> //object {Ellipse}
> //object {Ellipse scale <n, n, 1>}
>
>
>
>
> #declare R = 1;
> #declare a = 1;
> #declare b = 0.7;
> #declare c = 1;
>
> #declare F_ellipsoid = function {(pow(x,2)/pow(a,2)) + (pow(y,2)/pow(b,2))
> +(pow(z,2)/pow(c,2)) - R}
> #declare F_Normal = function {
> ((pow(x,2)/pow(a,2)) / pow(a,2)) +
> ((pow(y,2)/pow(b,2)) / pow(b,2)) +
> ((pow(z,2)/pow(c,2)) / pow(c,2)) }
>
> #declare FVdot = function {pow(((pow(x,2)/pow(a,2)) / pow(a,2)), 2) +
> pow(((pow(y,2)/pow(b,2)) / pow(b,2)), 2) + pow(((pow(z,2)/pow(c,2)) / pow(c,2)),
> 2)}
>
> #declare Normalized = function {F_Normal (x, y, z) / sqrt (FVdot (x, y, z))}
>
> // for dynamic adapting of the max_gradient value
> #declare Min_factor = 0.6; // between 0 and 1
> #declare MaxGradient = 4;
> #declare P0 = MaxGradient*Min_factor;
> #declare P1 = sqrt(MaxGradient/(MaxGradient*Min_factor));
> #declare P2 = 0.7; // between 0 and 1
>
> #declare Ellipsoid =
> isosurface {
> function {F_ellipsoid (x, y, z)}
> accuracy 0.001
> max_gradient 3
> //evaluate P0, P1, min (P2, 1)
> contained_by {sphere {0, R}}
> //contained_by {box {<-R, -R, -R>, <R, R, R>}}
> pigment {rgb <0, 0, 1>}
> }
>
> // for dynamic adapting of the max_gradient value
> #declare Min_factor = 0.6; // between 0 and 1
> #declare MaxGradient = 3;
> #declare P0 = MaxGradient*Min_factor;
> #declare P1 = sqrt(MaxGradient/(MaxGradient*Min_factor));
> #declare P2 = 0.7; // between 0 and 1
>
> #declare PEllipsoid =
> isosurface {
> function {F_ellipsoid (x, y, z) - Normalized (x, y, z)/5 }
> accuracy 0.001
> max_gradient 5
> //evaluate P0, P1, min (P2, 1)
> contained_by {sphere {0, R*2}}
> //contained_by {box {<-R, -R, -R>*2, <R, R, R>*2}}
> pigment {rgbt <1, 1, 0, 0.8>}
> }
>
> object {Ellipsoid}
> object {PEllipsoid} // translate x*R*2}
>
>
> #declare EllipseX = function (u, v) {a*cos(u)*sin(v)}
> #declare EllipseY = function (u, v) {b*sin(u)*sin(v)}
> #declare EllipseZ = function (v) {c*cos(v)}
>
> #declare FNormalX = function (u, v) {EllipseX (u, v) / pow(a,2)}
> #declare FNormalY = function (u, v) {EllipseY (u, v) / pow(b,2)}
> #declare FNormalZ = function (v) {EllipseZ (v) / pow(c,2)}
>
> #declare FVDot = function (u, v)
> {pow(FNormalX(u,v),2)+pow(FNormalY(u,v),2)+pow(FNormalZ(v),2)}
>
> #declare FVnormalizeX = function (u, v) {FNormalX (u, v) / sqrt (FVDot (u, v))}
> #declare FVnormalizeY = function (u, v) {FNormalY (u, v) / sqrt (FVDot (u, v))}
> #declare FVnormalizeZ = function (u, v) {FNormalZ (v) / sqrt (FVDot (u, v))}
>
> #declare Step1 = pi/18;
> #declare Step2 = pi/36;
>
> /*
> #for (V, 0, tau, Step2)
> #for (U, 0, pi, Step1)
> //#declare X = a*cos(U)*sin(V);
> #declare X = EllipseX (U, V);
> //#declare Y = b*sin(U)*sin(V);
> #declare Y = EllipseY (U, V);
> //#declare Z = c*cos(V);
> #declare Z = EllipseZ (V);
> sphere {<X, Y, Z> 0.01 pigment {Blue}} //point at <x, y, z> on the ellipsoid
>
> #declare Normal = <X/pow(a,2), Y/pow(b,2), Z/pow(c, 2)>;
> sphere {<EllipseX (U, V) + FVnormalizeX (U, V)/10, EllipseY (U, V) +
> FVnormalizeY (U, V)/10, EllipseZ (V) + FVnormalizeZ (U, V)/10> 0.01 pigment
> {Red}} // surface normal at <X, Y, Z>
> #end
> #end
> */
>
> // --------------------------------------- parametric surface --------------
> #declare Parallel = parametric {
> function {EllipseX (u, v)}
> function {EllipseY (u, v)}
> function {EllipseZ (v)}
> <0, pi>, <0, 2*pi> // start, end (u,v)
> contained_by {sphere {0, R}}
> max_gradient 50
> accuracy 0.005
> precompute 5 x,y,z
> texture {pigment{ color rgb <0, 1, 0>}}
> }
>
> //object {Parallel}
>
>
>
>
>
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Okay I have been testing your scene. I've attached an orthographic
render of an ellipsoid with equal axes (so, a sphere). You can tell in
the render that there are thicker regions at the top-left, top-right,
bottom-left, and bottom-right. So I don't think the code is working as
it should.
:(
Mike
On 7/20/2018 7:39 AM, Bald Eagle wrote:
> So, I think I started this around 10 last night and [mostly] solved it by
> midnight.
>
> I did it in parametric form, but then I couldn't get the stupid parametric to
> render, so I somehow was able to see my way to doing it in implicit form for an
> isosurface.
>
> We already know the equation for the ellipsoid
> https://en.wikipedia.org/wiki/Ellipsoid
>
> In order to derive a normal vector for each point on its surface, we need to
> know the equation of the plane tangent to the ellipsoid at those points.
>
>
http://www.math.ucla.edu/~ronmiech/Calculus_Problems/32A/chap12/section6/811d45/811_45.html
>
> and that says that the coefficients for the polynomial are the scalars of the
> normal vector.
>
> Then ya just plug that into vnormalize to get a unit normal vector and tack that
> onto the ellipsoid formula.
>
> Hit the documentation to see what the formulae for vnormalize, vlength, and vdot
> are, and you have:
>
>
> #declare R = 1;
> #declare a = 1;
> #declare b = 0.7;
> #declare c = 1;
>
> #declare F_ellipsoid = function {(pow(x,2)/pow(a,2)) + (pow(y,2)/pow(b,2))
> +(pow(z,2)/pow(c,2)) - R}
> #declare F_Normal = function {
> ((pow(x,2)/pow(a,2)) / pow(a,2)) +
> ((pow(y,2)/pow(b,2)) / pow(b,2)) +
> ((pow(z,2)/pow(c,2)) / pow(c,2)) }
>
> #declare FVdot = function {pow(((pow(x,2)/pow(a,2)) / pow(a,2)), 2) +
> pow(((pow(y,2)/pow(b,2)) / pow(b,2)), 2) + pow(((pow(z,2)/pow(c,2)) / pow(c,2)),
> 2)}
>
> #declare Normalized = function {F_Normal (x, y, z) / sqrt (FVdot (x, y, z))}
>
>
> My full scene is here.
> Perhaps someone better versed in the parametric object can determine why I can't
> get it to render the full surface, since the exact same equations are used in
> the nested loop of spheres to correctly approximate the surface.
>
> I think the only additional thing I'd do is find some way to verify the
> correctness of this solution by verifying that the distance between the offset
> curve and the ellipsoid is constant over the entire surface.
> For that, I'd likely use a trace() method for the offset and the ellipsoid, and
> then calculate the shortest Euclidean distance.
>
> Might be able to do that and rewrite my trace() based curve making script to
> plot out an approximation, and then either use a triangular grid or a series of
> rectangles to make a smooth triangle approximation of the surface like Nylander,
> Loney, TOK, and Jaap Frank.
>
>
>
> ########################################################################
>
> #version 3.8;
> global_settings {assumed_gamma 1.0}
>
> // Offset / Parallel surface of an ellipsoid.
> // Bill Walker "Bald Eagle" 7/20/2018
> // for Mike Horvath "posfan12" at
> http://news.povray.org/povray.general/thread/%3C5b513fd2%241%40news.povray.org%3E/
>
> // parametric only renders a small section - not functional yet, and SLOW
>
> #include "colors.inc"
> //#include "shapes.inc"
> //#include "shapes2.inc"
> #include "shapes3.inc"
>
> #declare Zoom = 128;
> camera {
> orthographic
> location <0, 0, -20> // position & direction of view
> look_at <0, 0, 0>
> right x*image_width/Zoom // horizontal size of view
> up y*image_height/Zoom // vertical size of view
> }
>
> camera {
> location <0, 0, -4> // position & direction of view
> look_at <0, 0, 0>
> right x*image_width/image_height // horizontal size of view
> up y // vertical size of view
> }
>
> sky_sphere {pigment {rgb <0.5, 0.5, 1>}}
> plane {y, -3 pigment {checker}}
>
> light_source {<5, 5, -30> color White}
>
>
> #declare Ellipse = torus {1, 0.01 rotate x*90 pigment {Red} scale <0.5, 1, 1> }
>
> #declare n=2;
> //object {Ellipse}
> //object {Ellipse scale <n, n, 1>}
>
>
>
>
> #declare R = 1;
> #declare a = 1;
> #declare b = 0.7;
> #declare c = 1;
>
> #declare F_ellipsoid = function {(pow(x,2)/pow(a,2)) + (pow(y,2)/pow(b,2))
> +(pow(z,2)/pow(c,2)) - R}
> #declare F_Normal = function {
> ((pow(x,2)/pow(a,2)) / pow(a,2)) +
> ((pow(y,2)/pow(b,2)) / pow(b,2)) +
> ((pow(z,2)/pow(c,2)) / pow(c,2)) }
>
> #declare FVdot = function {pow(((pow(x,2)/pow(a,2)) / pow(a,2)), 2) +
> pow(((pow(y,2)/pow(b,2)) / pow(b,2)), 2) + pow(((pow(z,2)/pow(c,2)) / pow(c,2)),
> 2)}
>
> #declare Normalized = function {F_Normal (x, y, z) / sqrt (FVdot (x, y, z))}
>
> // for dynamic adapting of the max_gradient value
> #declare Min_factor = 0.6; // between 0 and 1
> #declare MaxGradient = 4;
> #declare P0 = MaxGradient*Min_factor;
> #declare P1 = sqrt(MaxGradient/(MaxGradient*Min_factor));
> #declare P2 = 0.7; // between 0 and 1
>
> #declare Ellipsoid =
> isosurface {
> function {F_ellipsoid (x, y, z)}
> accuracy 0.001
> max_gradient 3
> //evaluate P0, P1, min (P2, 1)
> contained_by {sphere {0, R}}
> //contained_by {box {<-R, -R, -R>, <R, R, R>}}
> pigment {rgb <0, 0, 1>}
> }
>
> // for dynamic adapting of the max_gradient value
> #declare Min_factor = 0.6; // between 0 and 1
> #declare MaxGradient = 3;
> #declare P0 = MaxGradient*Min_factor;
> #declare P1 = sqrt(MaxGradient/(MaxGradient*Min_factor));
> #declare P2 = 0.7; // between 0 and 1
>
> #declare PEllipsoid =
> isosurface {
> function {F_ellipsoid (x, y, z) - Normalized (x, y, z)/5 }
> accuracy 0.001
> max_gradient 5
> //evaluate P0, P1, min (P2, 1)
> contained_by {sphere {0, R*2}}
> //contained_by {box {<-R, -R, -R>*2, <R, R, R>*2}}
> pigment {rgbt <1, 1, 0, 0.8>}
> }
>
> object {Ellipsoid}
> object {PEllipsoid} // translate x*R*2}
>
>
> #declare EllipseX = function (u, v) {a*cos(u)*sin(v)}
> #declare EllipseY = function (u, v) {b*sin(u)*sin(v)}
> #declare EllipseZ = function (v) {c*cos(v)}
>
> #declare FNormalX = function (u, v) {EllipseX (u, v) / pow(a,2)}
> #declare FNormalY = function (u, v) {EllipseY (u, v) / pow(b,2)}
> #declare FNormalZ = function (v) {EllipseZ (v) / pow(c,2)}
>
> #declare FVDot = function (u, v)
> {pow(FNormalX(u,v),2)+pow(FNormalY(u,v),2)+pow(FNormalZ(v),2)}
>
> #declare FVnormalizeX = function (u, v) {FNormalX (u, v) / sqrt (FVDot (u, v))}
> #declare FVnormalizeY = function (u, v) {FNormalY (u, v) / sqrt (FVDot (u, v))}
> #declare FVnormalizeZ = function (u, v) {FNormalZ (v) / sqrt (FVDot (u, v))}
>
> #declare Step1 = pi/18;
> #declare Step2 = pi/36;
>
> /*
> #for (V, 0, tau, Step2)
> #for (U, 0, pi, Step1)
> //#declare X = a*cos(U)*sin(V);
> #declare X = EllipseX (U, V);
> //#declare Y = b*sin(U)*sin(V);
> #declare Y = EllipseY (U, V);
> //#declare Z = c*cos(V);
> #declare Z = EllipseZ (V);
> sphere {<X, Y, Z> 0.01 pigment {Blue}} //point at <x, y, z> on the ellipsoid
>
> #declare Normal = <X/pow(a,2), Y/pow(b,2), Z/pow(c, 2)>;
> sphere {<EllipseX (U, V) + FVnormalizeX (U, V)/10, EllipseY (U, V) +
> FVnormalizeY (U, V)/10, EllipseZ (V) + FVnormalizeZ (U, V)/10> 0.01 pigment
> {Red}} // surface normal at <X, Y, Z>
> #end
> #end
> */
>
> // --------------------------------------- parametric surface --------------
> #declare Parallel = parametric {
> function {EllipseX (u, v)}
> function {EllipseY (u, v)}
> function {EllipseZ (v)}
> <0, pi>, <0, 2*pi> // start, end (u,v)
> contained_by {sphere {0, R}}
> max_gradient 50
> accuracy 0.005
> precompute 5 x,y,z
> texture {pigment{ color rgb <0, 1, 0>}}
> }
>
> //object {Parallel}
>
>
>
>
>
Post a reply to this message
Attachments:
Download 'bald_eagle_text.png' (27 KB)
Preview of image 'bald_eagle_text.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Just to be clear, the offset surface of a perfect sphere should be
another perfect sphere.
Mike
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 7/20/2018 10:02 AM, And wrote:
> Many years ago I ever do something for the same goal.
>
http://news.povray.org/povray.binaries.images/thread/%3Cweb.5264d1b954cff585cc1fd1150%40news.povray.org%3E/?ttop=423056
> &toff=750
>
> But not the same, I used the math formula, not parametric formula. And just suit
> for a small offset(a thin shell)
> Because it is just an approximation.
>
>
>
Very nice, thanks!
I did a test, but there are graphical artifacts related to max_gradient
I think. The docs say a warning should appear if max_gradient is too far
off, but I don't see such a warning.
#############################################
#version 3.8;
global_settings {assumed_gamma 1.0}
#declare Zoom = 128;
camera
{
orthographic
location -z * 128 // position & direction of view
direction +z
right x*image_width/Zoom // horizontal size of view
up y*image_height/Zoom // vertical size of view
rotate x * 15
rotate y * 45
}
/*
camera
{
location <0, 0, -4> // position & direction of view
look_at <0, 0, 0>
right x*image_width/image_height // horizontal size of view
up y // vertical size of view
rotate x * 15
rotate y * 15
}
*/
sky_sphere {pigment {rgb <0.5, 0.5, 1>}}
plane {y, -3 pigment {checker}}
light_source {<30, 30, -30> color rgb 1 parallel point_at 0}
#declare surf_thick = 0.1;
#declare f_spheroid = function(var1,var2,var3, a,b)
{var1*var1/a/a+var2*var2/a/a+var3*var3/b/b-1}
#declare f_spheroid_normalized = function(var1,var2,var3, a,b)
{f_spheroid(var1,var2,var3,
a,b)/sqrt(4*(var1*var1+var2*var2)/pow(a,4)+4*var3*var3/pow(b,4))}
//than difference these two isosurfaces
difference
{
isosurface
{
function {f_spheroid_normalized(x,y,z,1,2)-surf_thick}
// accuracy 0.001
max_gradient 4
//evaluate P0, P1, min (P2, 1)
contained_by {sphere {0, 4}}
}
isosurface
{
function {f_spheroid(x,y,z,1,2)}
// accuracy 0.001
max_gradient 4
//evaluate P0, P1, min (P2, 1)
contained_by {sphere {0, 4}}
}
plane {-y, 0}
pigment {color rgbt <1,1,1,1/4>}
}
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
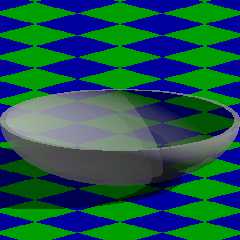
It's all working now, thanks to you all!
I've attached the latest test code and render.
Mike
Post a reply to this message
Attachments:
Download 'and_test.pov.txt' (2 KB)
Download 'and_test.png' (40 KB)
Preview of image 'and_test.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Am 21.07.2018 um 04:46 schrieb Mike Horvath:
> Wow, thanks!!
>
> I haven't tested it yet, but I saw your note about performance. Do you
> think the parametric object is slower than an isosurface? I prefer the
> parametric, since all the "sketches" I've been doing in GeoGebra so far
> have been with parametric formulas, and in general I find them easier to
> understand. Isosurfaces always make my brain freeze.
My gut feeling is that for any given task there's nothing slower than
isosurfaces. After all, isosurfaces are pretty much the pinnacle of
flexibility, so they also provide the least potential for optimization.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Mike Horvath <mik### [at] gmail com> wrote:
> It's all working now, thanks to you all!
>
> I've attached the latest test code and render.
>
That's some really nice math work and problem-solving. I played around with the
bowl thickness and object scaling in your code, just to test the 'uniform wall
thickness' idea-- which works well!
You might try scaling the final bounded_by object to more closely fit the
resulting isosurface (for the sole purpose of making the scene render a bit
faster.) Even though the initial two isosurfaces' contained_by spheres can't be
scaled (that is, *non-uniformly* scaled), the final bounded_by sphere can. For
my render, I used <2.0,0.8,0.7> in the two initial functions...
function {f_spheroid(x,y,z,2.0,0.8,0.7)}
and
function {f_spheroid_normalized(x,y,z,2.0,0.8,0.7)+surf_thick}
.... with surf_thick = 0.4, and bounded_by{sphere{0,1 scale <2.0, 0.8, 0.7>}}
This works well; I even tested the resulting (hidden) 'bounding box' shape with
min_extent/max_extent, to make sure of the close fit.
Of course. maybe a scaled BOX for the bounded_by shape could be an even closer
fit (to coincide with the differenced PLANE object in your code.)
I did notice some artifacts, in the self-shadowing area of the bowl. From
testing various things, it seems to be solely due to the isosurface 'accuracy'
value. I changed that from 0.001 to 0.000001, which appears to eliminate the
Moire patterns there. (I actually don't know how *small* a value that accuracy
can be, before it has no further effect.)
I was going to attach an image here of my tests, but I can't (using the web
interface, anyway.) I'll post it to the images section instead.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 7/24/2018 6:15 PM, Kenneth wrote:
> Mike Horvath <mik### [at] gmailcom> wrote:
>> It's all working now, thanks to you all!
>>
>> I've attached the latest test code and render.
>>
>
> That's some really nice math work and problem-solving. I played around with the
> bowl thickness and object scaling in your code, just to test the 'uniform wall
> thickness' idea-- which works well!
>
Thanks!
> You might try scaling the final bounded_by object to more closely fit the
> resulting isosurface (for the sole purpose of making the scene render a bit
> faster.) Even though the initial two isosurfaces' contained_by spheres can't be
> scaled (that is, *non-uniformly* scaled), the final bounded_by sphere can. For
> my render, I used <2.0,0.8,0.7> in the two initial functions...
> function {f_spheroid(x,y,z,2.0,0.8,0.7)}
> and
> function {f_spheroid_normalized(x,y,z,2.0,0.8,0.7)+surf_thick}
>
> .... with surf_thick = 0.4, and bounded_by{sphere{0,1 scale <2.0, 0.8, 0.7>}}
>
> This works well; I even tested the resulting (hidden) 'bounding box' shape with
> min_extent/max_extent, to make sure of the close fit.
>
> Of course. maybe a scaled BOX for the bounded_by shape could be an even closer
> fit (to coincide with the differenced PLANE object in your code.)
>
> I did notice some artifacts, in the self-shadowing area of the bowl. From
> testing various things, it seems to be solely due to the isosurface 'accuracy'
> value. I changed that from 0.001 to 0.000001, which appears to eliminate the
> Moire patterns there. (I actually don't know how *small* a value that accuracy
> can be, before it has no further effect.)
>
> I was going to attach an image here of my tests, but I can't (using the web
> interface, anyway.) I'll post it to the images section instead.
>
>
>
I'm not too worried about the artifacts, since 99% of the shape is
hidden behind another texture. Only the edges are important to me. (See
globe render in p.b.i.)
Mike
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 7/24/2018 6:36 PM, Mike Horvath wrote:
> I'm not too worried about the artifacts, since 99% of the shape is
> hidden behind another texture. Only the edges are important to me. (See
> globe render in p.b.i.)
>
>
> Mike
p.b.a rather
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
|
|
