 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hi there,
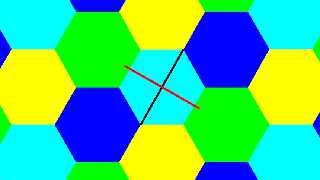
why does the hexagon pattern in Povray only supports 3 colors?
I'd like to have a hexagonal pattern with 4 or 7 colors, see attached
images.
How can I do that with current povray versions?
Is it planned for a future release to make it easier?
Greetings,
Lars R.
Post a reply to this message
Attachments:
Download 'hexagon-4colors.jpg' (26 KB)
Download 'hexagon-7colors.jpg' (29 KB)
Preview of image 'hexagon-4colors.jpg'
Preview of image 'hexagon-7colors.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 26.04.2018 um 09:15 schrieb Lars R.:
> Hi there,
>
> why does the hexagon pattern in Povray only supports 3 colors?
>
> I'd like to have a hexagonal pattern with 4 or 7 colors, see attached
> images.
And other users might want their hexagonal pattern with 11 colours, or
17, or 32. Or maybe 723.
We can't provide dedicated support for /all/ use cases our users might
come up with; we have to draw a line somewhere.
With a hexagonal pattern, 3 colours is the minimum you need to tile the
plane without having adjacent tiles of same colour, so that's the
"natural" number of colours for that tiling.
If you need a special variant of the hexagonal pattern, you can
implement it using a function pattern based on a user-defined function.
It's not easy, but it can be done. You'll need a lot of `switch()`, a
bit of trignonometry I guess, and maybe some `mod()` to achieve the
repetition.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
clipka <ano### [at] anonymous org> wrote:
> If you need a special variant of the hexagonal pattern, you can
> implement it using a function pattern based on a user-defined function.
> It's not easy,
True. I took a brief stab at this back in the Quantum Dot thread.
> but it can be done.
Yes. And such a function would be great fun to experiment with.
> You'll need a lot of `switch()`, a
> bit of trignonometry I guess, and maybe some `mod()` to achieve the
> repetition.
Perhaps if the existing POV-Ray internal function code were posted here, that
would provide a good jumping-off point? org> wrote:
> If you need a special variant of the hexagonal pattern, you can
> implement it using a function pattern based on a user-defined function.
> It's not easy,
True. I took a brief stab at this back in the Quantum Dot thread.
> but it can be done.
Yes. And such a function would be great fun to experiment with.
> You'll need a lot of `switch()`, a
> bit of trignonometry I guess, and maybe some `mod()` to achieve the
> repetition.
Perhaps if the existing POV-Ray internal function code were posted here, that
would provide a good jumping-off point?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Perhaps if the existing POV-Ray internal function code were posted here, that
> would provide a good jumping-off point?
Good idea Bill, get on that, will you?
Right.
Here ya go.
From fnintern.cpp
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int fn); // 27
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int fn); // 28
const Trap POVFPU_TrapTable[] =
{
{ f_hex_x, 1 + 3 }, // 27
{ f_hex_y, 1 + 3 }, // 28
};
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int) // 27
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(x1);
else
{
x1=cos(M_PI/3)*x1+sin(M_PI/3)*y1;
return(x1);
}
}
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int) // 28
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(y1);
else
{
y1=-sin(M_PI/3)*x1+cos(M_PI/3)*y1;
return(fabs(y1));
}
} net> wrote:
> Perhaps if the existing POV-Ray internal function code were posted here, that
> would provide a good jumping-off point?
Good idea Bill, get on that, will you?
Right.
Here ya go.
From fnintern.cpp
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int fn); // 27
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int fn); // 28
const Trap POVFPU_TrapTable[] =
{
{ f_hex_x, 1 + 3 }, // 27
{ f_hex_y, 1 + 3 }, // 28
};
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int) // 27
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(x1);
else
{
x1=cos(M_PI/3)*x1+sin(M_PI/3)*y1;
return(x1);
}
}
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int) // 28
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(y1);
else
{
y1=-sin(M_PI/3)*x1+cos(M_PI/3)*y1;
return(fabs(y1));
}
}
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
[Experiencing some problems with the website: Trying this again]
"Bald Eagle" <cre### [at] netscape net> wrote:
> Perhaps if the existing POV-Ray internal function code were posted here, that
> would provide a good jumping-off point?
Good idea Bill, get on that, will you?
Right.
Here ya go.
From fnintern.cpp
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int fn); // 27
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int fn); // 28
const Trap POVFPU_TrapTable[] =
{
{ f_hex_x, 1 + 3 }, // 27
{ f_hex_y, 1 + 3 }, // 28
};
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int) // 27
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(x1);
else
{
x1=cos(M_PI/3)*x1+sin(M_PI/3)*y1;
return(x1);
}
}
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int) // 28
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(y1);
else
{
y1=-sin(M_PI/3)*x1+cos(M_PI/3)*y1;
return(fabs(y1));
}
} net> wrote:
> Perhaps if the existing POV-Ray internal function code were posted here, that
> would provide a good jumping-off point?
Good idea Bill, get on that, will you?
Right.
Here ya go.
From fnintern.cpp
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int fn); // 27
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int fn); // 28
const Trap POVFPU_TrapTable[] =
{
{ f_hex_x, 1 + 3 }, // 27
{ f_hex_y, 1 + 3 }, // 28
};
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int) // 27
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(x1);
else
{
x1=cos(M_PI/3)*x1+sin(M_PI/3)*y1;
return(x1);
}
}
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int) // 28
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(y1);
else
{
y1=-sin(M_PI/3)*x1+cos(M_PI/3)*y1;
return(fabs(y1));
}
}
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> [Experiencing some problems with the website: Trying this again]
Apparently there was a hiccup.
I tried to play with this a bit last night, and wanted to do it using functions,
so I could wind up with a pigment {function{}}
Is there a syntax by which I can do a function of a function?
I'm looking to something along the lines of:
#declare A = function (b, d) {b+d}
#declare Q = function (A(b,d), k) {A*k}
but POV-Ray doesn't calculate the result of A to be used as a parameter of Q.
It complains that it's expecting a parameter, but found a function instead.
I'm thinking there ought to be a way to G(F(x)).
Anyone? net> wrote:
> [Experiencing some problems with the website: Trying this again]
Apparently there was a hiccup.
I tried to play with this a bit last night, and wanted to do it using functions,
so I could wind up with a pigment {function{}}
Is there a syntax by which I can do a function of a function?
I'm looking to something along the lines of:
#declare A = function (b, d) {b+d}
#declare Q = function (A(b,d), k) {A*k}
but POV-Ray doesn't calculate the result of A to be used as a parameter of Q.
It complains that it's expecting a parameter, but found a function instead.
I'm thinking there ought to be a way to G(F(x)).
Anyone?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 27.04.2018 um 14:02 schrieb Bald Eagle:
> Is there a syntax by which I can do a function of a function?
>
> I'm looking to something along the lines of:
>
> #declare A = function (b, d) {b+d}
> #declare Q = function (A(b,d), k) {A*k}
>
> but POV-Ray doesn't calculate the result of A to be used as a parameter of Q.
> It complains that it's expecting a parameter, but found a function instead.
>
> I'm thinking there ought to be a way to G(F(x)).
That depends on what you are trying to achieve.
For G(F(x)), how about
#declare F = function(x) { x+1 }
#declare G = function(y) { y*y }
#declare Foo = G(F(4711)); // ((4711)+1)^2
Or, if you want to "hide" F(x) inside G(x), how about
#declare F = function(x) { x+1 }
#declare G = function(x) { F(x)*F(x) }
#declare Foo = G(4711); // ((4711)+1)^2
As a side note to the latter case, note that F(x) will be invoked twice
per invocation of G(x); to avoid this, in such cases I tend to use a mix
of the above:
#declare F = function(x) { x^2 }
#declare G_ = function(y) { y*y }
#declare G = function(x) { G_(F(x)) }
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 26.04.2018 um 21:44 schrieb Bald Eagle:
>> Perhaps if the existing POV-Ray internal function code were posted here, that
>> would provide a good jumping-off point?
>
> Good idea Bill, get on that, will you?
> Right.
> Here ya go.
>
> From fnintern.cpp
>
> DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int fn); // 27
> DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int fn); // 28
"These are not the functions you are looking for."
To the best of my knowledge, those functions actually correspond to the
`tiling 2` pattern, not the `hexagon` pattern.
The `hexagon` pattern is implemented by `HexagonPattern::Evaluate()` in
`source/core/material/pattern.cpp` (approx. line 6510).
Note however that the function is implemented using imperative
programming, and needs to be re-formulated as a pure function in order
to implement it as an SDL function.
Also, the function returns values 0, 1 or 2 to select the texture,
whereas a function to be used in a function-based pigment needs to
return values in the rang 0..1 (e.g. 0/N, 1/N, 2/N, ..., N/N) to select
the texture from a texture map.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
clipka <ano### [at] anonymous org> wrote:
> "These are not the functions you are looking for."
Your Jedi mind tricks don't work on me, clipka.
> To the best of my knowledge, those functions actually correspond to the
> `tiling 2` pattern, not the `hexagon` pattern.
I think there may be other closely related patterns in that same file, however
the functions.inc references the f_hex_x pattern, and I came across this early
thread, which I think might be before the pavement tilings were available.
http://news.povray.org/povray.general/thread/%3Cj### [at] netplex org> wrote:
> "These are not the functions you are looking for."
Your Jedi mind tricks don't work on me, clipka.
> To the best of my knowledge, those functions actually correspond to the
> `tiling 2` pattern, not the `hexagon` pattern.
I think there may be other closely related patterns in that same file, however
the functions.inc references the f_hex_x pattern, and I came across this early
thread, which I think might be before the pavement tilings were available.
http://news.povray.org/povray.general/thread/%3Cj### [at] netplex aussie aussie org%3E/?ttop=285799&toff=320
0
> The `hexagon` pattern is implemented by `HexagonPattern::Evaluate()` in
> `source/core/material/pattern.cpp` (approx. line 6510).
Well, I'll certainly give it all a look over as time is available.
> Note however that the function is implemented using imperative
> programming, and needs to be re-formulated as a pure function in order
> to implement it as an SDL function.
Yes, I had gotten that far, and believe I _might_ be able to do it with a few
functions and select() [The code is at home, otherwise I'd post it for
early-stage critical review]
> Also, the function returns values 0, 1 or 2 to select the texture,
> whereas a function to be used in a function-based pigment needs to
> return values in the rang 0..1 (e.g. 0/N, 1/N, 2/N, ..., N/N) to select
> the texture from a texture map.
Yep, I think that's the idea. Hopefully I'll be able to figure that part out
once I get the basics worked out and can better see the overall picture of how
to construct the pattern.
However, I'm also wondering if I can't somehow come up with a pattern that would
allow the tricks over in the bricks pattern thread to be used. Or if somehow
that trick can be applied to the existing hexagon pattern[s] to eliminate the
need for writing a special function. org%3E/?ttop=285799&toff=320
0
> The `hexagon` pattern is implemented by `HexagonPattern::Evaluate()` in
> `source/core/material/pattern.cpp` (approx. line 6510).
Well, I'll certainly give it all a look over as time is available.
> Note however that the function is implemented using imperative
> programming, and needs to be re-formulated as a pure function in order
> to implement it as an SDL function.
Yes, I had gotten that far, and believe I _might_ be able to do it with a few
functions and select() [The code is at home, otherwise I'd post it for
early-stage critical review]
> Also, the function returns values 0, 1 or 2 to select the texture,
> whereas a function to be used in a function-based pigment needs to
> return values in the rang 0..1 (e.g. 0/N, 1/N, 2/N, ..., N/N) to select
> the texture from a texture map.
Yep, I think that's the idea. Hopefully I'll be able to figure that part out
once I get the basics worked out and can better see the overall picture of how
to construct the pattern.
However, I'm also wondering if I can't somehow come up with a pattern that would
allow the tricks over in the bricks pattern thread to be used. Or if somehow
that trick can be applied to the existing hexagon pattern[s] to eliminate the
need for writing a special function.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
So, IRL is busy and chaotic, but here's what I have so far in case anyone can
point out some obvious mistakes.
Obviously I will try out other variations and source code functions...
#version 3.7;
global_settings {assumed_gamma 1.0}
#include "colors.inc"
sky_sphere {pigment {rgb <1, 1, 1>*0.2}}
camera {
location <0, 0, -150> // position & direction of view
look_at <0, 0, 0>
right x*image_width/image_height // horizontal size of view
up y // vertical size of view
}
light_source {<25, 25, -150> color White}
//From fnintern.cpp
/*
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int fn); // 27
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int fn); // 28
const Trap POVFPU_TrapTable[] =
{
{ f_hex_x, 1 + 3 }, // 27
{ f_hex_y, 1 + 3 }, // 28
};
DBL f_hex_x(FPUContext *ctx, DBL *ptr, unsigned int) // 27
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(x1);
else
{
x1=cos(M_PI/3)*x1+sin(M_PI/3)*y1;
return(x1);
}
}
*/
#declare S3 = sqrt(3.0);
#declare S32 = sqrt(3.0)/2;
#declare x1 = function (x) {abs(mod(abs(x), S3)-S32)}
#declare y1 = function (y) {abs(mod(abs(y), 3)-1.5)}
#declare x2 = function (x) {S32-x1(x)}
#declare y2 = function (y) {1.5-y1(y)}
#declare X0 = 0.000001;
#declare X1 = function (x, y) {select
((x1(x)*x1(x)+y1(y)*y1(y))-(x2(x)*x2(x)+y2(y)*y2(y)), x2(x), x1(x), x1(x))}
#declare Y1 = function (x, y) {select
((x1(x)*x1(x)+y1(y)*y1(y))-(x2(x)*x2(x)+y2(y)*y2(y)), y2(y), y1(y), y1(y))}
#declare Th = function (x, y) {select (X1(x1(x), y1(y))*Y1(x1(x), y1(y)),
atan2(Y1(x1(x), y1(y)), X0), atan2(Y1(x1(x), y1(y)), X1(x1(x), y1(y))),
atan2(Y1(x1(x), y1(y)), X0))}
#declare Hexagonal = function (x, y) {select(Th(X1(x1(x), y1(y)), Y1(x1(x),
y1(y)))-(pi/6), X1(x1(x), y1(y)), cos(pi/3)*Y1(x1(x), y1(y))+sin(pi/3)*Y1(x1(x),
y1(y)))}
#declare Hex = pigment {
function {Hexagonal (x, y)}
color_map {
[0.00 rgb 0]
[1.00 rgb 1]
}
scale 10
}
box {<1,1,0.0001>*-50, <1,1,0.0001>*50 pigment {Hex} }
/*
DBL f_hex_y(FPUContext *ctx, DBL *ptr, unsigned int) // 28
{
DBL x1,y1,x2,y2, th;
x1=fabs(fmod(fabs(PARAM_X), sqrt(3.0))-sqrt(3.0)/2);
y1=fabs(fmod(fabs(PARAM_Y), 3)-1.5);
x2=sqrt(3.0)/2-x1;
y2=1.5-y1;
if ((x1*x1+y1*y1)>(x2*x2+y2*y2))
{
x1=x2;
y1=y2;
}
if ((x1==0)&&(y1==0))
PARAM_X=0.000001;
th=atan2(y1,x1);
if (th<M_PI/6)
return(y1);
else
{
y1=-sin(M_PI/3)*x1+cos(M_PI/3)*y1;
return(fabs(y1));
}
}
*/
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()