 |
|
|
|
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"jr" <cre### [at] gmail com> wrote:
> I'll reply tomorrow (Sunday), via email, on topic.
Well, before I go changing the documentation for POV-Ray, I'd like to point out
that currently I have only worked out some form of the Catmull-Rom spline that
seems to work in a predictable way.
I'm currently at the state where I'm looking at the source code in sor.cpp to
try and figure out if the 2 things match in some way.
https://github.com/POV-Ray/povray/blob/master/source/core/shape/sor.cpp
1. The source uses the x and y values of the control points separately in the
terms of the equations used to solve for the coefficients. I do not.
2. The source uses powers of the control point y values in the matrix, whereas I
do not.
3. The source performs a matrix inversion before calculating the coefficients.
No idea why, or what that does (yet).
4. Then there are other adjustments after that,
c[0] = 3.0 * A;
c[1] = 2.0 * B;
c[2] = C;
5. and then they somehow need to "solve a polynomial" - presumably to find a
root.
n = Solve_Polynomial(2, c, r, false, 0.0, stats);
6. then this n value is used as the iterator in the interpolation
while (n--)
{
if ((r[n] >= y[0]) && (r[n] <= y[1]))
{
x[n] = sqrt(r[n] * (r[n] * (r[n] * A + B) + C) + D);
}
}
Which all seems bewilderingly complex to me, but seems to jive with current
documentation.
HOW that all works is currently beyond me.
It's just a giant big black box.
Somewhere around 2000, it seemed to be beyond Warp as well.
I have some thing to do today and tomorrow, but Maybe I can spin my version
around the y-axis and compare it the actual sor object and see if they're even
close.
- BW
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
At the moment, everything is looking to more or less ok, there probably only
needs to be a minor amount of clarification and explanation to make the
documentation sufficiently user-friendly.
I added some comments to the source code for sor.cpp
and hopefully I can make a little more progress on comparing my own version
written from scratch to what's going on in source.
There are normal, chordal, and centripetal forms.
I suspect mine is the normal form, and the one in source is centripetal.
(I will need to check source against the following, which I stumbled upon)
https://splines.readthedocs.io/en/latest/euclidean/catmull-rom-properties.html
So the first thing we need to do is set up our system of equations that relates
a cubic interpolation between the START (P1) and END (P2) points of the spline
to the constraints for the data, namely that the spline has to pass _through_
the endpoints, and the tangents at the endpoints for the spline segments are
defined using the additional spline points P0 and P3.
Following along with the comments that summarize the matrix values, it will be
fairly easy to match this up with what is going on in this video:
https://www.youtube.com/watch?v=DLsqkWV6Cag
/* Use cubic interpolation. */
k[0] = P[i+1][X] * P[i+1][X]; // P1.x^2, actual spline start
k[1] = P[i+2][X] * P[i+2][X]; // P2.x^2, actual spline end
k[2] = (P[i+2][X] - P[i][X]) / (P[i+2][Y] - P[i][Y]); // df/dt at
spline start
k[3] = (P[i+3][X] - P[i+1][X]) / (P[i+3][Y] - P[i+1][Y]); // df/dt at
spline end (tangent)
k[2] *= 2.0 * P[i+1][X]; // = 2 P1.x * (P2.x - P0.x)
----------------------
(P2.y - P0.y)
k[3] *= 2.0 * P[i+2][X]; // = 2 P2.x * (P3.x - P1.x)
----------------------
(P3.y - P1.y)
w = P[i+1][Y];
Mat[0][0] = w * w * w; // P1.y^3
Mat[0][1] = w * w; // P1.y^2
Mat[0][2] = w; // P1.y
Mat[0][3] = 1.0; // 1
Mat[2][0] = 3.0 * w * w; // 3*P1.y^2
Mat[2][1] = 2.0 * w; // 2*P1.y
Mat[2][2] = 1.0; // 1
Mat[2][3] = 0.0; // 0
w = P[i+2][Y];
Mat[1][0] = w * w * w; // P2.y^3
Mat[1][1] = w * w; // P2.y^2
Mat[1][2] = w; // P2.y
Mat[1][3] = 1.0; // 1
Mat[3][0] = 3.0 * w * w; // 3*P2.y^2
Mat[3][1] = 2.0 * w; // 2*P2.y
Mat[3][2] = 1.0; // 1
Mat[3][3] = 0.0; // 0
-------------------------------------------------------------------------
One can solve a system of linear equations in a matrix using a number of
different methods.
The source uses the method of finding the matrix inverse, and then multiplying
both sides of the matrix equation by the matrix inverse.
(This is where the over-brief equation in the docs is confusing, without any
other context)
-------------------------------------------------------------------------
// Now we find the matrix inverse so that we can solve for the coefficients
/*
ax = b
(1/a)*ax = (1/a)*b
(a^-1)ax = (a^-1)b
(a^-1)*x = 1, so
x = (a^-1) b
*/
MInvers(Mat, Mat); // in math/matrix.cpp
// Once we have the matrix inverse, we take the data constraints and the matrix
inverse and
// multiply them to calculate the coefficients.
/* Calculate coefficients of cubic patch. */
// k[] is the column vector of the constraints
// and Mat[] is the *matrix_inverse* M
// so multiplying together equals the column vector of the coefficients
A = k[0] * Mat[0][0] + k[1] * Mat[0][1] + k[2] * Mat[0][2] + k[3] *
Mat[0][3];
B = k[0] * Mat[1][0] + k[1] * Mat[1][1] + k[2] * Mat[1][2] + k[3] *
Mat[1][3];
C = k[0] * Mat[2][0] + k[1] * Mat[2][1] + k[2] * Mat[2][2] + k[3] *
Mat[2][3];
D = k[0] * Mat[3][0] + k[1] * Mat[3][1] + k[2] * Mat[3][2] + k[3] *
Mat[3][3];
I still feel like there should be some minus signs in there to make the
interpolation work - but maybe those pop out the other side of the MInvers () .
.. . I'll have to write that out in SDL and run it to find out.
I also don't quite understand why we need to take the square root of the result
in line 1082
x[n] = sqrt(r[n] * (r[n] * (r[n] * A + B) + C) + D);
to get the interpolated spline values, but perhaps that may become clear as I
find more bits of time here and the to properly focus on this.
Just wanted to issue a progress report. :)
- BE
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"Bald Eagle" <cre### [at] netscapenet> wrote:
> I still feel like there should be some minus signs in there to make the
> interpolation work - but maybe those pop out the other side of the MInvers () .
> .. . I'll have to write that out in SDL and run it to find out.
Sent values of A-D for each segment to the debug stream, and there are
definitely minus signs.
> I also don't quite understand why we need to take the square root of the result
> in line 1082
> x[n] = sqrt(r[n] * (r[n] * (r[n] * A + B) + C) + D);
> to get the interpolated spline values, but perhaps that may become clear as I
> find more bits of time here and the to properly focus on this.
This apparently has to do with the value of "alpha" in the interpolation, with 0
being Uniform, 1/2 being Centripetal, and 1 being Chordal.
I'm not really sure where "r" comes from in the source, or how that while loop
interpolates the spline, but I just ignored all of that, and things worked out
anyway. :D
After fixing some boneheaded visualization bugs, the math seemed to be working
out with the spline, so I took my SDL version of the SOR spline and used the X
value (minus the minor radius) as the major radius of a torus, and "plotted" a
torus at each interpolation point. (RED)
Seems to overlay the sor {} object (BLUE) very closely. Errors are probably due
to my janky simulation method, and coincident surfaces.
I'll try to work out the details as I write things up, and I'll probably make a
parametric {} and isosurface {} object to further test how well things match up.
- BE
Post a reply to this message
Attachments:
Download 'surface of revolution documentation.png' (255 KB)
Preview of image 'surface of revolution documentation.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
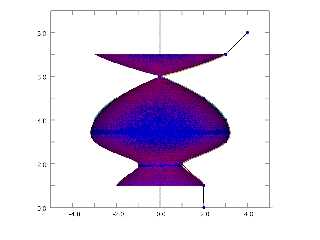
"Bald Eagle" <cre### [at] netscapenet> wrote:
> ... I'll probably make a
> parametric {} and isosurface {} object to further test how well things match up.
So this is the isosurface version, overlaid on the POV-Ray sor {} object
object {SOR scale 0.999999}
(It's actually one isosurface for every individual segment of the CR spline)
If I scale to 5 nines, I get a LOT more coincident surface artefacts, so I'd say
that everything is working very nicely.
I would still like to see that original 1989 paper, and perhaps I can work out
the square root thing with some level of rigor.
I'm pretty happy with what I've got, and will get working on some sort of
write-up.
If anyone has any questions, or would like to see a specific type of render,
animation, or mathematical derivation, just let me know, so I can include that.
- BE
Post a reply to this message
Attachments:
Download 'surface of revolution documentation.png' (80 KB)
Preview of image 'surface of revolution documentation.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
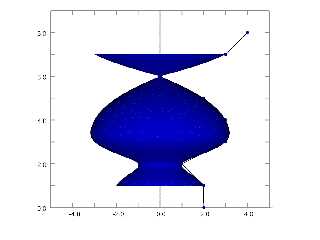
So, in the course of making some documentation renders, it became apparent that
there were a few things that were puzzling, needed to be sorted out, and some of
that was related to the behaviour of other keywords.
The following is a summary:
sor {} can have control points ON the axis, just not crossing it.
Else you get a "Parse Error: Incorrect point in surface of revolution"
I believe this is hard-coded behaviour in the source algorithm.
If I were to edit the source, it would allow the first and last control points
to cross the axis, since those points only exist to calculate the tangent
direction.
I do recall discussing this briefly in a thread with clipka and suggesting to
use abs {} somewhere in the algorithm, but I'd have to familiarize myself more
deeply with the specifics of what is going on numerically.
When using the sor {] object as the "cutter" in a difference {}, I unexpectedly
got some interior_texture {} showing in the result. Strangely enough, when i use
sor {open} the interior_texture {} is NOT visible, and I only see the surface
texture {}
When cutting away from the sor {}, I see the expected result, though I haven't
pursued this to see what more complicated geometry / CSG yields.
According to the sor {} tutorial in the wiki:
https://wiki.povray.org/content/Documentation:Tutorial_Section_3#Surface_of_Revolution_Object
"First and last point from the list are used to determine slope at beginning and
end of curve and can be defined for any height."
However, I find that to not be the case.
Swapping the first and last control points causes a
"Parse Error: Incorrect point in surface of revolution"
But if I only set the LAST control point y value to zero, technically making the
spline double-back in the y-direction, everything works fine.
and finally on to what sparked this whole investigation off:
I wanted to make a render comparing sor{} with sor {open}, but I had a devil of
a time slicing the vase in half and seeing the interior.
jr managed to achieve the desired result using clipped_by
As shown, when I use cutaway_textures, I DON'T see the expected
interior_texture, but the surface texture {}. And when I use sor {open}, I do
not see a hollow infinitely thin surface, I get a solid object sliced in half.
So, I would say that there are problems with the sor {} caps, possibly with the
normal vector.
As shown in the bottom left, when I slice the sor {open} in half with a box, I
get an apparently solid object. This is of course counterintuitive to what the
user expects, even though the documentation cautions that the open version might
yield unexpected results when used in CSG. I would probably classify this
result as sufficiently unexpected as to warrant its classification as a bug, or
for an extended warning with the clipped_by solution to be added to the
documentation.
Futhermore, if the documentation implies that a sor is solid - just look at the
CSG results of difference {} - then clipped_by ought to give me what I'm seeing
as difference {} only with the interior_texture {} properly displayed.
Other things I notice are that there is some noisy "cruft" at the base of the
clipped_by object. I also see some of that at the bottom of the difference{}s.
The texture is a tiling with a color_map, and is uv_mapped onto the surface(s).
As you can see on the right side of the object, the pattern does not line up
properly at the edges. In the model below that, "top cp doubles back", I
changed the scaling of the tiling to an even number, and it now lines up.
I recall reading about properly scaling patterns so that make them fit, and that
of course employed the use of pi or tau to calculate the proper scaling. This
might be a worthwhile keyword to implement for uv-mapping, perhaps some sort of
"scaling warp". Likely to be pattern and direction dependent.
All objects are rendered with sturm.
Enjoy & Discuss.
- BE
Post a reply to this message
Attachments:
Download 'sor permutations.png' (130 KB)
Preview of image 'sor permutations.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
Same renderings, but of sor {open}
Post a reply to this message
Attachments:
Download 'sor open permutations.png' (133 KB)
Preview of image 'sor open permutations.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
"Bald Eagle" <cre### [at] netscapenet> wrote:
> As shown, when I use cutaway_textures, I DON'T see the expected
> interior_texture, but the surface texture {}. And when I use sor {open}, I do
> not see a hollow infinitely thin surface, I get a solid object sliced in half.
Also, I'm curious as to why the cutaway_textures feature requires the use of an
untextured object as a cutter to be able to function properly.
One would reasonably expect that we should be able to use any object.
If, as per wiki documentation, the cutaway_textures feature result is based on
insidedness tests, then the texture of the cutter should be irrelevant.
- BE
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 9/7/25 12:10, Bald Eagle wrote:
> According to the sor {} tutorial in the wiki:
> https://wiki.povray.org/content/
> Documentation:Tutorial_Section_3#Surface_of_Revolution_Object
> "First and last point from the list are used to determine slope at beginning and
> end of curve and can be defined for any height."
>
> However, I find that to not be the case.
> Swapping the first and last control points causes a
> "Parse Error: Incorrect point in surface of revolution"
> But if I only set the LAST control point y value to zero, technically making the
> spline double-back in the y-direction, everything works fine.
First, Are you using v3.8 beta 2 for all your testing?
Second, Did you take care when you did the differences with the box to
not have coincident surfaces with the caps (if there) or that y height
when the caps are not there?
As to the point above, I don't see what you see. The following list
works for me where I have flipped / crossed the first and last control
points(*). See the attached image where the first is magenta and the
last is yellow.
<+1.5,+1.1> // C0
<+0.4,0.0> // C1
<+0.3,0.5> // C2
<+0.4,0.9> // C3
<+1.5,+0.1> // C4
I'll try and look at some of the other issues you mention as I have
time; Including temporarily removing the x>0.0 restriction on the first
and last points to see what happens. Aside: we did remove a similar
restriction for the lathe for v3.8 vs v3.7.
(*) I tried inverting all the on curve points and this does NOT work as
I incorrectly remembered for some recent sor{} post - that must be a
lathe{} only thing.
Bill P.
Post a reply to this message
Attachments:
Download 'be_sor01.png' (12 KB)
Preview of image 'be_sor01.png'
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 9/8/25 07:08, Bald Eagle wrote:
> "Bald Eagle" <cre### [at] netscapenet> wrote:
>
>> As shown, when I use cutaway_textures, I DON'T see the expected
>> interior_texture, but the surface texture {}. And when I use sor {open}, I do
>> not see a hollow infinitely thin surface, I get a solid object sliced in half.
>
> Also, I'm curious as to why the cutaway_textures feature requires the use of an
> untextured object as a cutter to be able to function properly.
> One would reasonably expect that we should be able to use any object.
> If, as per wiki documentation, the cutaway_textures feature result is based on
> insidedness tests, then the texture of the cutter should be irrelevant.
>
> - BE
>
>
>
Answering without thinking much, I don't think the cutaway_textures
feature copies the inside texture(*), but maybe I'm not remembering
correctly.
A reminder the yuqk fork fixed a cutaway_textures bug which exists in
official POV-Ray releases. See:
https://news.povray.org/povray.bugreports/thread/%3C65806257%241%40news.povray.org%3E/
Bill P.
(*) - The inside_texture{}s feature has a few inconsistencies, besides,
with respect to how texture{}s are handled.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
| |
|
|
On 9/8/25 10:04, William F Pokorny wrote:
> Answering without thinking much,
Ah, and to quote Alain:
"When using cutaway_texture, the object used to cut away part of the
rest must NOT have any texture."
Unsure your set up with respect to the particular post, but the overall
images suggest both the box and sor might have textures ?
Bill P.
Post a reply to this message
|
|
| |
| |
|
|
|
|
| |
|
|
