|
 |
Hello crazy people who continue to read me! However I am happy you are
here.
A) Determining more accurate scattering color
---------------------------------------------
In the previous post
(http://news.povray.org/povray.binaries.tutorials/thread/%3Cop.utj6u4lym1sclq%40pignouf%3E/
on May 7th), we played with some atmosphere parameters: elevation of the
sun, altitude of the camera, the density power factor ('k' in
d=Dmax*exp(-k*h/T)).
Now, there is another parameter which is worth to focus on: the rayleigh
scattering color. TerraPOV follows the physical property of Rayleigh
scattering which is wavelength dependent and is proportional to the 4th
power of the ratio of the wavelengths, most scattering being short
wavelengths (explaining blue sky). TerraPOV uses 3 'equivalent'
wavelengths for red, green, and bue. Most of you know that RGB are related
to the color spectrum of screen phospors and to human eye perception. So
it is not physically correct to make 3 single wavelengths correpond to the
RGB primaries. But we can try to determine better wavelengths that fit
observation closer.
For the first posts, I determined them using a CIExy chart with sRGB color
space and D65 white point I found on the web. I applied a ruler on the
screen from D65 to R, G, and B primaries successively and see the
intersection with the monochromatic locus. I got:
R --> 650 nm
G --> 555 nm
B --> 460 nm
giving the scattering color rgb <0.2508, 0.4719, 1.0000>.
That was a start point for the model. But, as we'll see below, the
saturation of the sky color is too low.To go further, I put CIE 1931 Color
Matching Function values in a spread sheet and re-calculated the
monochromatic locus and the coordinates of RGB primaries in that context.
With a precise chart, and 3 thin lines drawn from D65 to monocromatic
locus through the 3 primaries. I got another set of values:
R --> 612 nm
G --> 549 nm
B --> 465 nm
giving the scattering color rgb <0.3333, 0.5147, 1.0000>.
In fact, those values obtained using the 4th power of the wavelength
ratios are not really a color, but rather a set of relative scattering
factors, normalized to blue. The behaviour is quite visually acceptable
because it follows the basic physics rule (4th power).
Now, let's get into the color world. We take the previous 3 wavelengths
and determine their RGB equivalent using the xyz -> RGB transformation
(which can have negative values for red and green), and linear
interpolation:
612 nm --> rgb <1.671473, -0.049618, 0.152247>
549 nm --> rgb <-0,290579, 1.499741, 0,233735>
465 nm --> rgb <-0.0333144, -0.0412474, 1.6444632>
We apply the relative factors and we get:
C = 0.3333*<1.671473, -0.049618, 0.152247>
+ 0.5147*<-0,290579, 1.499741, 0,233735>
+ 1.0000*<-0.0333144, -0.0412474, 1.6444632> = <0.3742, 0.7141, 1.8155>
And if we normalize to blue (remember, the TP_RAYLEIGH_AMOUNT variable is
a multiplying factor defaulted to 1), we get:
#declare TP_RAYLEIGH_SCATTERING_COLOR = rgb <0.2061, 0.3933, 1.0>;
Surprisingly, this is very close to a simple rgb <0.2, 0.4, 1>.
It appears that the wavelengths are no more very useful: TP_LAMBDA_RED,
TP_LAMBDA_GREEN, and TP_LAMBDA_BLUE are removed. This value is our new
start point.
B) Checking colors
------------------
In order to check colors, we need to have our screen calibrated. Without
devices and sepcialized software, one may visit the
http://www.lagom.nl/lcd-test pages. This being done, we need to see what
happens in all the sky sphere. We need a fisheye camera. Let's make
TerraPOV provide several cameras. So we implement variables to chose which
camera we want:
// Cameras
#declare TP_DEFAULT_CAMERA = 0;
#declare TP_FISHEYE_CAMERA = 1;
#declare TP_CAMERA = TP_FISHEYE_CAMERA;
#declare TP_FISHEYECAM_HEIGHT = 0.5*m;
#declare _tp_fisheye_camera = camera
{
location 0
angle 180
right x*image_width/image_height
look_at z
rotate -90*x
rotate 180*y // To make the sun raise at the bottom of the image
translate TP_FISHEYECAM_HEIGHT *y
}
#switch(TP_CAMERA )
#case (TP_DEFAULT_CAMERA)
camera {_tp_default_camera}
#break
#case (TP_FISHEYE_CAMERA)
camera {_tp_fisheye_camera}
#break
#else
camera {_tp_default_camera}
#break
#end
The picture Skydome_rgb_0.2061_0.3933_1.0.png illustrates the situation
for -5, -1, 1, 5, 20 and 70 deg elevation. Not so bad. We just notice that
we have saturation of light near the horizon for intermediate elevations
(20°).Increasing sampling (intervals and samples) for a better integration
reduces this effect.
What will be our criteria for tuning colors at the stage we are now? I
take 2 objective and quantizable parameters, and one subjective. The first
two are the color of the sky and lightness of a white ground with 90¦
elevation sun, the subjective criterion is the behaviour at low elevation
and whether or not it looks realistic (remembering we still are in a pure
atmosphere with air molecules only and with rayleigh scattering only).
Criterion #1: Color of the sky: Hue, Saturation, and Lightness. Somebody
called Zawischa from Hannover university wrote a paper on scattering and
sky colors, see
http://www.itp.uni-hannover.de/~zawischa/ITP/scattering.html. He computed
the theoretical color of the sky due to Rayleigh scattering, and I'll
trust him:
Hue: 0.6
Saturation: 0.533
Lightness: 0.7
Let's try to get those values for a 90° elevation sun near the zenith.
Criterion #2: A 100% white ground with 100% diffuse appears 100% bright
for a 90° elevation sun. The white light from our sun passing through a
Rayleigh scattering media cannot produce white color on the ground. Never
mind, that will be part of next step. For now, our goal is to approach
these desired value as much as we can, and see what happens.
Criterion #3: Sunsets must appear natural.
All seen from ground level, of course.
We have at our disposal the scattering amount (defaulted to 1 for the
moment), the Dmax of the atmosphere, the brightness of the sun (defaulted
to 1 for the moment), and the scattering color of the media.
I sampled methodically a sufficiently wide domain for those parameters, I
put the values obtained in a spreadsheet, and I could draw the following
conclusions:
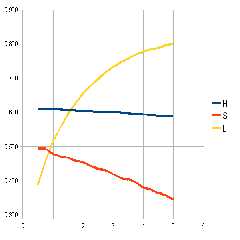
- Increasing the scattering amount, increases lightness, and descreases
saturation. In our case, we are always in the first part of the scattering
amount/lightness curve. This is shown by figure
IncreasingAmount_rgb_0.2_0.4_1.0.png. If we continue to increase the
amount, the attenuation will prevail and the curve will bend until it gets
a negative slope that reaches the x-axis asymptotically.
- Increasing Red decreases mainly saturation
- Increasing Green decreases mainly hue
- Increasing brightness simply increases lightness
I varied the scattering amount from 0.5 to 5 by 0.25 step with default
values for other prarameters, with scattering color rgb <0.2, 0.4, 1.0>. I
varied red from 0.5 to 2, and green from 0.2 to 0.6, both with 0.05 step.
I chose the values that corresponded best and tweaked by hand the
scattering color.
I ended up with those values and the second series of skies
Skydomes_bestrayleigh.png.
Amount = 2.3
Scattering color = rgb <0.135, 0.33, 1>
Brightness = 1/0.95 = 1.0526
Sky color at zenith, sun 90° elevation = hsl <0.6, 0.533, 0.698>
Ground color = rgb <0.996, 0.965, 0.855> = hsl <0.128, 0.141, 0.996>
Ground Brighness = 0.996
Interpretation
--------------
- Amount: We cannot use the brightness parameter to increase the
brightness of the sky, otherwise the ground will be saturated too quickly.
So we must use the scattering amount parameter.
- Scattering color: the rgb values for the scattering color correspond to
the following wavelengths, taking green as reference:
Red --> 686 nm
Green --> 549 nm
Blue --> 416 nm
The spectrum has been widened. This is because, in reality, our eyes
percieve also shorter and longer wavelengths. Those values take into
account what happens perceptually at both ends of the spectrum. Without
being really aware of it, we performed an integration of those wavelengths
with the Color Matching Functions. However the integrated spectrum is
considered as uniform (rgb 1). Witout this, we could NEVER reach the
saturation we wanted. So it's OK for our first objective criterion.
For the 3rd criterion, sunsets look obviously too greenish, and we have a
yellow color at 5° elevation and still a little at 20°, which is not very
realistic. This is due to the high scattering amount value of 2.3.
What about the second criterion, color of the ground? As mentionned above,
the white rgb 1 light of our sun cannot yield white color on the ground
because it lost more blue than red by travelling through the atmosphere.
The problem comes from sRGB assumptions and sun's real irradiance
spectrum. Until now, our model does not match the sRGB assumptions: the
light is rgb 1 at GROUND LEVEL with real values and the D65 white point is
the color defined considering clear sky under so-called 'standard'
conditions. That's why we cannot meet both objective criteria, nor is the
subjective criterion met. We'll have to deal with sun's spectrum above the
atmosphere, sun's spectrum on the ground. The difference is what is
absorbed.
So, WTF? Can't we have it all?
Our model needs new features: taking spectra into account (white ground,
good sky color, good lighness without a high amount of scttering), and
absorption (ozone: less greenish sunsets). I hope we can have it all ...
Next post will deal with spectra and absorption: TerraPOV - Sky system -
Atmosphere - Part5, An advanced model
Perhaps there will be some survivors to read me ...
Bruno
PS: The code for today:
#include "colors.inc"
#include "consts.inc"
global_settings
{
#if (version < 3.7) assumed_gamma 1 #end
max_trace_level 20
}
// Units
#declare m = 0.1; // A value of 1 makes the sun's distance ouside POV's
numerical domain.
#declare km = 1000*m;
#declare mm = 0.001*m;
// -----------------
// -- | Builtin enums | ------
// -----------------
// Cameras
#declare TP_DEFAULT_CAMERA = 0;
#declare TP_FISHEYE_CAMERA = 1;
// -------------
// -- | Parameters | ------
// -------------
// Camera
#declare TP_CAMERA = TP_FISHEYE_CAMERA;
// Earth parameters
#declare TP_EARTH_RADIUS = 6378.137*km;
// Sun parameters
#declare TP_SUN_HEADING = 0;
#declare TP_SUN_ELEVATION = 70;
#declare TP_BRIGHTNESS = 1/0.95;
#declare TP_SUN_COLOR = White;
#declare TP_SUN_APPARENT_APERTURE = 0.5; // Commonly admitted value
// Atmosphere parameters
#declare TP_ATMO_BOTTOM = -1*m;
#declare TP_RAYLEIGH_FACTOR = 1.0;
#declare TP_RAYLEIGH_DENSITY_MAX = 1;
#declare TP_RAYLEIGH_AMOUNT = 2.3;
#declare TP_ATMO_INTERVALS = 5; // Necessary for good integration
#declare TP_ATMO_SAMPLES = 5;
#declare TP_ATMO_METHOD = 3;
// Default camera parameters
#declare TP_DEFCAM_HEIGHT = 2*m; // Let's be tall
#declare TP_DEFCAM_HEADING = 0;
#declare TP_DEFCAM_ELEVATION = -90; // Let's look up a little
#declare TP_DEFCAM_ANGLE = 60;
// Fisheye camera prameters
#declare TP_FISHEYECAM_HEIGHT = 0.5*m;
// -------------
// -- | Engine | ------
// -------------
// Earth
#declare _tp_earth = sphere
{
0, TP_EARTH_RADIUS
pigment {White} // Could be any predefined texture, but normally, the
terrain hides the sphere
finish {ambient 0 diffuse 1}
translate -TP_EARTH_RADIUS*y
}
// Sun
#declare TP_SUN_DISTANCE = 10*TP_EARTH_RADIUS; // Far enough. Actual
distance in the scene is not very critical, as the light ays are parallel
#declare TP_SUN_RADIUS =
TP_SUN_DISTANCE*tan(radians(TP_SUN_APPARENT_APERTURE/2));
#declare _tp_basic_sun = light_source
{
<0, 0, 0>
color rgb TP_SUN_COLOR*TP_BRIGHTNESS
looks_like {sphere{0, TP_SUN_RADIUS pigment{Yellow} finish {diffuse 0
ambient 1}}}
translate TP_SUN_DISTANCE*z
parallel point_at -z
rotate -TP_SUN_ELEVATION*x
rotate TP_SUN_HEADING*y
}
// Atmosphere: density
#declare TP_BASE_RAYLEIGH_POWER = 6.7; // Constant
#declare _tp_rayleigh_power = TP_BASE_RAYLEIGH_POWER*TP_RAYLEIGH_FACTOR;
#declare TP_ATMO_THICKNESS = 50*km;
#declare _tp_rayleigh_density = density
{
function
{
TP_RAYLEIGH_DENSITY_MAX*exp(-_tp_rayleigh_power*(sqrt(x*x+(y+TP_EARTH_RADIUS)*(y+TP_EARTH_RADIUS)+z*z)
- TP_EARTH_RADIUS - TP_ATMO_BOTTOM)/TP_ATMO_THICKNESS)
}
}
// Atmosphere: scattering color
//#declare TP_RAYLEIGH_SCATTERING_COLOR = rgb
<pow(TP_LAMBDA_BLUE/TP_LAMBDA_RED, 4), pow(TP_LAMBDA_BLUE/TP_LAMBDA_GREEN,
4), 1>;
//#declare TP_RAYLEIGH_SCATTERING_COLOR = rgb <0.2061, 0.3933, 1.0>;
#declare TP_RAYLEIGH_SCATTERING_COLOR = rgb <0.135, 0.33, 1>;
// Atmosphere: media
#declare _tp_rayleigh_media = media
{
method TP_ATMO_METHOD
intervals TP_ATMO_INTERVALS
samples TP_ATMO_SAMPLES
scattering
{
RAYLEIGH_SCATTERING
color TP_RAYLEIGH_AMOUNT*TP_RAYLEIGH_SCATTERING_COLOR/TP_ATMO_THICKNESS
extinction 1 // The only physically accurate value
}
density {_tp_rayleigh_density}
}
// Atmosphere: shell
#declare _tp_rayleigh_atmosphere = difference
{
sphere {0, TP_EARTH_RADIUS + TP_ATMO_BOTTOM + TP_ATMO_THICKNESS
translate -TP_EARTH_RADIUS*y}
sphere {0, TP_EARTH_RADIUS + TP_ATMO_BOTTOM translate
-TP_EARTH_RADIUS*y}
hollow
pigment {rgbt 1}
interior {media{_tp_rayleigh_media}}
}
// Default camera
#declare _tp_default_camera = camera
{
location 0
angle TP_DEFCAM_ANGLE
right x*image_width/image_height
look_at z
rotate -TP_DEFCAM_ELEVATION*x
rotate TP_DEFCAM_HEADING*y
translate TP_DEFCAM_HEIGHT*y // Could use trace() to make sure we are
above the surface. But no terrain yet ...
}
// Fisheye camera
#declare _tp_fisheye_camera = camera
{
fisheye
location 0
angle 180
right x*image_width/image_height
look_at z
rotate -90*x
translate TP_FISHEYECAM_HEIGHT*y
}
// Scene
object {_tp_earth}
object {_tp_rayleigh_atmosphere}
object {_tp_basic_sun}
#switch(TP_CAMERA )
#case (TP_DEFAULT_CAMERA)
camera {_tp_default_camera}
#break
#case (TP_FISHEYE_CAMERA)
camera {_tp_fisheye_camera}
#break
#else
camera {_tp_default_camera}
#break
#end
--
Utilisant le client e-mail révolutionnaire d'Opera :
http://www.opera.com/mail/
Post a reply to this message
Attachments:
Download 'skydome_rgb_0.2061_0.3933_1.0.png' (854 KB)
Download 'increasingamount_rgb_0.2_0.4_1.0.png' (17 KB)
Download 'skydomes_bestrayleigh.png' (860 KB)
Preview of image 'skydome_rgb_0.2061_0.3933_1.0.png'

Preview of image 'increasingamount_rgb_0.2_0.4_1.0.png'
Preview of image 'skydomes_bestrayleigh.png'

|
 |




![]()