 |
 |
|
 |
|
 |
|  |
|  |
|
 |
From: Alain Martel
Subject: Re: Isosurface from magnitude of complex function with domain coloring
Date: 26 Dec 2021 12:32:39
Message: <61c8a737$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Le 2021-12-25 à 19:17, Tor Olav Kristensen a écrit :
> Alain Martel <kua### [at] videotron ca> wrote:
>> Le 2021-12-22 à 19:34, BayashiPascal a écrit :
>>> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail ca> wrote:
>> Le 2021-12-22 à 19:34, BayashiPascal a écrit :
>>> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>>>> ...
>>>> And yesterday I made some functions that can be used for HSV-coloring of
>>>> pigments.
>>>> ...
>>>
>>> The "multi-layered" aspect of the result is intriguing me. Does it come from a
>>> property of the function you've choosen, or from the way you choose to visualise
>>> it ?
>>> ...
>> Do you mean the repeating gradient ?
>> It comes from the way the «V» of the HSV value is computed, and values
>> larger than 1 get their integer part zeroed.
>>
>> Then, it's mapped to a 0..0.5 range.
>>
>> It could look something like this :
>> colour_map{
>> [0 hsv2rgb(<Hvalue, 1, 0>)]
>> [1 hsv2rgb(<Hvalue, 1, 0.5>)]
>> }
>
> Sorry Alain. I made a mistake and wrote "HSV-coloring" above. I meant to write
> "HSL-coloring". (I haven't yet looked at how HSV formulas works.)
>
> Also see my answer to Pascal in my previous post.
>
> --
> Tor Olav
> http://subcube.com
> https://github.com/t-o-k
>
>
The HSV and HSL colour spaces are almost the same. The «V» component in
HSV does pretty much the same as the «L» in HSL. com> wrote:
>>>> ...
>>>> And yesterday I made some functions that can be used for HSV-coloring of
>>>> pigments.
>>>> ...
>>>
>>> The "multi-layered" aspect of the result is intriguing me. Does it come from a
>>> property of the function you've choosen, or from the way you choose to visualise
>>> it ?
>>> ...
>> Do you mean the repeating gradient ?
>> It comes from the way the «V» of the HSV value is computed, and values
>> larger than 1 get their integer part zeroed.
>>
>> Then, it's mapped to a 0..0.5 range.
>>
>> It could look something like this :
>> colour_map{
>> [0 hsv2rgb(<Hvalue, 1, 0>)]
>> [1 hsv2rgb(<Hvalue, 1, 0.5>)]
>> }
>
> Sorry Alain. I made a mistake and wrote "HSV-coloring" above. I meant to write
> "HSL-coloring". (I haven't yet looked at how HSV formulas works.)
>
> Also see my answer to Pascal in my previous post.
>
> --
> Tor Olav
> http://subcube.com
> https://github.com/t-o-k
>
>
The HSV and HSL colour spaces are almost the same. The «V» component in
HSV does pretty much the same as the «L» in HSL.
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Cousin Ricky
Subject: Re: Isosurface from magnitude of complex function with domaincoloring
Date: 26 Dec 2021 20:43:03
Message: <61c91a27@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 2021-12-26 13:32, Alain Martel wrote:
>>
> The HSV and HSL colour spaces are almost the same. The «V» component in
> HSV does pretty much the same as the «L» in HSL.
That depends on what you mean by "pretty much the same." (There was an
argument on Usenet about 20-ish years ago over exactly this term
regarding pointers vs. arrays in C. I commented that I once blew a job
interview for tacitly considering them "pretty much the same.") I'm
amused that you're saying this on a thread by the same person who
schooled us on the difference between points and vectors.
The difference between L and V actually changes the meaning of
saturation between HSL and HSV. Michael Horvath gives a pretty good
visualization here:
https://github.com/LeForgeron/PovContributions/blob/master/colorsolid/sharkd%201.3.0/colorsolid.png
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
> On 26/12/2021 03:00, Tor Olav Kristensen wrote:
> >> ...
> >
> >> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
> >
> > ...
> >
> > I'm a bit worried though, because my renderings of that function is quite
> > different from mine.
>
> Sorry, I put the wrong picture :(
> here, it's the good one.
>
> > What is your rendering showing ?
> > The magnitude, the real part or the imaginary part ? - or something else ?
>
> let z = a + ib
> f(z) = c +i d
>
> Represented in POV in this way :
> a >> x axis
> b >> z axis
>
> arg(c + id) >> the color in HSL space with H = arg and L = logaritmic
> function of module between 0 and 1.
>
> module(c + id) >> y axis with a logarithmic scale
Ok, I see.
I've attached a similar rendering that I just I made of that function.
This time I've used used a mesh2 for the surface and added some black 1.5
degrees wide lines at 15 degrees intervals for the phase.
As you can see, the pole and the zeros seem to be located in a similar pattern,
but the area around the pole seems to be quite different.
I've tried to verify the functions I've created by feeding expressions to
Wolfram Alpha, like this:
https://www.wolframalpha.com/input/?i=%28-%283-4*i%29%5E3%2B%283-4*i%29%5E2*i%2B1%29%2F%28%283-4*i%29-1%2Bi%29%5E2
For the values of Z that I've tried, the results are the same as mine.
Perhaps you could do the same and compare with the results from your macros (?)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
> On 26/12/2021 03:00, Tor Olav Kristensen wrote:
> >> ...
> >
> >> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
> >
> > ...
> >
> > I'm a bit worried though, because my renderings of that function is quite
> > different from mine.
>
> Sorry, I put the wrong picture :(
> here, it's the good one.
>
> > What is your rendering showing ?
> > The magnitude, the real part or the imaginary part ? - or something else ?
>
> let z = a + ib
> f(z) = c +i d
>
> Represented in POV in this way :
> a >> x axis
> b >> z axis
>
> arg(c + id) >> the color in HSL space with H = arg and L = logaritmic
> function of module between 0 and 1.
>
> module(c + id) >> y axis with a logarithmic scale
Ok, I see.
I've attached a similar rendering that I just I made of that function.
This time I've used used a mesh2 for the surface and added some black 1.5
degrees wide lines at 15 degrees intervals for the phase.
As you can see, the pole and the zeros seem to be located in a similar pattern,
but the area around the pole seems to be quite different.
I've tried to verify the functions I've created by feeding expressions to
Wolfram Alpha, like this:
https://www.wolframalpha.com/input/?i=%28-%283-4*i%29%5E3%2B%283-4*i%29%5E2*i%2B1%29%2F%28%283-4*i%29-1%2Bi%29%5E2
For the values of Z that I've tried, the results are the same as mine.
Perhaps you could do the same and compare with the results from your macros (?)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'klps function.png' (396 KB)
Preview of image 'klps function.png'
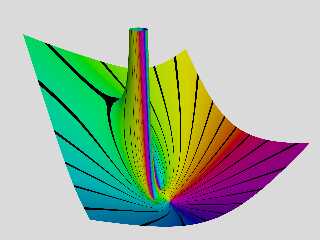
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> kurtz le pirate <kur### [at] gmail com> wrote:
> kurtz le pirate <kur### [at] gmail com> wrote:
> ...
> > module(c + id) >> y axis with a logarithmic scale
>
> Ok, I see.
What I did not notice was that you've used a logarithmic scale for y-axis.
That could explain the differences. Sorry.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
> ...
> > module(c + id) >> y axis with a logarithmic scale
>
> Ok, I see.
What I did not notice was that you've used a logarithmic scale for y-axis.
That could explain the differences. Sorry.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: kurtz le pirate
Subject: Re: Isosurface from magnitude of complex function with domain coloring
Date: 28 Dec 2021 10:10:28
Message: <61cb28e4@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 27/12/2021 03:46, Tor Olav Kristensen wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>> kurtz le pirate <kur### [at] gmail com> wrote:
>> kurtz le pirate <kur### [at] gmail com> wrote:
>> ...
>>> module(c + id) >> y axis with a logarithmic scale
>>
>> Ok, I see.
>
> What I did not notice was that you've used a logarithmic scale for y-axis.
>
> That could explain the differences. Sorry.
Yes, I used a logarithmic scale for this image.This is really not a good
idea. In fact the use of logarithms comes from my previous frameworks
for visualizing complex functions in 2D.
For the argument, it works fine. For the modulus, you have to take
precautions. Everything depends on the values of the functions you want
to plot. The growth at infinity can be very brutal and you lose a lot of
information with a linear scale ... that's why I used logs. But that was
for 2D ! In 3D now, no need for that.
Attached is my latest work with some cosmetic additions.
The represented function is :
f(z)= (sin(z) + cos(z)) / (z^2 - iz)
with Re and Im between -6 and +6.
--
Kurtz le pirate
Compagnie de la Banquise com> wrote:
>> ...
>>> module(c + id) >> y axis with a logarithmic scale
>>
>> Ok, I see.
>
> What I did not notice was that you've used a logarithmic scale for y-axis.
>
> That could explain the differences. Sorry.
Yes, I used a logarithmic scale for this image.This is really not a good
idea. In fact the use of logarithms comes from my previous frameworks
for visualizing complex functions in 2D.
For the argument, it works fine. For the modulus, you have to take
precautions. Everything depends on the values of the functions you want
to plot. The growth at infinity can be very brutal and you lose a lot of
information with a linear scale ... that's why I used logs. But that was
for 2D ! In 3D now, no need for that.
Attached is my latest work with some cosmetic additions.
The represented function is :
f(z)= (sin(z) + cos(z)) / (z^2 - iz)
with Re and Im between -6 and +6.
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
Attachments:
Download 'complex3dmesh_fn6.jpg' (91 KB)
Preview of image 'complex3dmesh_fn6.jpg'
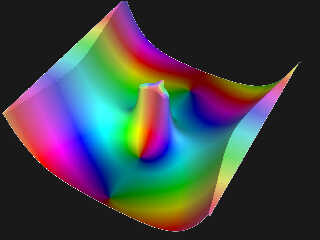
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
> On 27/12/2021 03:46, Tor Olav Kristensen wrote:
> > "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> On 27/12/2021 03:46, Tor Olav Kristensen wrote:
> > "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> >> kurtz le pirate <kur### [at] gmail com> wrote:
> >> kurtz le pirate <kur### [at] gmail com> wrote:
> >> ...
> >>> module(c + id) >> y axis with a logarithmic scale
> >>
> >> Ok, I see.
> >
> > What I did not notice was that you've used a logarithmic scale for y-axis.
> >
> > That could explain the differences. Sorry.
>
>
> Yes, I used a logarithmic scale for this image.This is really not a good
> idea. In fact the use of logarithms comes from my previous frameworks
> for visualizing complex functions in 2D.
>...
I have now made a couple of rendering of this function with both the natural
logarithm and the base 10 logarithm of the magnitude.
It looks like your rendering was done with the base 10 logarithm. The attached
rendering was done with the natural logarithm.
It seems to me that using a logarithmic scale can sometimes reveal some extra
information also in 3D.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
> >> ...
> >>> module(c + id) >> y axis with a logarithmic scale
> >>
> >> Ok, I see.
> >
> > What I did not notice was that you've used a logarithmic scale for y-axis.
> >
> > That could explain the differences. Sorry.
>
>
> Yes, I used a logarithmic scale for this image.This is really not a good
> idea. In fact the use of logarithms comes from my previous frameworks
> for visualizing complex functions in 2D.
>...
I have now made a couple of rendering of this function with both the natural
logarithm and the base 10 logarithm of the magnitude.
It looks like your rendering was done with the base 10 logarithm. The attached
rendering was done with the natural logarithm.
It seems to me that using a logarithmic scale can sometimes reveal some extra
information also in 3D.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'klps function _ ln.png' (244 KB)
Preview of image 'klps function _ ln.png'
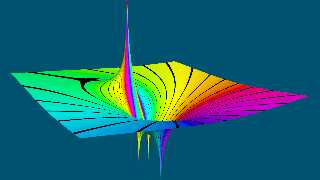
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
>...
> Attached is my latest work with some cosmetic additions.
> The represented function is :
> f(z)= (sin(z) + cos(z)) / (z^2 - iz)
> with Re and Im between -6 and +6.
That is a very nice looking function.
I really like the thin white edges and the small folds/bends at the ends.
The colors also seem to have a pleasant glow.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>...
> Attached is my latest work with some cosmetic additions.
> The represented function is :
> f(z)= (sin(z) + cos(z)) / (z^2 - iz)
> with Re and Im between -6 and +6.
That is a very nice looking function.
I really like the thin white edges and the small folds/bends at the ends.
The colors also seem to have a pleasant glow.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> Somehow, this makes me think of black hole gravity wells...
Yes, and when one plots the logarithm of the magnitude, like Kurtz le pirate
did, the zeros appear like those depicted wells.
> Intriguing!
=)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k org> wrote:
> Somehow, this makes me think of black hole gravity wells...
Yes, and when one plots the logarithm of the magnitude, like Kurtz le pirate
did, the zeros appear like those depicted wells.
> Intriguing!
=)
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Knowing partly what goes into all of this, I can see that it required a lot of
> time and attention to detail - and you always post fairly polished images, even
> if they are only WIPS.
Yes, it takes some time, but as long as it's interesting work I don't mind.
I seldom have time to polish finishes, textures or materials, so I mostly use
the default ones. But I do spend some time on the pigments and where to place
the light source and the camera.
> > I'm not very familier wit Paul Nylander's work. Those macros seem like a good
> > start for a library for complex calculations. But the Pow() macro could need
> > some work to allow for the exponent to also be a complex number.
>
> http://bugman123.com/index.html
Yes, I have seen his web pages some years ago, but I have never looked very
closely at them. They are quite "busy" with a layout that makes them a bit hard
to read - but they have many interesting topics. AFAIK he too lives in Norway.
> Complex exponents --- Oh, it makes my head hurt to even thing about that.
;-)
A^B = e^ln(A^B) = e^(B*ln(A))
pow(A, B) = exp(B*ln(A))
You already have formulas for complex exp() and multiplication - and
implementing ln() is not very hard.
> > I'm also wondering how hard it would be to use mod()
> > to have an infinite array of those "black hole vortices" on a plane - in either
> > a rectangular or an alternating/hexagonal arrangement...
>
> That's an interesting idea: to have a mod() operator that can handle complex
> values. But I don't know how to implement that...
Yes, that could be a way to create such repetitive patterns.
But it would be even better if a POV-Ray library could be made that can preserve
the repetitive nature of several of the complex operators (i.e. those that are
multi valued). I think that that would be quite hard to make...
> Maybe check out
> http://www.dimensions-math.org/Dim_E.htm
>
> and perhaps get in touch with the authors, since they seem to have an amazing
> grasp of both the math as well as POV-Ray.
That looks like an nice and interesting film. Thank you.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
> Knowing partly what goes into all of this, I can see that it required a lot of
> time and attention to detail - and you always post fairly polished images, even
> if they are only WIPS.
Yes, it takes some time, but as long as it's interesting work I don't mind.
I seldom have time to polish finishes, textures or materials, so I mostly use
the default ones. But I do spend some time on the pigments and where to place
the light source and the camera.
> > I'm not very familier wit Paul Nylander's work. Those macros seem like a good
> > start for a library for complex calculations. But the Pow() macro could need
> > some work to allow for the exponent to also be a complex number.
>
> http://bugman123.com/index.html
Yes, I have seen his web pages some years ago, but I have never looked very
closely at them. They are quite "busy" with a layout that makes them a bit hard
to read - but they have many interesting topics. AFAIK he too lives in Norway.
> Complex exponents --- Oh, it makes my head hurt to even thing about that.
;-)
A^B = e^ln(A^B) = e^(B*ln(A))
pow(A, B) = exp(B*ln(A))
You already have formulas for complex exp() and multiplication - and
implementing ln() is not very hard.
> > I'm also wondering how hard it would be to use mod()
> > to have an infinite array of those "black hole vortices" on a plane - in either
> > a rectangular or an alternating/hexagonal arrangement...
>
> That's an interesting idea: to have a mod() operator that can handle complex
> values. But I don't know how to implement that...
Yes, that could be a way to create such repetitive patterns.
But it would be even better if a POV-Ray library could be made that can preserve
the repetitive nature of several of the complex operators (i.e. those that are
multi valued). I think that that would be quite hard to make...
> Maybe check out
> http://www.dimensions-math.org/Dim_E.htm
>
> and perhaps get in touch with the authors, since they seem to have an amazing
> grasp of both the math as well as POV-Ray.
That looks like an nice and interesting film. Thank you.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>...
>
> I have now made a couple of rendering of this function with both the natural
> logarithm and the base 10 logarithm of the magnitude.
>
> It looks like your rendering was done with the base 10 logarithm. The attached
> rendering was done with the natural logarithm.
>
> It seems to me that using a logarithmic scale can sometimes reveal some extra
> information also in 3D.
Now my work with my POV-Ray library for complex functions has come a bit
further.
Here's an image where the domain colors for the function above are shown on a
plane. Here the lightness value for the colors are ramped up in intervals both
for the phase angle and the natural logarithm of the magnitude.
There are more images here for those that are interested:
https://github.com/t-o-k/POV-Ray-complex-functions
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>...
>
> I have now made a couple of rendering of this function with both the natural
> logarithm and the base 10 logarithm of the magnitude.
>
> It looks like your rendering was done with the base 10 logarithm. The attached
> rendering was done with the natural logarithm.
>
> It seems to me that using a logarithmic scale can sometimes reveal some extra
> information also in 3D.
Now my work with my POV-Ray library for complex functions has come a bit
further.
Here's an image where the domain colors for the function above are shown on a
plane. Here the lightness value for the colors are ramped up in intervals both
for the phase angle and the natural logarithm of the magnitude.
There are more images here for those that are interested:
https://github.com/t-o-k/POV-Ray-complex-functions
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'hueramps_magnramps.png' (493 KB)
Preview of image 'hueramps_magnramps.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()