 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"BayashiPascal" <bai### [at] gmail com> wrote:
>...
> Very nice.
>
> The "multi-layered" aspect of the result is intriguing me. Does it come from a
> property of the function you've choosen, or from the way you choose to visualise
> it ?
Thank you Pascal
The layered appearance is just a result from the coloring.
Here's how I did it:
#declare H_Fn =
function(re, im) {
degrees(mod(2*pi + ArgumentFn(re, im), 2*pi))
}
;
#declare S = 1.0;
#declare A = 0.6; // 0 < A < 1
#declare L_Fn =
function(re, im) {
mod(10*(1 - pow(A, MagnitudeFn(re, im))), 1)/2
}
;
isosurface {
function { y - MagnitudeFn(x, z) }
...
FunctionsPigmentRGB(
function { Rd_Fn(H_Fn(x, z), S, L_Fn(x, z)) },
function { Gn_Fn(H_Fn(x, z), S, L_Fn(x, z)) },
function { Bu_Fn(H_Fn(x, z), S, L_Fn(x, z)) }
)
}
In the attached image L_Fn() was changed to this:
#declare A = 0.2; // 0 < A < 1
#declare L_Fn =
function(re, im) {
(1 - pow(A, MagnitudeFn(re, im)))
}
;
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>...
> Very nice.
>
> The "multi-layered" aspect of the result is intriguing me. Does it come from a
> property of the function you've choosen, or from the way you choose to visualise
> it ?
Thank you Pascal
The layered appearance is just a result from the coloring.
Here's how I did it:
#declare H_Fn =
function(re, im) {
degrees(mod(2*pi + ArgumentFn(re, im), 2*pi))
}
;
#declare S = 1.0;
#declare A = 0.6; // 0 < A < 1
#declare L_Fn =
function(re, im) {
mod(10*(1 - pow(A, MagnitudeFn(re, im))), 1)/2
}
;
isosurface {
function { y - MagnitudeFn(x, z) }
...
FunctionsPigmentRGB(
function { Rd_Fn(H_Fn(x, z), S, L_Fn(x, z)) },
function { Gn_Fn(H_Fn(x, z), S, L_Fn(x, z)) },
function { Bu_Fn(H_Fn(x, z), S, L_Fn(x, z)) }
)
}
In the attached image L_Fn() was changed to this:
#declare A = 0.2; // 0 < A < 1
#declare L_Fn =
function(re, im) {
(1 - pow(A, MagnitudeFn(re, im)))
}
;
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
Attachments:
Download 'fivepoles_isosurface_otherlightness.png' (202 KB)
Preview of image 'fivepoles_isosurface_otherlightness.png'
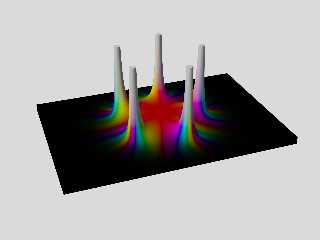
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Alain Martel <kua### [at] videotron ca> wrote:
> > "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail ca> wrote:
> > "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> >>...
> >> And yesterday I made some functions that can be used for HSV-coloring of
> >> pigments.
> >>...
> >
> > The "multi-layered" aspect of the result is intriguing me. Does it come from a
> > property of the function you've choosen, or from the way you choose to visualise
> > it ?
> >...
> Do you mean the repeating gradient ?
> larger than 1 get their integer part zeroed.
>
> Then, it's mapped to a 0..0.5 range.
>
> It could look something like this :
> colour_map{
> [0 hsv2rgb(<Hvalue, 1, 0>)]
> [1 hsv2rgb(<Hvalue, 1, 0.5>)]
> }
Sorry Alain. I made a mistake and wrote "HSV-coloring" above. I meant to write
"HSL-coloring". (I haven't yet looked at how HSV formulas works.)
Also see my answer to Pascal in my previous post.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
> >>...
> >> And yesterday I made some functions that can be used for HSV-coloring of
> >> pigments.
> >>...
> >
> > The "multi-layered" aspect of the result is intriguing me. Does it come from a
> > property of the function you've choosen, or from the way you choose to visualise
> > it ?
> >...
> Do you mean the repeating gradient ?
> larger than 1 get their integer part zeroed.
>
> Then, it's mapped to a 0..0.5 range.
>
> It could look something like this :
> colour_map{
> [0 hsv2rgb(<Hvalue, 1, 0>)]
> [1 hsv2rgb(<Hvalue, 1, 0.5>)]
> }
Sorry Alain. I made a mistake and wrote "HSV-coloring" above. I meant to write
"HSL-coloring". (I haven't yet looked at how HSV formulas works.)
Also see my answer to Pascal in my previous post.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Kenneth" <kdw### [at] gmail com> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>
> >
> > The colors are chosen so that the hue follows the phase (or argument) of the
> > function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> > axis. The saturation is 100% everywhere.
> >
>
> Those beautiful color gradations remind me of old-style blown-glass/metallic
> Christmas tree ornaments; it even appears as if they have blurred reflections.
> That's an amazing result. Nice!
Thank you Kenneth !
The nice color gradients resulting from the formulas was a surprise to me.
I don't think that I have seen such old style blown glass ornaments.
Are they like this ?
https://www.nordichouse.co.uk/vintage-bordeaux-glass-bauble-p-4022.html
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>
> >
> > The colors are chosen so that the hue follows the phase (or argument) of the
> > function, while the lightness goes from 0.0 to 0.5 in intervals along the height
> > axis. The saturation is 100% everywhere.
> >
>
> Those beautiful color gradations remind me of old-style blown-glass/metallic
> Christmas tree ornaments; it even appears as if they have blurred reflections.
> That's an amazing result. Nice!
Thank you Kenneth !
The nice color gradients resulting from the formulas was a surprise to me.
I don't think that I have seen such old style blown glass ornaments.
Are they like this ?
https://www.nordichouse.co.uk/vintage-bordeaux-glass-bauble-p-4022.html
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>...
> Very nice.
Thank you Bill !
> I was consulting the stuff that Paul Nylander wrote. I'm assuming yours are
> similar.
I'm not very familier wit Paul Nylander's work. Those macros seem like a good
start for a library for complex calculations. But the Pow() macro could need
some work to allow for the exponent to also be a complex number.
I did not create macros to do the calculations, but arrays of functions and
macros that assemble functions into new functions. For each complex operator
there's two functions; one for calculating the real part and one for calculating
the imaginary part.
>...
> I made these two to just keep track
>
> #macro Argument (Re, Im)
> atan2 (Re, Im)
> #end
>
> #macro Modulus (Re, Im)
> sqrt (pow (Re, 2) + pow (Im, 2))
> #end
I like your Modulus() macro better than the Abs() macro, because it does not
rely on the underlying implementation of how the complex numbers are
represented. I think that as few as possible of the macros should depend on the
underlying implementations. Btw.: Why have you chosen to have a different
atan2() call in your Argument() macro than in the Arg() macro ?
> I worked those out from the macros in colors.inc. A little challenging at first
> to turn that whole thing into a function. ;)
Yes, that's a bit of a struggle.
>...
> This is looking great! I'm sure there are a lot of other interesting complex
> surfaces to be explored.
I've started on a Github repository for my library. It's here:
https://github.com/t-o-k/POV-Ray-complex-functions
Please note that this is a work in progress, so some features hasn't been added
yet and much of it may change.
> I'm also wondering how hard it would be to use mod()
> to have an infinite array of those "black hole vortices" on a plane - in either
> a rectangular or an alternating/hexagonal arrangement...
That's an interesting idea: to have a mod() operator that can handle complex
values. But I don't know how to implement that...
--
Tor Olav
http://subcube.com
https://github.com/t-o-k net> wrote:
>...
> Very nice.
Thank you Bill !
> I was consulting the stuff that Paul Nylander wrote. I'm assuming yours are
> similar.
I'm not very familier wit Paul Nylander's work. Those macros seem like a good
start for a library for complex calculations. But the Pow() macro could need
some work to allow for the exponent to also be a complex number.
I did not create macros to do the calculations, but arrays of functions and
macros that assemble functions into new functions. For each complex operator
there's two functions; one for calculating the real part and one for calculating
the imaginary part.
>...
> I made these two to just keep track
>
> #macro Argument (Re, Im)
> atan2 (Re, Im)
> #end
>
> #macro Modulus (Re, Im)
> sqrt (pow (Re, 2) + pow (Im, 2))
> #end
I like your Modulus() macro better than the Abs() macro, because it does not
rely on the underlying implementation of how the complex numbers are
represented. I think that as few as possible of the macros should depend on the
underlying implementations. Btw.: Why have you chosen to have a different
atan2() call in your Argument() macro than in the Arg() macro ?
> I worked those out from the macros in colors.inc. A little challenging at first
> to turn that whole thing into a function. ;)
Yes, that's a bit of a struggle.
>...
> This is looking great! I'm sure there are a lot of other interesting complex
> surfaces to be explored.
I've started on a Github repository for my library. It's here:
https://github.com/t-o-k/POV-Ray-complex-functions
Please note that this is a work in progress, so some features hasn't been added
yet and much of it may change.
> I'm also wondering how hard it would be to use mod()
> to have an infinite array of those "black hole vortices" on a plane - in either
> a rectangular or an alternating/hexagonal arrangement...
That's an interesting idea: to have a mod() operator that can handle complex
values. But I don't know how to implement that...
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
kurtz le pirate <kur### [at] gmail com> wrote:
>...
> Very good job !
>
> The basic operators on the complexes is much more elaborate than mine. I
> use simple macros. This makes the definitions a little more difficult to
> work out. For example, for f(z) = z + 1/z, I have to write
> complexAdd(cc,complexInverse(cc)).
Yes, that's like a prefix notation, which is natural for such a macro library.
> The really interesting part is the use of isosurfaces. Good job. I just
> used colored triangles which give me a {} mesh. The coloring model is
> also very clever because the hue and luminosity depend on the value of
> the function.
Thank you. I'm glad that you like this Kurtz.
It wanted my library to also work with isosufaces and pigments, so I had to use
functions to do all the calculations.
I read about domain coloring with HSL-colors here:
https://en.wikipedia.org/wiki/Domain_coloring
> I will see how to add the same coloring scheme as you.
You could have a peek at my implementation here:
https://github.com/t-o-k/POV-Ray-complex-functions
> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
Here's how I have to enter that function in order to process it with my current
macros. It's a kind of postfix notation/implementation.
#declare No = 16;
#declare PartTypes = array[No];
#declare Arguments = array[No];
#declare PartTypes[0] = "Z";
#declare Arguments[0] = ZFn();
#declare PartTypes[1] = "Const";
#declare Arguments[1] = RealConstFn(+3.0);
#declare PartTypes[2] = "Pow";
#declare Arguments[2] = Arg2Fn(0, 1);
#declare PartTypes[3] = "Neg";
#declare Arguments[3] = Arg1Fn(2);
#declare PartTypes[4] = "Z";
#declare Arguments[4] = ZFn();
#declare PartTypes[5] = "Const";
#declare Arguments[5] = ImagConstFn(+1.0);
#declare PartTypes[6] = "Sqr";
#declare Arguments[6] = Arg1Fn(4);
#declare PartTypes[7] = "Mul";
#declare Arguments[7] = Arg2Fn(5, 6);
#declare PartTypes[8] = "Add";
#declare Arguments[8] = Arg2Fn(3, 7);
#declare PartTypes[9] = "Const";
#declare Arguments[9] = RealConstFn(+1.0);
#declare PartTypes[10] = "Add";
#declare Arguments[10] = Arg2Fn(8, 9);
#declare PartTypes[11] = "Z";
#declare Arguments[11] = ZFn();
#declare PartTypes[12] = "Const";
#declare Arguments[12] = ComplexConstFn(-1.0, +1.0);
#declare PartTypes[13] = "Add";
#declare Arguments[13] = Arg2Fn(11, 12);
#declare PartTypes[14] = "Sqr";
#declare Arguments[14] = Arg1Fn(13);
#declare PartTypes[15] = "Div";
#declare Arguments[15] = Arg2Fn(10, 14);
I'm a bit worried though, because my renderings of that function is quite
different from mine.
What is your rendering showing ?
The magnitude, the real part or the imaginary part ? - or something else ?
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>...
> Very good job !
>
> The basic operators on the complexes is much more elaborate than mine. I
> use simple macros. This makes the definitions a little more difficult to
> work out. For example, for f(z) = z + 1/z, I have to write
> complexAdd(cc,complexInverse(cc)).
Yes, that's like a prefix notation, which is natural for such a macro library.
> The really interesting part is the use of isosurfaces. Good job. I just
> used colored triangles which give me a {} mesh. The coloring model is
> also very clever because the hue and luminosity depend on the value of
> the function.
Thank you. I'm glad that you like this Kurtz.
It wanted my library to also work with isosufaces and pigments, so I had to use
functions to do all the calculations.
I read about domain coloring with HSL-colors here:
https://en.wikipedia.org/wiki/Domain_coloring
> I will see how to add the same coloring scheme as you.
You could have a peek at my implementation here:
https://github.com/t-o-k/POV-Ray-complex-functions
> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
Here's how I have to enter that function in order to process it with my current
macros. It's a kind of postfix notation/implementation.
#declare No = 16;
#declare PartTypes = array[No];
#declare Arguments = array[No];
#declare PartTypes[0] = "Z";
#declare Arguments[0] = ZFn();
#declare PartTypes[1] = "Const";
#declare Arguments[1] = RealConstFn(+3.0);
#declare PartTypes[2] = "Pow";
#declare Arguments[2] = Arg2Fn(0, 1);
#declare PartTypes[3] = "Neg";
#declare Arguments[3] = Arg1Fn(2);
#declare PartTypes[4] = "Z";
#declare Arguments[4] = ZFn();
#declare PartTypes[5] = "Const";
#declare Arguments[5] = ImagConstFn(+1.0);
#declare PartTypes[6] = "Sqr";
#declare Arguments[6] = Arg1Fn(4);
#declare PartTypes[7] = "Mul";
#declare Arguments[7] = Arg2Fn(5, 6);
#declare PartTypes[8] = "Add";
#declare Arguments[8] = Arg2Fn(3, 7);
#declare PartTypes[9] = "Const";
#declare Arguments[9] = RealConstFn(+1.0);
#declare PartTypes[10] = "Add";
#declare Arguments[10] = Arg2Fn(8, 9);
#declare PartTypes[11] = "Z";
#declare Arguments[11] = ZFn();
#declare PartTypes[12] = "Const";
#declare Arguments[12] = ComplexConstFn(-1.0, +1.0);
#declare PartTypes[13] = "Add";
#declare Arguments[13] = Arg2Fn(11, 12);
#declare PartTypes[14] = "Sqr";
#declare Arguments[14] = Arg1Fn(13);
#declare PartTypes[15] = "Div";
#declare Arguments[15] = Arg2Fn(10, 14);
I'm a bit worried though, because my renderings of that function is quite
different from mine.
What is your rendering showing ?
The magnitude, the real part or the imaginary part ? - or something else ?
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
>...
> #declare PartTypes[4] = "Z";
> #declare Arguments[4] = ZFn();
>
> #declare PartTypes[5] = "Const";
> #declare Arguments[5] = ImagConstFn(+1.0);
>
> #declare PartTypes[6] = "Sqr";
> #declare Arguments[6] = Arg1Fn(4);
>
> #declare PartTypes[7] = "Mul";
> #declare Arguments[7] = Arg2Fn(5, 6);
>
Oops.
I should have written those assignments like this:
#declare PartTypes[4] = "Const";
#declare Arguments[4] = ImagConstFn(+1.0);
#declare PartTypes[5] = "Z";
#declare Arguments[5] = ZFn();
#declare PartTypes[6] = "Sqr";
#declare Arguments[6] = Arg1Fn(5);
#declare PartTypes[7] = "Mul";
#declare Arguments[7] = Arg2Fn(4, 6);
- But the resulting functions would yield the same values.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k com> wrote:
>...
> #declare PartTypes[4] = "Z";
> #declare Arguments[4] = ZFn();
>
> #declare PartTypes[5] = "Const";
> #declare Arguments[5] = ImagConstFn(+1.0);
>
> #declare PartTypes[6] = "Sqr";
> #declare Arguments[6] = Arg1Fn(4);
>
> #declare PartTypes[7] = "Mul";
> #declare Arguments[7] = Arg2Fn(5, 6);
>
Oops.
I should have written those assignments like this:
#declare PartTypes[4] = "Const";
#declare Arguments[4] = ImagConstFn(+1.0);
#declare PartTypes[5] = "Z";
#declare Arguments[5] = ZFn();
#declare PartTypes[6] = "Sqr";
#declare Arguments[6] = Arg1Fn(5);
#declare PartTypes[7] = "Mul";
#declare Arguments[7] = Arg2Fn(4, 6);
- But the resulting functions would yield the same values.
--
Tor Olav
http://subcube.com
https://github.com/t-o-k
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> Thank you Pascal
>
> The layered appearance is just a result from the coloring.
Thank you ! Now my confusion is entirely cleared up. :-)
Pascal com> wrote:
> Thank you Pascal
>
> The layered appearance is just a result from the coloring.
Thank you ! Now my confusion is entirely cleared up. :-)
Pascal
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" <tor### [at] TOBEREMOVEDgmail com> wrote:
> "Kenneth" <kdw### [at] gmail com> wrote:
> "Kenneth" <kdw### [at] gmail com> wrote:
> >
> > Those beautiful color gradations remind me of old-style blown-glass/metallic
> > Christmas tree ornaments...
>
> I don't think that I have seen such old style blown glass ornaments.
These three examples come closest to what I remember seeing, when I was a kid
visiting my grandmother for the holidays...
https://www.pinterest.com/pin/210824826294535957/
https://www.pinterest.com/pin/645281452835747592/
https://www.pinterest.com/pin/550002173251947194/
.... but your colors are even better and more saturated. And you have managed to
capture that blurred metallic 'sheen'. It's probably an optical illusion, but
the effect is quite magical. com> wrote:
> >
> > Those beautiful color gradations remind me of old-style blown-glass/metallic
> > Christmas tree ornaments...
>
> I don't think that I have seen such old style blown glass ornaments.
These three examples come closest to what I remember seeing, when I was a kid
visiting my grandmother for the holidays...
https://www.pinterest.com/pin/210824826294535957/
https://www.pinterest.com/pin/645281452835747592/
https://www.pinterest.com/pin/550002173251947194/
.... but your colors are even better and more saturated. And you have managed to
capture that blurred metallic 'sheen'. It's probably an optical illusion, but
the effect is quite magical.
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: kurtz le pirate
Subject: Re: Isosurface from magnitude of complex function with domain coloring
Date: 26 Dec 2021 06:13:42
Message: <61c84e66$1@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 26/12/2021 03:00, Tor Olav Kristensen wrote:
>> ...
>
>> Here, one sample of f(z) = (-z^3 + iz^2 + 1) / (z - 1 + i)^2.
>
> ...
>
> I'm a bit worried though, because my renderings of that function is quite
> different from mine.
Sorry, I put the wrong picture :(
here, it's the good one.
> What is your rendering showing ?
> The magnitude, the real part or the imaginary part ? - or something else ?
let z = a + ib
f(z) = c +i d
Represented in POV in this way :
a >> x axis
b >> z axis
arg(c + id) >> the color in HSL space with H = arg and L = logaritmic
function of module between 0 and 1.
module(c + id) >> y axis with a logarithmic scale
--
Kurtz le pirate
Compagnie de la Banquise
Post a reply to this message
Attachments:
Download 'complex3dmesh_fn00.jpg' (82 KB)
Preview of image 'complex3dmesh_fn00.jpg'
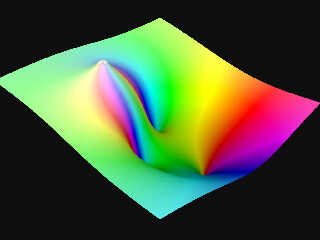
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Tor Olav Kristensen" wrote:
> Thank you Bill !
Knowing partly what goes into all of this, I can see that it required a lot of
time and attention to detail - and you always post fairly polished images, even
if they are only WIPS.
>
> I'm not very familier wit Paul Nylander's work. Those macros seem like a good
> start for a library for complex calculations. But the Pow() macro could need
> some work to allow for the exponent to also be a complex number.
http://bugman123.com/index.html
Complex exponents --- Oh, it makes my head hurt to even thing about that.
> I did not create macros to do the calculations, but arrays of functions and
> macros that assemble functions into new functions. For each complex operator
> there's two functions; one for calculating the real part and one for calculating
> the imaginary part.
Yes, since you are doing isosurfaces, it would have to be that way.
Not having done a great deal personally with complex math, I wasn't about to
start writing things from scratch, and wanted to just see what "known good code"
would spit out.
>
> >...
> > I made these two to just keep track
> >
> > #macro Argument (Re, Im)
> > atan2 (Re, Im)
> > #end
> >
> > #macro Modulus (Re, Im)
> > sqrt (pow (Re, 2) + pow (Im, 2))
> > #end
>
> I like your Modulus() macro better than the Abs() macro, because it does not
> rely on the underlying implementation of how the complex numbers are
> represented. I think that as few as possible of the macros should depend on the
> underlying implementations.
I was just working off of the definitions of the terms. Sometimes I mix and
match things without worrying about things too much, just to see what works
without overcomplicating things early on.
> Btw.: Why have you chosen to have a different
> atan2() call in your Argument() macro than in the Arg() macro ?
I believe the first one is Paul's, and the last one is one I wrote from scratch.
Again, just from definition of the term. If that gave rise to any "errors" - I
figured I could go back and fix them once I had some geometry rendered to
visually see what the problems were.
> > This is looking great! I'm sure there are a lot of other interesting complex
> > surfaces to be explored.
>
> I've started on a Github repository for my library. It's here:
> https://github.com/t-o-k/POV-Ray-complex-functions
>
> Please note that this is a work in progress, so some features hasn't been added
> yet and much of it may change.
Nice. That would probably be well suited to printing out and looking over
during coffee break.
> > I'm also wondering how hard it would be to use mod()
> > to have an infinite array of those "black hole vortices" on a plane - in either
> > a rectangular or an alternating/hexagonal arrangement...
>
> That's an interesting idea: to have a mod() operator that can handle complex
> values. But I don't know how to implement that...
Naive question: Wouldn't you just process the Re and Im parts with mod first
before passing them on to the subsequent functions?
Maybe check out
http://www.dimensions-math.org/Dim_E.htm
and perhaps get in touch with the authors, since they seem to have an amazing
grasp of both the math as well as POV-Ray.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()