 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
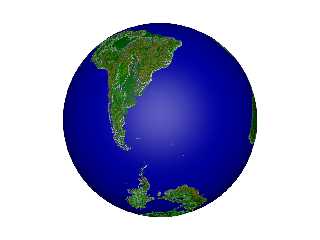
I have a hole at the South pole, ...
Here's a view of the Antarctic hole:
[which sounds highly inappropriate, I know, but...] net> wrote:
I have a hole at the South pole, ...
Here's a view of the Antarctic hole:
[which sounds highly inappropriate, I know, but...]
Post a reply to this message
Attachments:
Download 'sphericalheightfieldtest_spole.png' (247 KB)
Preview of image 'sphericalheightfieldtest_spole.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 21/07/2020 à 03:20, Bald Eagle a écrit :
> "Bald Eagle" <cre### [at] netscape net> wrote:
> I have a hole at the South pole, ...
>
> Here's a view of the Antarctic hole:
>
> [which sounds highly inappropriate, I know, but...]
>
acos( min( y / length, 1) ) : the clipping is done for the north pole,
but not the south pole (-1)
what about "acos(max(min(y/length, 1),-1)) ? net> wrote:
> I have a hole at the South pole, ...
>
> Here's a view of the Antarctic hole:
>
> [which sounds highly inappropriate, I know, but...]
>
acos( min( y / length, 1) ) : the clipping is done for the north pole,
but not the south pole (-1)
what about "acos(max(min(y/length, 1),-1)) ?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> acos( min( y / length, 1) ) : the clipping is done for the north pole,
> but not the south pole (-1)
>
> what about "acos(max(min(y/length, 1),-1)) ?
Thanks Jerome, it was a good suggestion, but the hole is still there.
I'm also concerned that although I may happen upon a "solution" that looks nice
graphically, it will be numerically wrong. And that's because I'm going to be
using these calculations to "look up" the altitude on the rectangular elevation
map in order to construct planet tiles that are in the right position (as
closely as possible using this method and the data available).
I'm also curious as to why I got I got a core dump with no clipping, and no core
dump with half-clipping, if the domain input was the underlying issue. Because
without the min(), then I'd be running into the same problem that I was
imagining was happening, only with the opposite sign.
And I'm not even sure that the domain was out range now that we're back into
this again. (it's early, before coffee, and it's HOT)
(I mean, can y ever exceed the vector length to give a quotient exceeding
unity?)
I DO have my isosurface contained by a sphere instead of a box - maybe that has
something to do with it - I will check later this afternoon.
I really do have a knack for finding these little hidden problems... fr> wrote:
> acos( min( y / length, 1) ) : the clipping is done for the north pole,
> but not the south pole (-1)
>
> what about "acos(max(min(y/length, 1),-1)) ?
Thanks Jerome, it was a good suggestion, but the hole is still there.
I'm also concerned that although I may happen upon a "solution" that looks nice
graphically, it will be numerically wrong. And that's because I'm going to be
using these calculations to "look up" the altitude on the rectangular elevation
map in order to construct planet tiles that are in the right position (as
closely as possible using this method and the data available).
I'm also curious as to why I got I got a core dump with no clipping, and no core
dump with half-clipping, if the domain input was the underlying issue. Because
without the min(), then I'd be running into the same problem that I was
imagining was happening, only with the opposite sign.
And I'm not even sure that the domain was out range now that we're back into
this again. (it's early, before coffee, and it's HOT)
(I mean, can y ever exceed the vector length to give a quotient exceeding
unity?)
I DO have my isosurface contained by a sphere instead of a box - maybe that has
something to do with it - I will check later this afternoon.
I really do have a knack for finding these little hidden problems...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 21/07/2020 à 12:58, Bald Eagle a écrit :
> Le_Forgeron <jgr### [at] free fr> wrote:
>
>> acos( min( y / length, 1) ) : the clipping is done for the north pole,
>> but not the south pole (-1)
>>
>> what about "acos(max(min(y/length, 1),-1)) ?
>
> Thanks Jerome, it was a good suggestion, but the hole is still there.
>
> I'm also concerned that although I may happen upon a "solution" that looks nice
> graphically, it will be numerically wrong. And that's because I'm going to be
> using these calculations to "look up" the altitude on the rectangular elevation
> map in order to construct planet tiles that are in the right position (as
> closely as possible using this method and the data available).
>
> I'm also curious as to why I got I got a core dump with no clipping, and no core
> dump with half-clipping, if the domain input was the underlying issue. Because
> without the min(), then I'd be running into the same problem that I was
> imagining was happening, only with the opposite sign.
>
> And I'm not even sure that the domain was out range now that we're back into
> this again. (it's early, before coffee, and it's HOT)
> (I mean, can y ever exceed the vector length to give a quotient exceeding
> unity?)
> I DO have my isosurface contained by a sphere instead of a box - maybe that has
> something to do with it - I will check later this afternoon.
>
> I really do have a knack for finding these little hidden problems...
>
>
For playing with geodesique coordinates in another life, my
recommendation is that you should avoid acos formula, as for position
near the pole the precision is about 1-x²/2, which means you are getting
compression of detail at the pole so strong that you cannot tell apart
two poins that are 100 m aways.
When distance between two points is to be computed, there is a
preference for the haversine formula instead of basic acos.
For your computation of latitude, you can use the complemented angle and
asin instead, then complement the result, using the sign of y as final
update.
The loss of precision near 0 is far "better" than the loss of precision
near 1, due to representation of floating point numbers.
#declare Latitude = pi/2 - asin( sqrt( x*x+z*z)/sqrt(x*x+y*y+z*z) );
#if (y<0)
#declare Latitude = -1 * Latitude;
#end fr> wrote:
>
>> acos( min( y / length, 1) ) : the clipping is done for the north pole,
>> but not the south pole (-1)
>>
>> what about "acos(max(min(y/length, 1),-1)) ?
>
> Thanks Jerome, it was a good suggestion, but the hole is still there.
>
> I'm also concerned that although I may happen upon a "solution" that looks nice
> graphically, it will be numerically wrong. And that's because I'm going to be
> using these calculations to "look up" the altitude on the rectangular elevation
> map in order to construct planet tiles that are in the right position (as
> closely as possible using this method and the data available).
>
> I'm also curious as to why I got I got a core dump with no clipping, and no core
> dump with half-clipping, if the domain input was the underlying issue. Because
> without the min(), then I'd be running into the same problem that I was
> imagining was happening, only with the opposite sign.
>
> And I'm not even sure that the domain was out range now that we're back into
> this again. (it's early, before coffee, and it's HOT)
> (I mean, can y ever exceed the vector length to give a quotient exceeding
> unity?)
> I DO have my isosurface contained by a sphere instead of a box - maybe that has
> something to do with it - I will check later this afternoon.
>
> I really do have a knack for finding these little hidden problems...
>
>
For playing with geodesique coordinates in another life, my
recommendation is that you should avoid acos formula, as for position
near the pole the precision is about 1-x²/2, which means you are getting
compression of detail at the pole so strong that you cannot tell apart
two poins that are 100 m aways.
When distance between two points is to be computed, there is a
preference for the haversine formula instead of basic acos.
For your computation of latitude, you can use the complemented angle and
asin instead, then complement the result, using the sign of y as final
update.
The loss of precision near 0 is far "better" than the loss of precision
near 1, due to representation of floating point numbers.
#declare Latitude = pi/2 - asin( sqrt( x*x+z*z)/sqrt(x*x+y*y+z*z) );
#if (y<0)
#declare Latitude = -1 * Latitude;
#end
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> Le 21/07/2020 à 12:58, Bald Eagle a écrit :
> > I'm also curious as to why I got I got a core dump with no clipping, and no core
> > dump with half-clipping, if the domain input was the underlying issue.
Can you test this in POV-Ray and HGpovray38 to see if you get an error?
> > And I'm not even sure that the domain was out range now that we're back into
> > this again.
> > (I mean, can y ever exceed the vector length to give a quotient exceeding
> > unity?)
I did a quick spreadsheet calculation. Aside from some numerical/binary
representation/rounding it shouldn't.
>... there is a
> preference for the haversine formula instead of basic acos.
Nice. That was an interesting read - thanks!
> For your computation of latitude, you can use the complemented angle and
> asin instead, then complement the result, using the sign of y as final
> update.
>
> The loss of precision near 0 is far "better" than the loss of precision
> near 1, due to representation of floating point numbers.
>
> #declare Latitude = pi/2 - asin( sqrt( x*x+z*z)/sqrt(x*x+y*y+z*z) );
> #if (y<0)
> #declare Latitude = -1 * Latitude;
> #end
I dabbled with all of that.
It was "wrong" at first - since sin is opposite over hypotenuse, and y would be
the cathetus opposite the angle, it should be y/vlength instead of sqrt(
x*x+z*z)/vlength ... yes?
Which is kinda just what I had before, only using asin with a 90-deg phase
shift.
And I got the exact same result.
Which was disappointing at first, but which I recognized held promise.
So, after coffee, shower, and kicking back for a bit (it was NOT a nap...) I
realized that if, perhaps, it wasn't the math - then it had to be what the math
was mapping.
[TdG will back me up on the merits of considering these things behind closed
eyes.]
If the image was getting mapped correctly, but there were extra pixels in the
image... And sure enough, comparing the elevation map to a different image map
showed that there is indeed a strip of pixels where there ought be none.
Damn it.
Stupid assumptions...
"We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time...."
Thanks for spinning me around in this circle one more time, Jerome. :)
Now maybe I can make some actual meaningful progress... fr> wrote:
> Le 21/07/2020 à 12:58, Bald Eagle a écrit :
> > I'm also curious as to why I got I got a core dump with no clipping, and no core
> > dump with half-clipping, if the domain input was the underlying issue.
Can you test this in POV-Ray and HGpovray38 to see if you get an error?
> > And I'm not even sure that the domain was out range now that we're back into
> > this again.
> > (I mean, can y ever exceed the vector length to give a quotient exceeding
> > unity?)
I did a quick spreadsheet calculation. Aside from some numerical/binary
representation/rounding it shouldn't.
>... there is a
> preference for the haversine formula instead of basic acos.
Nice. That was an interesting read - thanks!
> For your computation of latitude, you can use the complemented angle and
> asin instead, then complement the result, using the sign of y as final
> update.
>
> The loss of precision near 0 is far "better" than the loss of precision
> near 1, due to representation of floating point numbers.
>
> #declare Latitude = pi/2 - asin( sqrt( x*x+z*z)/sqrt(x*x+y*y+z*z) );
> #if (y<0)
> #declare Latitude = -1 * Latitude;
> #end
I dabbled with all of that.
It was "wrong" at first - since sin is opposite over hypotenuse, and y would be
the cathetus opposite the angle, it should be y/vlength instead of sqrt(
x*x+z*z)/vlength ... yes?
Which is kinda just what I had before, only using asin with a 90-deg phase
shift.
And I got the exact same result.
Which was disappointing at first, but which I recognized held promise.
So, after coffee, shower, and kicking back for a bit (it was NOT a nap...) I
realized that if, perhaps, it wasn't the math - then it had to be what the math
was mapping.
[TdG will back me up on the merits of considering these things behind closed
eyes.]
If the image was getting mapped correctly, but there were extra pixels in the
image... And sure enough, comparing the elevation map to a different image map
showed that there is indeed a strip of pixels where there ought be none.
Damn it.
Stupid assumptions...
"We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time...."
Thanks for spinning me around in this circle one more time, Jerome. :)
Now maybe I can make some actual meaningful progress...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 22/07/2020 om 02:24 schreef Bald Eagle:
[snip]
> Now maybe I can make some actual meaningful progress...
>
As you said, just close your eyes... ;-)
When I do, I see that hole in Antarctica you showed us, to be the lost
harbour of lost Lemuria. They just wait (with the help of climate
change) for the ice to disappear and conquer the world again.
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> As you said, just close your eyes... ;-)
.... and tap my shoes together...
> When I do, I see that hole in Antarctica you showed us, to be the lost
> harbour of lost Lemuria. They just wait (with the help of climate
> change) for the ice to disappear and conquer the world again.
Don't be ridiculous. It's obviously the Antarctic Ice Wall that guards the
secret entrance to the interior of the Hollow Earth - where all the spaceships
fly out of. org> wrote:
> As you said, just close your eyes... ;-)
.... and tap my shoes together...
> When I do, I see that hole in Antarctica you showed us, to be the lost
> harbour of lost Lemuria. They just wait (with the help of climate
> change) for the ice to disappear and conquer the world again.
Don't be ridiculous. It's obviously the Antarctic Ice Wall that guards the
secret entrance to the interior of the Hollow Earth - where all the spaceships
fly out of.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 22/07/2020 om 22:45 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
>> As you said, just close your eyes... ;-)
>
> .... and tap my shoes together...
>
>> When I do, I see that hole in Antarctica you showed us, to be the lost
>> harbour of lost Lemuria. They just wait (with the help of climate
>> change) for the ice to disappear and conquer the world again.
>
> Don't be ridiculous. It's obviously the Antarctic Ice Wall that guards the
> secret entrance to the interior of the Hollow Earth - where all the spaceships
> fly out of.
>
>
I had understood that Lemuria guarded /that/ entrance. Probably fake
news casually dropped by the usual suspects... :-)
--
Thomas org> wrote:
>
>> As you said, just close your eyes... ;-)
>
> .... and tap my shoes together...
>
>> When I do, I see that hole in Antarctica you showed us, to be the lost
>> harbour of lost Lemuria. They just wait (with the help of climate
>> change) for the ice to disappear and conquer the world again.
>
> Don't be ridiculous. It's obviously the Antarctic Ice Wall that guards the
> secret entrance to the interior of the Hollow Earth - where all the spaceships
> fly out of.
>
>
I had understood that Lemuria guarded /that/ entrance. Probably fake
news casually dropped by the usual suspects... :-)
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> I had understood that Lemuria guarded /that/ entrance. Probably fake
> news casually dropped by the usual suspects... :-)
Aye, Skull and bones, the Masons, the Illuminati, the Knights Templar, the
Knight of Malta, the Smithsonian, the Jesuits, the City of London, the Vatican,
the Illuminati... But we're not believing their transparent attempts at
misinformation and misdirection now, are we?
https://allthatsinteresting.com/lemuria-continent org> wrote:
> I had understood that Lemuria guarded /that/ entrance. Probably fake
> news casually dropped by the usual suspects... :-)
Aye, Skull and bones, the Masons, the Illuminati, the Knights Templar, the
Knight of Malta, the Smithsonian, the Jesuits, the City of London, the Vatican,
the Illuminati... But we're not believing their transparent attempts at
misinformation and misdirection now, are we?
https://allthatsinteresting.com/lemuria-continent
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 23/07/2020 om 12:43 schreef Bald Eagle:
> Thomas de Groot <tho### [at] degroot org> wrote:
>
>> I had understood that Lemuria guarded /that/ entrance. Probably fake
>> news casually dropped by the usual suspects... :-)
>
> Aye, Skull and bones, the Masons, the Illuminati, the Knights Templar, the
> Knight of Malta, the Smithsonian, the Jesuits, the City of London, the Vatican,
> the Illuminati... But we're not believing their transparent attempts at
> misinformation and misdirection now, are we?
>
> https://allthatsinteresting.com/lemuria-continent
>
>
>
LOL! Thanks for this. Very... illuminating. :-)
--
Thomas org> wrote:
>
>> I had understood that Lemuria guarded /that/ entrance. Probably fake
>> news casually dropped by the usual suspects... :-)
>
> Aye, Skull and bones, the Masons, the Illuminati, the Knights Templar, the
> Knight of Malta, the Smithsonian, the Jesuits, the City of London, the Vatican,
> the Illuminati... But we're not believing their transparent attempts at
> misinformation and misdirection now, are we?
>
> https://allthatsinteresting.com/lemuria-continent
>
>
>
LOL! Thanks for this. Very... illuminating. :-)
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()