 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I stuck with it and disabused my mind of whatever was plaguing it.
Primarily, it was a problem caused by evaluating the latitude using the
cartesian coordinates of the full volume of the isosurface contained_by shape.
That threw everything out of the valid -1 to 1 input range for the acos
function.
Just for future reference:
#declare Length = function (X, Y, Z) {sqrt(pow(X,2)+pow(Y,2)+pow(Z,2))}
#declare Lat = function (X, Y, Z) {acos ( min(Y/Length(X, Y, Z), 1) )}
#declare Long = function (X, Y, Z) {atan2 (Z, X)}
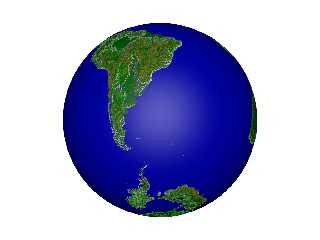
The displacement-map isosurface is on the left, and the bump_map from the same
image is on the right.
{whew}
Post a reply to this message
Attachments:
Download 'sphericalheightfieldtest.png' (211 KB)
Preview of image 'sphericalheightfieldtest.png'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Op 12/07/2020 om 03:55 schreef Bald Eagle:
> I stuck with it and disabused my mind of whatever was plaguing it.
>
> Primarily, it was a problem caused by evaluating the latitude using the
> cartesian coordinates of the full volume of the isosurface contained_by shape.
>
> That threw everything out of the valid -1 to 1 input range for the acos
> function.
>
> Just for future reference:
>
> #declare Length = function (X, Y, Z) {sqrt(pow(X,2)+pow(Y,2)+pow(Z,2))}
> #declare Lat = function (X, Y, Z) {acos ( min(Y/Length(X, Y, Z), 1) )}
> #declare Long = function (X, Y, Z) {atan2 (Z, X)}
>
>
> The displacement-map isosurface is on the left, and the bump_map from the same
> image is on the right.
>
> {whew}
>
Impressive. Good work. Depending on the ultimate use, one can opt for
the bump_map or the displacement_map. The displacement_map looks very
good: down to what level of detail?
--
Thomas
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Thomas de Groot <tho### [at] degroot org> wrote:
> Impressive. Good work. Depending on the ultimate use, one can opt for
> the bump_map or the displacement_map.
Yes - and believe it or not, the max gradient is less than 3, so it actually
renders surprisingly fast.
The real plan is to convert the elevation of what would normally be a
rectangular heighfield into the radius values for the spherical coordinate
system tiles.
At the very least for the corners and centers of the tiles - so that Everest and
Death valley aren't at the same elevation. ;)
But while I'm at it, why not do splines for edges, wireframe, and
bezier/triangle mesh.
> The displacement_map looks very
> good: down to what level of detail?
Let's see.
4320x2160 / [180x90] = 12x12 degrees lat/long x ~69 miles per degree
is about 828 miles square = 1332 meters per pixel
So, not terribly detailed, but it does look good - I'm only using 0.01 for a
multiplier of the elevation. So it can be made much more dramatic ;)
It's quite rough - like a non-smooth heightfield, which is perfect for
extracting the spline data, but for a displacement map used like this, a 3x3
convolution, Gaussian blur, or something like that could possibly make it look a
bit better.
As far as I know, this was the only way to get a "spherical heightfield".
If there are other ways to do this - I'd love to know! org> wrote:
> Impressive. Good work. Depending on the ultimate use, one can opt for
> the bump_map or the displacement_map.
Yes - and believe it or not, the max gradient is less than 3, so it actually
renders surprisingly fast.
The real plan is to convert the elevation of what would normally be a
rectangular heighfield into the radius values for the spherical coordinate
system tiles.
At the very least for the corners and centers of the tiles - so that Everest and
Death valley aren't at the same elevation. ;)
But while I'm at it, why not do splines for edges, wireframe, and
bezier/triangle mesh.
> The displacement_map looks very
> good: down to what level of detail?
Let's see.
4320x2160 / [180x90] = 12x12 degrees lat/long x ~69 miles per degree
is about 828 miles square = 1332 meters per pixel
So, not terribly detailed, but it does look good - I'm only using 0.01 for a
multiplier of the elevation. So it can be made much more dramatic ;)
It's quite rough - like a non-smooth heightfield, which is perfect for
extracting the spline data, but for a displacement map used like this, a 3x3
convolution, Gaussian blur, or something like that could possibly make it look a
bit better.
As far as I know, this was the only way to get a "spherical heightfield".
If there are other ways to do this - I'd love to know!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
>
> That threw everything out of the valid -1 to 1 input range for the acos
> function.
Nevertheless, the renderer should not dump core, regardless of user error. net> wrote:
>
> That threw everything out of the valid -1 to 1 input range for the acos
> function.
Nevertheless, the renderer should not dump core, regardless of user error.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 7/13/20 8:46 AM, Cousin Ricky wrote:
> "Bald Eagle" <cre### [at] netscape net> wrote:
>>
>> That threw everything out of the valid -1 to 1 input range for the acos
>> function.
>
> Nevertheless, the renderer should not dump core, regardless of user error.
>
In the FWIW catagory, it looks like a function POVFPU_Exception() was
mostly commented out in v3.7 and remains unchanged in v3.8. There are
some TODOs in the code for it. It's still called from many places in the
vm code, but...
Bill P. net> wrote:
>>
>> That threw everything out of the valid -1 to 1 input range for the acos
>> function.
>
> Nevertheless, the renderer should not dump core, regardless of user error.
>
In the FWIW catagory, it looks like a function POVFPU_Exception() was
mostly commented out in v3.7 and remains unchanged in v3.8. There are
some TODOs in the code for it. It's still called from many places in the
vm code, but...
Bill P.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
William F Pokorny <ano### [at] anonymous org> wrote:
> In the FWIW catagory, it looks like a function POVFPU_Exception() was
> mostly commented out in v3.7 and remains unchanged in v3.8. There are
> some TODOs in the code for it. It's still called from many places in the
> vm code, but...
>
> Bill P.
Well, it might have helped a bit to have an error message similar to "domain
error in atan2" or "divide by zero error", etc. before it shit the bed.
I'm still struggling with getting a good transition from the isosurface volume
coordinates to uv coordinates via the intermediate latitude/longitude values.
While what posted looks good superficially, I have a hole at the South pole, and
likely a similar issue at the North pole.
In my head, I should be able to take every <x,y,z> and convert it to a lat/long
pair (artificially constraining them to the proper domain) [maybe this is where
the error is], and then there should be a 1:1 [Abelian?] mapping between that
and the 0-1 domain of the x and y of the image map (the u,v).
Here's a plot of my uv's calculated from a cube from -3, +3 org> wrote:
> In the FWIW catagory, it looks like a function POVFPU_Exception() was
> mostly commented out in v3.7 and remains unchanged in v3.8. There are
> some TODOs in the code for it. It's still called from many places in the
> vm code, but...
>
> Bill P.
Well, it might have helped a bit to have an error message similar to "domain
error in atan2" or "divide by zero error", etc. before it shit the bed.
I'm still struggling with getting a good transition from the isosurface volume
coordinates to uv coordinates via the intermediate latitude/longitude values.
While what posted looks good superficially, I have a hole at the South pole, and
likely a similar issue at the North pole.
In my head, I should be able to take every <x,y,z> and convert it to a lat/long
pair (artificially constraining them to the proper domain) [maybe this is where
the error is], and then there should be a 1:1 [Abelian?] mapping between that
and the 0-1 domain of the x and y of the image map (the u,v).
Here's a plot of my uv's calculated from a cube from -3, +3
Post a reply to this message
Attachments:
Download 'sphericalheightfieldtest.png' (138 KB)
Preview of image 'sphericalheightfieldtest.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
I have a hole at the South pole, ...
Here's a view of the Antarctic hole:
[which sounds highly inappropriate, I know, but...] net> wrote:
I have a hole at the South pole, ...
Here's a view of the Antarctic hole:
[which sounds highly inappropriate, I know, but...]
Post a reply to this message
Attachments:
Download 'sphericalheightfieldtest_spole.png' (247 KB)
Preview of image 'sphericalheightfieldtest_spole.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 21/07/2020 à 03:20, Bald Eagle a écrit :
> "Bald Eagle" <cre### [at] netscape net> wrote:
> I have a hole at the South pole, ...
>
> Here's a view of the Antarctic hole:
>
> [which sounds highly inappropriate, I know, but...]
>
acos( min( y / length, 1) ) : the clipping is done for the north pole,
but not the south pole (-1)
what about "acos(max(min(y/length, 1),-1)) ? net> wrote:
> I have a hole at the South pole, ...
>
> Here's a view of the Antarctic hole:
>
> [which sounds highly inappropriate, I know, but...]
>
acos( min( y / length, 1) ) : the clipping is done for the north pole,
but not the south pole (-1)
what about "acos(max(min(y/length, 1),-1)) ?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron <jgr### [at] free fr> wrote:
> acos( min( y / length, 1) ) : the clipping is done for the north pole,
> but not the south pole (-1)
>
> what about "acos(max(min(y/length, 1),-1)) ?
Thanks Jerome, it was a good suggestion, but the hole is still there.
I'm also concerned that although I may happen upon a "solution" that looks nice
graphically, it will be numerically wrong. And that's because I'm going to be
using these calculations to "look up" the altitude on the rectangular elevation
map in order to construct planet tiles that are in the right position (as
closely as possible using this method and the data available).
I'm also curious as to why I got I got a core dump with no clipping, and no core
dump with half-clipping, if the domain input was the underlying issue. Because
without the min(), then I'd be running into the same problem that I was
imagining was happening, only with the opposite sign.
And I'm not even sure that the domain was out range now that we're back into
this again. (it's early, before coffee, and it's HOT)
(I mean, can y ever exceed the vector length to give a quotient exceeding
unity?)
I DO have my isosurface contained by a sphere instead of a box - maybe that has
something to do with it - I will check later this afternoon.
I really do have a knack for finding these little hidden problems... fr> wrote:
> acos( min( y / length, 1) ) : the clipping is done for the north pole,
> but not the south pole (-1)
>
> what about "acos(max(min(y/length, 1),-1)) ?
Thanks Jerome, it was a good suggestion, but the hole is still there.
I'm also concerned that although I may happen upon a "solution" that looks nice
graphically, it will be numerically wrong. And that's because I'm going to be
using these calculations to "look up" the altitude on the rectangular elevation
map in order to construct planet tiles that are in the right position (as
closely as possible using this method and the data available).
I'm also curious as to why I got I got a core dump with no clipping, and no core
dump with half-clipping, if the domain input was the underlying issue. Because
without the min(), then I'd be running into the same problem that I was
imagining was happening, only with the opposite sign.
And I'm not even sure that the domain was out range now that we're back into
this again. (it's early, before coffee, and it's HOT)
(I mean, can y ever exceed the vector length to give a quotient exceeding
unity?)
I DO have my isosurface contained by a sphere instead of a box - maybe that has
something to do with it - I will check later this afternoon.
I really do have a knack for finding these little hidden problems...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 21/07/2020 à 12:58, Bald Eagle a écrit :
> Le_Forgeron <jgr### [at] free fr> wrote:
>
>> acos( min( y / length, 1) ) : the clipping is done for the north pole,
>> but not the south pole (-1)
>>
>> what about "acos(max(min(y/length, 1),-1)) ?
>
> Thanks Jerome, it was a good suggestion, but the hole is still there.
>
> I'm also concerned that although I may happen upon a "solution" that looks nice
> graphically, it will be numerically wrong. And that's because I'm going to be
> using these calculations to "look up" the altitude on the rectangular elevation
> map in order to construct planet tiles that are in the right position (as
> closely as possible using this method and the data available).
>
> I'm also curious as to why I got I got a core dump with no clipping, and no core
> dump with half-clipping, if the domain input was the underlying issue. Because
> without the min(), then I'd be running into the same problem that I was
> imagining was happening, only with the opposite sign.
>
> And I'm not even sure that the domain was out range now that we're back into
> this again. (it's early, before coffee, and it's HOT)
> (I mean, can y ever exceed the vector length to give a quotient exceeding
> unity?)
> I DO have my isosurface contained by a sphere instead of a box - maybe that has
> something to do with it - I will check later this afternoon.
>
> I really do have a knack for finding these little hidden problems...
>
>
For playing with geodesique coordinates in another life, my
recommendation is that you should avoid acos formula, as for position
near the pole the precision is about 1-x²/2, which means you are getting
compression of detail at the pole so strong that you cannot tell apart
two poins that are 100 m aways.
When distance between two points is to be computed, there is a
preference for the haversine formula instead of basic acos.
For your computation of latitude, you can use the complemented angle and
asin instead, then complement the result, using the sign of y as final
update.
The loss of precision near 0 is far "better" than the loss of precision
near 1, due to representation of floating point numbers.
#declare Latitude = pi/2 - asin( sqrt( x*x+z*z)/sqrt(x*x+y*y+z*z) );
#if (y<0)
#declare Latitude = -1 * Latitude;
#end fr> wrote:
>
>> acos( min( y / length, 1) ) : the clipping is done for the north pole,
>> but not the south pole (-1)
>>
>> what about "acos(max(min(y/length, 1),-1)) ?
>
> Thanks Jerome, it was a good suggestion, but the hole is still there.
>
> I'm also concerned that although I may happen upon a "solution" that looks nice
> graphically, it will be numerically wrong. And that's because I'm going to be
> using these calculations to "look up" the altitude on the rectangular elevation
> map in order to construct planet tiles that are in the right position (as
> closely as possible using this method and the data available).
>
> I'm also curious as to why I got I got a core dump with no clipping, and no core
> dump with half-clipping, if the domain input was the underlying issue. Because
> without the min(), then I'd be running into the same problem that I was
> imagining was happening, only with the opposite sign.
>
> And I'm not even sure that the domain was out range now that we're back into
> this again. (it's early, before coffee, and it's HOT)
> (I mean, can y ever exceed the vector length to give a quotient exceeding
> unity?)
> I DO have my isosurface contained by a sphere instead of a box - maybe that has
> something to do with it - I will check later this afternoon.
>
> I really do have a knack for finding these little hidden problems...
>
>
For playing with geodesique coordinates in another life, my
recommendation is that you should avoid acos formula, as for position
near the pole the precision is about 1-x²/2, which means you are getting
compression of detail at the pole so strong that you cannot tell apart
two poins that are 100 m aways.
When distance between two points is to be computed, there is a
preference for the haversine formula instead of basic acos.
For your computation of latitude, you can use the complemented angle and
asin instead, then complement the result, using the sign of y as final
update.
The loss of precision near 0 is far "better" than the loss of precision
near 1, due to representation of floating point numbers.
#declare Latitude = pi/2 - asin( sqrt( x*x+z*z)/sqrt(x*x+y*y+z*z) );
#if (y<0)
#declare Latitude = -1 * Latitude;
#end
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()