 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I finally had enough time and energy to adapt some code for the Fourier
transform and implement it in SDL.
Great fun with arrays as always ;)
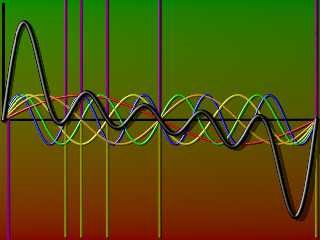
I made a simple data set by adding together some sine waves with different
frequencies and then applying the transform to that data.
Here's a quick sketch of the input data (black line), the component sine waves
(red, orange, yellow, green, and blue), the known frquencies (dark yellow
cylinders), and the FFT output (dark magenta cylinders)
Post a reply to this message
Attachments:
Download 'fft_test_2.png' (145 KB)
Preview of image 'fft_test_2.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
The preceding image clearly shows where the FFT picks out the individual
frequencies contributing to the summed waveform.
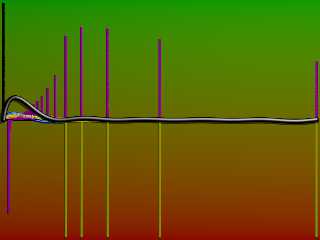
Since I used to do nuclear magnetic resonance spectroscopy, we collected raw RF
data from the sample probe, which was a sum of decaying amplitude sinusoidal
signals (like the positive side of a sinc graph) and performed FFT on that to
get the frequencies of the relaxing nuclei.
I modified the code a bit to show how the FFT picks out the primary frequencies
from the data when it's far less obvious where the full-wavelength nodes are.
I still need to automate the pre-FFT data array checking to make sure the data
set is an even power of 2 (or expand it to that, and fill with zeroes), figure
out to perform the inverse operation to get a sinusoid back, and then see if I
can find some code for a 2D FFT that's clear enough for me to follow.
It's been too long since I did any C, C#, C++, Perl, Javascript, etc. to really
be able to translate it to SDL in a timely manner.
I think it would be interesting to see how 1 and 2D Fourier transforms, coupled
with band-pass filtering would change the character of a heightfield use for a
landscape or water surface. "I'm thinking 1D would be something along the lines
of "anisotropic smoothing" and simulate wind-blown sand or waves... Perhaps
I'll see some day.
Post a reply to this message
Attachments:
Download 'fft_test_nmr.png' (56 KB)
Preview of image 'fft_test_nmr.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I think it would be interesting to see how 1 and 2D Fourier transforms, coupled
> with band-pass filtering would change the character of a heightfield use for a
> landscape or water surface. "I'm thinking 1D would be something along the lines
> of "anisotropic smoothing" and simulate wind-blown sand or waves... Perhaps
> I'll see some day.
Wow - VERY close, and uses POV-Ray to render the result! (claps)
http://geomorph.sourceforge.net/fourier/en/fourier_explorer_basics.html net> wrote:
> I think it would be interesting to see how 1 and 2D Fourier transforms, coupled
> with band-pass filtering would change the character of a heightfield use for a
> landscape or water surface. "I'm thinking 1D would be something along the lines
> of "anisotropic smoothing" and simulate wind-blown sand or waves... Perhaps
> I'll see some day.
Wow - VERY close, and uses POV-Ray to render the result! (claps)
http://geomorph.sourceforge.net/fourier/en/fourier_explorer_basics.html
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
This is really fascinating.
Although I don't have Linux on my machine (just Windows 7) and can't run
Geomorph, your post (and the Geomorph web page) are a really good introduction
to FFTs and how they apply to images. I've been thinking about this subject for
awhile (basically by reading just the Wikipedia page on FFTs!) and now the whole
idea behind FFT image manipulation is much clearer.
The Geomorph site's image examples look very similar to the effect that some of
Photoshop's image filters have on an image. Can I assume that Photoshop uses
FFTs for those filters?
Anyway, thanks for giving my brain a kick in the right direction ;-)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Kenneth" <kdw### [at] gmail com> wrote:
> This is really fascinating.
True, there's a lot more to it than I ever knew, but even the little I did know
suggested lots of interesting things to explore!
I don't have linux running on any of my machines - I suppose I ought to.
> The Geomorph site's image examples look very similar to the effect that some of
> Photoshop's image filters have on an image. Can I assume that Photoshop uses
> FFTs for those filters?
AFAIK, most of the bigger commercial packages use FT to process data for a lot
of the filters. I could be wrong, but reading and videos on FFT suggest
exactly that.
I'm thinking that 1D, 2D and 3D FFT would be useful for:
general smoothing, sharpening, edge-detection
Shape scanning and reconstruction (meshifying CSG objects and then converting to
isosurfaces)
Perhaps a heightfield be stored with only width/2 PLUS height/2 data points,
instead of full-width TIMES full-height data points?
Could the musical tones in an MP3 file be extracted and used to generate sheet
music in a POV-Ray scene?
generation of pigment patterns
modifying existing patterns by filtering
elimination of banding in gradients
comparing a spectrum before and after interacting with an object: any frequency
(vibration) absorption = harmonic frequencies of that object
feature and color analysis of images
Thanks for your interest :) com> wrote:
> This is really fascinating.
True, there's a lot more to it than I ever knew, but even the little I did know
suggested lots of interesting things to explore!
I don't have linux running on any of my machines - I suppose I ought to.
> The Geomorph site's image examples look very similar to the effect that some of
> Photoshop's image filters have on an image. Can I assume that Photoshop uses
> FFTs for those filters?
AFAIK, most of the bigger commercial packages use FT to process data for a lot
of the filters. I could be wrong, but reading and videos on FFT suggest
exactly that.
I'm thinking that 1D, 2D and 3D FFT would be useful for:
general smoothing, sharpening, edge-detection
Shape scanning and reconstruction (meshifying CSG objects and then converting to
isosurfaces)
Perhaps a heightfield be stored with only width/2 PLUS height/2 data points,
instead of full-width TIMES full-height data points?
Could the musical tones in an MP3 file be extracted and used to generate sheet
music in a POV-Ray scene?
generation of pigment patterns
modifying existing patterns by filtering
elimination of banding in gradients
comparing a spectrum before and after interacting with an object: any frequency
(vibration) absorption = harmonic frequencies of that object
feature and color analysis of images
Thanks for your interest :)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Kenneth" <kdw### [at] gmail com> wrote:
> Can I assume that Photoshop uses
> > FFTs for those filters?
"Digital image processing programs, such as Photoshop, use Fourier transforms
internally to perform certain image processing functions, such as Sharpen, Blur
and high and low band pass filters."
http://qsimaging.com/ccd_noise_create_ffts.html
Check out:
http://qsimaging.com/ccd_noise_interpret_ffts.html com> wrote:
> Can I assume that Photoshop uses
> > FFTs for those filters?
"Digital image processing programs, such as Photoshop, use Fourier transforms
internally to perform certain image processing functions, such as Sharpen, Blur
and high and low band pass filters."
http://qsimaging.com/ccd_noise_create_ffts.html
Check out:
http://qsimaging.com/ccd_noise_interpret_ffts.html
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> AFAIK, most of the bigger commercial packages use FT to process data for a lot
> of the filters. I could be wrong, but reading and videos on FFT suggest
> exactly that.
>
> I'm thinking that 1D, 2D and 3D FFT would be useful for:
>
> general smoothing, sharpening, edge-detection
If your filter is fixed, it's often faster to convert your
frequency-domain filter into a time-domain filter and optimise it (a
one-off cost), rather than doing an FFT and iFFT on the entire dataset.
> feature and color analysis of images
I came up with the idea (at work) of using FFT for measuring the speed
of jets of ink from a camera image. We implant a small vibration on the
fluid at a known temporal frequency (usually about 100 kHz, and we know
this frequency very accurately), then use FFT on the captured image to
get out the spatial frequency of the vibration (the jet diameter has a
slight sine wave on it). With these two bits of information you can
calculate the speed of the jet to a high accuracy even with quite bad
image quality.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
scott <sco### [at] scott com> wrote:
> > AFAIK, most of the bigger commercial packages use FT to process data for a lot
> > of the filters. I could be wrong, but reading and videos on FFT suggest
> > exactly that.
> >
> > I'm thinking that 1D, 2D and 3D FFT would be useful for:
> >
> > general smoothing, sharpening, edge-detection
>
> If your filter is fixed, it's often faster to convert your
> frequency-domain filter into a time-domain filter and optimise it (a
> one-off cost), rather than doing an FFT and iFFT on the entire dataset.
I'm still exploring the world of FT and what can be done with it.
It may take me some time to learn enough where what you just said will be
meaningful and I will understand _why_.
> I came up with the idea (at work) of using FFT for measuring the speed
> of jets of ink from a camera image. We implant a small vibration on the
> fluid at a known temporal frequency (usually about 100 kHz, and we know
> this frequency very accurately), then use FFT on the captured image to
> get out the spatial frequency of the vibration (the jet diameter has a
> slight sine wave on it). With these two bits of information you can
> calculate the speed of the jet to a high accuracy even with quite bad
> image quality.
That sounds pretty cool. Trying to visualize that and what the FT would look
like - if your jet is vertical in the image, then the result would be an
additional horizontal streak (due to the vibration) in the 2D FFT?
I'm just getting ready to run some test images through my code to see what the
output is, and if it makes sense intuitively, and is numerically correct.
I think I'd like to edit it so that "DC" is at the center of the 2D FFT so that
I can make more direct comparisons with most of what I see online.
What software package and FT library do you use?
Any assistance in understanding this all and creating some experiments and
demonstrations in SDL would be a huge help.
Thanks! com> wrote:
> > AFAIK, most of the bigger commercial packages use FT to process data for a lot
> > of the filters. I could be wrong, but reading and videos on FFT suggest
> > exactly that.
> >
> > I'm thinking that 1D, 2D and 3D FFT would be useful for:
> >
> > general smoothing, sharpening, edge-detection
>
> If your filter is fixed, it's often faster to convert your
> frequency-domain filter into a time-domain filter and optimise it (a
> one-off cost), rather than doing an FFT and iFFT on the entire dataset.
I'm still exploring the world of FT and what can be done with it.
It may take me some time to learn enough where what you just said will be
meaningful and I will understand _why_.
> I came up with the idea (at work) of using FFT for measuring the speed
> of jets of ink from a camera image. We implant a small vibration on the
> fluid at a known temporal frequency (usually about 100 kHz, and we know
> this frequency very accurately), then use FFT on the captured image to
> get out the spatial frequency of the vibration (the jet diameter has a
> slight sine wave on it). With these two bits of information you can
> calculate the speed of the jet to a high accuracy even with quite bad
> image quality.
That sounds pretty cool. Trying to visualize that and what the FT would look
like - if your jet is vertical in the image, then the result would be an
additional horizontal streak (due to the vibration) in the 2D FFT?
I'm just getting ready to run some test images through my code to see what the
output is, and if it makes sense intuitively, and is numerically correct.
I think I'd like to edit it so that "DC" is at the center of the 2D FFT so that
I can make more direct comparisons with most of what I see online.
What software package and FT library do you use?
Any assistance in understanding this all and creating some experiments and
demonstrations in SDL would be a huge help.
Thanks!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()