|
 |
"Cousin Ricky" <rickysttATyahooDOTcom> wrote:
> I get that message when I use the rgb keyword with a value that is already a 5
> component color. And it so happens that CHSV2RGB returns a 5 component color.
>
> Depending on the situation, I get rid of the message by using color or rgbft
> instead of rgb, or by omitting the keyword altogether.
Aha. Good to know.
Spent the last I dunno know how long chasing my tail trying to define an HSV
gradient as a function. I made a function pigment, and gave that an HSV
color_map - seems to work. Gonna try to alter the pigment function to something
more complex and see what that yields.
Color maps I guess are restricted to 256 entries, so doing the full 360 degrees
of HSV makes POV choke. So 0 to 360 step 2 it is.
Now what REALLY perplexes me is WHERE is my 4th harmonic?
I evaluated all of the equations in Excel just to see the values, and it
_should_ be there. But it's like the whole thing evaluates to zero.
1-Equation[3] gives me a sphere. 1000*Equation[3] gives nada.
//######################################################################
#version 3.7;
global_settings {assumed_gamma 1.0}
#include "colors.inc"
#include "textures.inc"
#include "shapes3.inc"
camera { location <7, 0, -15>
look_at <7, 0, 0>}
light_source {<40, 30, -20> White shadowless}
//light_source {<5.25, 5.25, 5.25> White shadowless}
background {Black}
#macro C_HSV2RGB(Color)
#local HSVFT = color Color;
#local H = (HSVFT.red);
#local S = (HSVFT.green);
#local V = (HSVFT.blue);
#local SatRGB = CH2RGB(H);
#local RGB = ( ((1-S)*<1,1,1> + S*SatRGB) * V );
<RGB.red,RGB.green,RGB.blue,(HSVFT.filter),(HSVFT.transmit)>
#end
#declare W = 3;
#for (N, 0, 5)
parametric {
#debug concat (str(N, 3, 2), "\n\n")
#ifndef (HH2) #local HH2 = function (S) {mod(sin(S/2)*360, 360)} #end
#ifndef (H2) #local H2 = function (S) {select (HH2(S), HH2(S)+360, HH2(S))}
#end // 0-120 120-240 240-360
#ifndef (R2) #local R2 = function (S) {select (mod(H2(S),240)-0.5,
(120-H2(S))/60, select (mod(H2(S),240)-1, (240-H2(S))/60, (H2(S)-240)/60 ) ) }
#end
#ifndef (G2) #local G2 = function (S) {select (mod(H2(S),240)-0.5, H2(S)/60,
select (mod(H2(S),240)-1, (240-H2(S))/60, 0 ) ) } #end
#ifndef (B2) #local B2 = function (S) {select (mod(H2(S),240)-0.5, 0,
select (mod(H2(S),240)-1, (H2(S)-120)/60, (360-H2(S))/60 ) ) } #end
#ifndef (Color)
#local Color = function {
spline {linear_spline
#for (CM, 0, 360)
CM/360, R2(CM), G2(CM), B2(CM)
#end // end for S
} // end spline
} // end function
#end
#ifndef (Q) #declare Q = function {(x*0)+1-y+(z*0)} #end
#declare Tex1 =
texture {
pigment {function {Q(x, y, z)}
color_map {
#for (CM, 0, 360, 2)
//[S/360, color <R(S), G(S), B(S)>]
[CM/360, color C_HSV2RGB(rgb <CM, 1, 1>)]
#end // end for S
} // end color map
} // end pigment
finish {specular 0.6}
scale 6
translate y*2.125
}
#declare Equation = array [6] {
function (u) {abs(1) },
function (u) {abs(cos(u)) },
function (u) {abs(3 * pow(cos(u),2) - 1) },
function (u) {abs(cos(u) * sin(u) * sin(v)) },
function (u) {abs(5 * pow(cos(u),3) - 3 * cos(u)) },
function (u) {abs( (5*pow(cos(u),2) - 1) * cos(v) * sin(u) ) },
}
#ifdef(E) #undef E #end
#declare E = Equation[N];
function { E(u)*sin(u)*cos(v) }, // x-axis
function { E(u)*sin(u)*sin(v) }, // y-axis
function { E(u)*cos(u) } // z-axis
<0, 0>, <pi, 2*pi> // <Umin, Vmin>, <Umax, VMax> (Theta, Phi = Altitude,
Azimuth)
contained_by { box { <-1,-1,-1>*W, <1,1,1>*W } }
// max_gradient 2
accuracy 0.0001
precompute 15 x,y,z
rotate x*90
scale 1
texture {Tex1}
translate x*3*N
}
#end // end for N
Post a reply to this message
Attachments:
Download 'sphericalharmonics_2.png' (18 KB)
Preview of image 'sphericalharmonics_2.png'
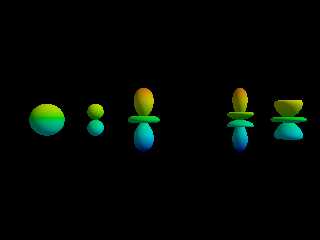
|
 |




![]()