|
 |
Here is the first of two technical images, the third can be ruled out. As I
first studied the discussion between Waggy and Tor Olav I misunderstood the
given explanations there. See
http://news.povray.org/povray.binaries.scene-files/thread/%3C4b2c7b3f%40news.povray.org%3E/
Tor Olav states there that his distance estimation function has to be improved
likely. And Waggy explained the idea behind this functions but I was to stupid
to comprehend this at first reading. In fact the original code of Tor Olav
rendered 31 minutes, but yielded a very smooth superset of the mandelbulb only.
There exists a lot of alternative formulas to generate mandelbulb like
structures. One of them is the use of the inbuild functions f_th and f_ph from
functions.inc, which return polar coordinates. Tor Olav uses this approach but
it is different from the mandelbulb first posted ever. I changed this in his
code to the original formula.
Despite the claim within the POV-docs that atan2(A,B) can handle the value B=0
("Returns appropriate value even if B is Zero") I get range violations in this
case and the render fails. So I had to use a work around. Simple, but may the
one or other can use it (see code below).
I still kept Tor Olav's wonderful technique to turn a recursive function into an
iterative one since recursive function calls are not supported by POV
officially. In most cases they work, but it is not guaranteed.
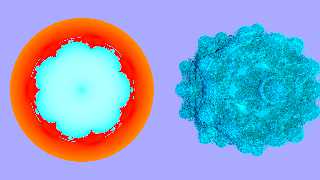
Here is the image using the distance estimation function proposed by Scott. I
still observe some problems (there seems to be some kind of bridges at the
right). To the left is an visualisation of the mandelbulb function as a pigment
function taken at the middle of the container object. It uses
color_map {
[0 Red ]
[0.5 Yellow ]
[1 Cyan ]
}
I rendered this to get a better understanding of the distance estimation
function (orange to red here). Note that Cyan indicates negative values close to
zero here (and not close to one).
Rendering time was 18 h 28 m. I think Scott's GPU approach will be a little bit
faster then POV.
Best regards,
Michael
/**************************************************************/
Code for the image:
/**************************************************************/
#version 3.7;
#include "colors.inc"
#include "functions.inc" // For f_r(), f_ph() and f_th()
#include "rad_def.inc"
global_settings { max_trace_level 256 radiosity {
Rad_Settings(Radiosity_OutdoorLQ,no,no) } }
#declare Atan2 = function(u,v){
select ( v,
select(u,atan2(u/v,1)-pi,atan2(u/v,1)+pi),// v<0
select(u,-pi/2,0,pi/2),// v=0
atan2(u/v,1)// v>0
)
}
#macro MandelBulbFunction(R_Pwr, R_BO, Ph_Pwr, Ph_Phase, Th_Pwr, Max_Iter)
#local ln_R_BO = ln(R_BO);
#local ln_R_Pwr = ln(R_Pwr);
#local J = Max_Iter - 1;
#local MB_Fns = array[Max_Iter][2]
#local I = Max_Iter;
#while (I > 0)
#local I = I - 1;
#local MB_Fns[I][1] =
function(x, y, z, _r, _rp, _ph, _th, _dr) {
#if (I = J)
0.5*ln(_r)*_r/_dr//0
#else
select(
_r - R_BO,
MB_Fns[I+1][0](
x,
y,
z,
/********************************************* TOK
x + _rp*cos(_ph)*cos(_th),
y + _rp*sin(_ph),
z + _rp*cos(_ph)*sin(_th),
*********************************************/
x + _rp*sin(_th)*cos(_ph),
y + _rp*sin(_th)*sin(_ph),
z + _rp*cos(_th),
_dr*_rp/_r*R_Pwr+1
),
// 1/(I - ln(ln(_r)/ln_R_BO)/ln_R_Pwr) // TOK
0.5*ln(_r)*_r/_dr
)
#end // if
}
#local MB_Fns[I][0] =
function(x, y, z, _ix, _iy, _iz,_dr) {
MB_Fns[I][1](
x,
y,
z,
f_r(_ix, _iy, _iz),
pow(f_r(_ix, _iy, _iz), R_Pwr),
/************************************************ TOK
Ph_Pwr*(f_ph(_ix, _iy, _iz) + Ph_Phase),
Th_Pwr*f_th(_ix, _iy, _iz),
*************************************************/
Ph_Pwr*Atan2(_iy,_ix),
Th_Pwr*Atan2(sqrt(_ix*_ix+_iy*_iy),_iz),
_dr
)
}
#end // while
function { MB_Fns[0][0](x, y, z, x, y, z, 1) }
#end // macro MandelBulbFunction
#declare CamPos=<0,0,-3>;
#declare Power_Radius = 8;// TOK: 8;
#declare Power_Phi = 8; // TOK: 8;
#declare Power_Theta = 8; // TOK: 8;
#declare Bailout_Radius = 2; // TOK: 3.0;
#declare Phase_Phi = 0; //TOK: pi/2;
#declare Max_Iterations = 64; // TOK: 5;
#declare Pigm=pigment {
MandelBulbFunction(
Power_Radius,
Bailout_Radius,
Power_Phi,
Phase_Phi,
Power_Theta,
Max_Iterations
)
color_map {
[0 Red ]
[0.5 Yellow ]
[1 Cyan ]
}
}
difference {
sphere { 0,1.2 }
box { <-2,-2,-2>,<2,2,0> }
pigment { Pigm }
translate <-1.3,0,0>
}
#declare MandelBulb=isosurface {
MandelBulbFunction(
Power_Radius,
Bailout_Radius,
Power_Phi,
Phase_Phi,
Power_Theta,
Max_Iterations
)
threshold 0
max_gradient 1000 // TOK: 20 // This value should probably be increased
accuracy 0.001
contained_by { sphere { <0, 0, 0>, 1.2 } }
texture {
pigment { color Cyan }
}
}
object { MandelBulb
translate <1.3,0,0>
}
light_source {
<2, 2, 2>*100
color White
}
light_source {
<2, -2, -2>*100
color White
}
light_source {
CamPos+0.25*x
color White
}
camera {
location CamPos
up y
right image_width/image_height*x
look_at <0, 0, 0>
}
background { color Gray40 + Blue }
Post a reply to this message
Attachments:
Download 'test_scott.png' (599 KB)
Preview of image 'test_scott.png'
|
 |




![]()