 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
#include "kolors.inc"
light_source { <10, 20, -30> rgb 1 }
camera {
perspective
location <3, 5, -15>
up y
right x*(image_width/image_height)
look_at 0
}
#default { pigment { White } }
#declare obj = sphere { 0, 0.25 }
union {
cylinder { -5*y, 5*y 0.0625 }
cylinder { -5*x, 5*x 0.0625 }
cylinder { -5*z, 5*z 0.0625 }
object { obj translate vrotate(<3,4,3>, <30, 60, 90>) }
translate -5.0*x
}
union {
cylinder { -5*y, 5*y 0.0625 }
cylinder { -5*x, 5*x 0.0625 }
cylinder { -5*z, 5*z 0.0625 }
object { obj translate <3,4,3> rotate <30, 60, 90> }
translate 5.0*x
}
Post a reply to this message
Attachments:
Download 'vrotate_test.png' (37 KB)
Preview of image 'vrotate_test.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
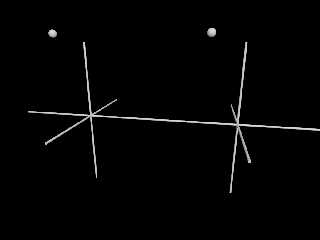
Er, that did nothing but confuse me. Especially the sphere.
The perspective camera didn't help.
#include "colors.inc"
camera { orthographic
location <-15, 0, -35>
//up y
//right x*(image_width/image_height)
look_at 0
}
light_source { <-15, 10, -30> rgb 1 }
background {color Blue*0.5}
// define variables
//#######################################################
#default { texture {pigment {White} finish {ambient 0.6}}}
#declare Translation_1 = 3;
#declare Translation_2 = 4;
#declare Translation_3 = -10;
#declare Diameter = 0.2;
#declare Length = 10;
#declare Coordinates_1 = vrotate (<Translation_1, Translation_2, Translation_3>,
<30, 0, 0>);
#declare Coordinates_2 = vrotate (<Translation_1, Translation_2, Translation_3>,
<30, 60, 0>);
#declare Coordinates_3 = vrotate (<Translation_1, Translation_2, Translation_3>,
<30, 60, 90>);
// define an obviously asymmetric object
//#######################################################
#declare obj = union{
cylinder { <0, 0, 0>, <0, 2, 0>, 0.125 }
sphere {<0, 2.125, 0>, 0.5}
cylinder { <0, 0, 0>, <2, 0, 0>, 0.125 }
box {<0, 0, 0>, <1, 1, 1> translate <1+0.5, -0.5, -0.5>}
cylinder { <0, 0, 0>, <0, 0, -2>, 0.125 }
cone {-z*2, 0.3, -z*2.25, 0 }
}
//#######################################################
/*
vrotate(A,B) Rotate A about origin by B.
Given the x,y,z coordinates of a point in space designated by the vector A
[<x1,y1,z1>],
rotate that point about the origin by an amount specified by the vector B
[<xr,yr,zr>].
Rotate it about the x-axis by an angle specified in degrees by the float value
B.x [xr].
Similarly B.y [yr] and B.z [zr] specify the amount to rotate in degrees about
the y-axis and z-axis.
The result [that vrotate returns] is a vector containing the new x,y,z
coordinates of the point [x2,y2,z2].
Description from POV-Ray Help, annotations in square brackets[ ].
*/
// EXAMPLE 1 - GREEN AXES
union {
cylinder { -Length*y, Length*y, Diameter texture {pigment {Green} finish
{ambient 0.6}} }
cylinder { -Length*x, Length*x, Diameter texture {pigment {Green} finish
{ambient 0.6}} }
cylinder { -Length*z, Length*z, Diameter texture {pigment {Green} finish
{ambient 0.6}} }
//################################################################################################
// THIS IS THE KEY CONCEPT - COMPARE TO AN ACTUAL ROTATION IN SECOND EXAMPLE
//################################################################################################
object { obj
translate vrotate(<Translation_1, Translation_2, Translation_3>, <30, 60,
90>)
texture {pigment {Yellow} finish {ambient 0.6}}
// TRANSLATE object at <x1, y1, z1> to where it would end up if rotated by
<30, 60, 90>
}
//^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
//################################################################################################
object {obj texture {pigment {Green} finish {ambient 0.6}} translate
<Translation_1, Translation_2, Translation_3>} // mark original position
object {obj texture {pigment {White transmit 0.5} finish {ambient 0.6}}
translate Coordinates_1}
torus {vlength(<0, Translation_2, Translation_3>), 0.2 rotate z*90 translate
x*Translation_1
texture {pigment {White transmit 0.7 } finish {ambient 0.4}} no_shadow}
object {obj texture {pigment {White transmit 0.5} finish {ambient 0.6}}
translate Coordinates_2}
torus {vlength (<Coordinates_1.x, 0, Coordinates_1.z>), 0.2 translate
y*Coordinates_1.y
texture {pigment {White transmit 0.7} finish {ambient 0.4}} no_shadow}
//sphere {<Translation_1, Translation_2, Translation_3>, 0.5 rotate x*30
rotate y*60 rotate z*90}
torus {vlength (<Coordinates_2.x, Coordinates_2.y, 0>), 0.2 rotate x*90
translate z*Coordinates_2.z
texture {pigment {White transmit 0.7} finish {ambient 0.4}} no_shadow}
cylinder { <Translation_1, Translation_2, Translation_3>, Coordinates_3,
Diameter
texture {pigment {Blue} finish {ambient 0.6}} }
//cone {x*(Translation_1-1), Diameter*3, x*Translation_1, 0 }
translate -15.0*x
}
//################################################################################################
// EXAMPLE 2
// RED AXES
union {
cylinder { -Length*y, Length*y Diameter texture {pigment {Red} finish
{ambient 0.6}}}
cylinder { -Length*x, Length*x Diameter texture {pigment {Red} finish
{ambient 0.6}}}
cylinder { -Length*z, Length*z Diameter texture {pigment {Red} finish
{ambient 0.6}}}
//################################################################################################
// HERE THE OBJECT IS ROTATED AROUND THE x, THEN y, THEN z AXES
//################################################################################################
object { obj
translate <Translation_1, Translation_2, Translation_3>
rotate <30, 60, 90> }
// NOTE THAT ALTHOUGH THE OBJECT WINDS UP AT THE SAME FINAL POSITION,
// ITS ORIENTATION HAS CHANGED DUE THE ROTATIONS
//################################################################################################
translate 10.0*x
texture {pigment {Yellow} finish {ambient 0.6}}
}
union{
object {obj translate <Translation_1, Translation_2, Translation_3>
texture {pigment {Green} finish {ambient 0.6}} } // mark original position
object {obj translate <Translation_1, Translation_2, Translation_3> rotate
x*30
texture {pigment {White transmit 0.5 } finish {ambient 0.6}} no_shadow}
torus {vlength(<0, Translation_2, Translation_3>), 0.2 rotate z*90 translate
x*Translation_1
texture {pigment {White transmit 0.7 } finish {ambient 0.4}} no_shadow}
object {obj translate <Translation_1, Translation_2, Translation_3> rotate
x*30 rotate y*60
texture {pigment {White transmit 0.5 } finish {ambient 0.6}} no_shadow}
torus {vlength (<Coordinates_1.x, 0, Coordinates_1.z>), 0.2 translate
y*Coordinates_1.y
texture {pigment {White transmit 0.7 } finish {ambient 0.4}} no_shadow}
//sphere {<Translation_1, Translation_2, Translation_3>, 0.5 rotate x*30
rotate y*60 rotate z*90}
torus {vlength (<Coordinates_2.x, Coordinates_2.y, 0>), 0.2 rotate x*90
translate z*Coordinates_2.z
texture {pigment {White transmit 0.7 } finish {ambient 0.4}} no_shadow}
cylinder { <Translation_1, Translation_2, Translation_3>, Coordinates_3,
Diameter
texture {pigment {Blue transmit 0.7} finish {ambient 0.6}} }
//cone {x*(Translation_1-1), Diameter*3, x*Translation_1, 0 }
translate x*10.0
}
Post a reply to this message
Attachments:
Download 'vrotate.png' (31 KB)
Preview of image 'vrotate.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> Er, that did nothing but confuse me. Especially the sphere.
> The perspective camera didn't help.
>
>
>
yeah... sorry about that. The documentation makes it clear that vrotate(A,B)
rotates a POINT (A) around the origin by a vector (B)
all well and good, but what it doesn't make clear -- expecting, I suppose that
it should be obvious -- is that when you do the same thing with an object, you
actually rotate the object's reference frame.
so what vrotate(A,B) does is apply a pre-translation rotation to the object, so
that when it is translated to A and then rotated by B, it is still in the same
orientation it had at the origin.
I hope this is clear.
e.g.
imagine you have an object at the origin, and you translate it to <3,0,0> then
rotate it about the origin by <0,0,90>
the object will now be at <0, 3, 0> but it will be lying on it's side.
in order to do what vrotate does, you need to first rotate the object by
<0, 0, -90>, then translate it by A and rotate it by B.
Regards,
A.D.B. net> wrote:
> Er, that did nothing but confuse me. Especially the sphere.
> The perspective camera didn't help.
>
>
>
yeah... sorry about that. The documentation makes it clear that vrotate(A,B)
rotates a POINT (A) around the origin by a vector (B)
all well and good, but what it doesn't make clear -- expecting, I suppose that
it should be obvious -- is that when you do the same thing with an object, you
actually rotate the object's reference frame.
so what vrotate(A,B) does is apply a pre-translation rotation to the object, so
that when it is translated to A and then rotated by B, it is still in the same
orientation it had at the origin.
I hope this is clear.
e.g.
imagine you have an object at the origin, and you translate it to <3,0,0> then
rotate it about the origin by <0,0,90>
the object will now be at <0, 3, 0> but it will be lying on it's side.
in order to do what vrotate does, you need to first rotate the object by
<0, 0, -90>, then translate it by A and rotate it by B.
Regards,
A.D.B.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
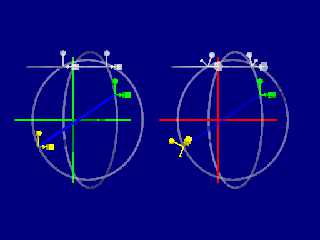
Of course, saying that vrotate applies a pre-translation rotation is not exactly
correct either.
The effect is much simpler: when you do
translate vrotate(A, B)
vrotate calculates where A will end up after being rotated around the origin by
B. It returns a vector which is then passed to translate. So the effect is as
if you had simply translated the object from the origin to the new point.
Sorry for any confusion.
Regards,
A.D.B.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> The effect is much simpler: when you do
>
> translate vrotate(A, B)
>
> vrotate calculates where A will end up after being rotated around the origin by
> B. It returns a vector which is then passed to translate. So the effect is as
> if you had simply translated the object from the origin to the new point.
Right. I made some annotations in my SDL code, and tried to show with the blue
line that that's exactly what it does.
I wouldn't say that the documentation is "clear", although it does say exactly
what vrotate() does. It just takes reading it 3 or 4 times to get it.
I hate that an <x,y,z> coordinate is referred to as a "vector".
To me, vector is a magnitude with a direction. I suppose if you're looking at
it from the perspective of moving _from_ the origin to that point, then yes, but
in my mind, it's JUST a point.
And the direction of a vector is actually important when using something like
trace(), which I learned when trying to understand THAT command...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Anthony D. Baye wrote:
> so what vrotate(A,B) does is apply a pre-translation rotation to the object, so
> that when it is translated to A and then rotated by B, it is still in the same
> orientation it had at the origin.
I think you are still a bit confused about this issue. Despite its name,
vrotate will NOT rotate an object at all. It is simply a vector function
that returns three value (the coordinates of point A rotated around the
axis defined by B). What you do with these 3 values is entirely up to
you, you can interpret them as color, point, direction or lottery
numbers. If you write
translate vrotate(A,B)
you interpret the resulting 3 values as a vector for translation
of the object. So the only transformation here is a translation and
therefore the orientation of the object remains unchanged.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 17.08.2013 02:34, schrieb Bald Eagle:
> I wouldn't say that the documentation is "clear", although it does say exactly
> what vrotate() does. It just takes reading it 3 or 4 times to get it.
> I hate that an <x,y,z> coordinate is referred to as a "vector".
>
> To me, vector is a magnitude with a direction. I suppose if you're looking at
> it from the perspective of moving _from_ the origin to that point, then yes, but
> in my mind, it's JUST a point.
You'd be surprised at the multitude of different things that
mathematicians call vectors ;-)
As a matter of fact, what you call "just a point" is called the
"location vector" of a point (while the other flavor of vector is called
a "direction vector").
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
ARrrrrrgh.
I would have thought that VangleD( <0, 0, 0>, <8, 8, 0>) would return 45
degrees.
Instead it returns 90.
VangleD( <8, 0, 0>, <8, 8, 0>) returns 45 degrees.
So, it's not the angle between the "vectors" that it returns, but the angle
formed by the Vector described by the two points, and an axis?
I will pursue defining the details of this function when I'm done working on my
current scene, but G's.... Talk about unintuitive.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 19.08.2013 03:23, schrieb Bald Eagle:
> ARrrrrrgh.
> I would have thought that VangleD( <0, 0, 0>, <8, 8, 0>) would return 45
> degrees.
> Instead it returns 90.
> VangleD( <8, 0, 0>, <8, 8, 0>) returns 45 degrees.
>
> So, it's not the angle between the "vectors" that it returns, but the angle
> formed by the Vector described by the two points, and an axis?
Well, I guess I'll resort to my standard answer again: "Um... no, not
really." :-)
Note that <0,0,0> has no direction, so the angle between it and any
other given vector is poorly defined. The function has to return
/something/, and it decides to return 90 because it's just as good or
bad as any other answer in that situation.
You can interpret the function in two ways:
(i) The function gives the angle between two direction vectors; to
understand what the angle between two vectors is, imagine both vectors
to be in the same plane (you can easily do this with any direction
vector because by definition a direction vector has no associated
location in space, just the direction and magnitude); the angle between
the two vectors is the rotation in that common plane that, when applied
to A, will reorient it to be collinear with vector B.
(ii) The function gives the angle between two location vectors; this is
equivalent to drawing two rays from the origin, one through each of the
points defined by the location vectors A and B, and - in the plane
defined by those two points and the origin - measuring the angle between
the two rays.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
> Note that <0,0,0> has no direction, so the angle between it and any
> other given vector is poorly defined. The function has to return
> /something/, and it decides to return 90 because it's just as good or
> bad as any other answer in that situation.
Except now we're being all loosey-goosey with the definition of "vector".
I would have understood or _assumed_ that like everything else, these would be
location vectors, not direction vectors.
Considering that VDist(A,B) gives me the distance between two location vectors,
I would be tempted to assume that if I wanted to draw a line between said points
(in the plane {z, 0}, I would draw a line from the origin to <VDist(A,B), 0, 0>,
and then rotate it by VAngleD(A,B), then translate it by <A.x, A.y, 0>
So yes, once again the directive does exactly what the documentation says it
does, but the documentation is not clear WHICH definition of "vector" is being
applied when interpreting the directive.
Now, granted, I do stoopid things and confuse myself all the time, but this was
a tricksy one, oh yes my preciousssss. Very tricksy indeed. Nasty little
directiveses. Not like End User it does. Hates us.
But it's ok, I'll be fine. The nice doctors said everything's gonna be "just
fine." :D
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()