 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
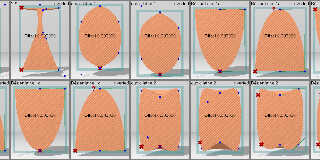
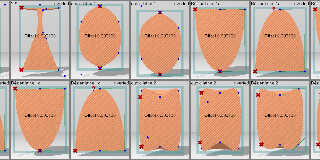
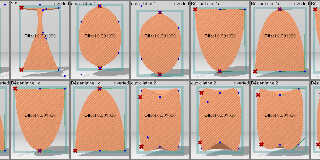
I want to compute the volume of arbitrary solids of revolution, and to
do this, I need to trace the objects. But with cubic and Bezier lathes,
trace() is hit or miss. These images show the results of trying to
trace the tops and bottoms of various shapes. All the shapes uses the
Sturm option.
- A '?' on the middle axis means the trace failed from above or
below. (There are no such failures in these illustrations.)
- A '?' near the top or bottom means the trace failed from the side.
- Two 'X's on the left side or convex apex mean all trace attempts were
successful.
- A single 'X' on the left side or convex apex means that a trace from
above or below went all the way through the shape, and hit the
other end!
- An 'X' on a concave end means that the trace missed from the side,
but hit the middle.
Image sor_extents.jpg traces the exact middle and the top and bottom of
the shape. Image sor_extents-4.jpg traces from offsets of 1E-4. Image
sor_extents-3.jpg traces from offsets of 1E-3.
As you can see, only with an accuracy of 0.001 can traces be guaranteed.
But this is with POV-Ray 3.7; results are different with other versions
of POV-Ray! I had to take it up to 0.005 to guarantee traces with 3.5.
Along with the images, I have attached the scene definition file and
#debug outputs from the 3.7 renders.
Post a reply to this message
Attachments:
Download 'sor_extents.jpg' (297 KB)
Download 'sor_extents-4.jpg' (298 KB)
Download 'sor_extents-3.jpg' (298 KB)
Download 'sor_extents.zip' (5 KB)
Preview of image 'sor_extents.jpg'
Preview of image 'sor_extents-4.jpg'
Preview of image 'sor_extents-3.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
[in v3.8.0 beta 1 Windows 10]
I ran your 14-frame animation over and over again, changing the 'Offset' from
0.0 by 0.0001 increments. On my system, the trace mistakes you mentioned finally
disappear at 0.0029. Strangely, there were instances where trace succeeded
completely, then the next increment would re-introduce them!
The use of sturm or no-sturm didn't seem to make a difference.
With Offset at 0.0, I also tried slightly rotating your 'form' objects (in all
three axes)-- like rotate 1 -- which again eliminated the trace mistakes. But
that's probably identical to using Offsets.
I would guess that there are mathematical inconsistencies (creating possible
holes in the shapes?) below a certain precision level...or that a strict x/y/z
tracing direction somehow interacts badly with the precision of the troublesome
shapes.
As a more general question, is it necessary to trace the objects strictly along
the x/y/z axes? In other words, would a random (OR ordered) series of trace
operations-- originating from a 'sphere' outside the object and all directed
toward <0,0,0> -- suit your purpose instead? Although, I suppose any indents in
the shapes would present a problem with that scheme.
Ideally, I would imagine that each trace direction needs to be aligned toward
the normal of the shape at each point-- but that would require a preliminary
trace operation to find the normal there!
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
hi,
Cousin Ricky <ric### [at] yahoo com> wrote:
> I want to compute the volume of arbitrary solids of revolution, and to
> do this, I need to trace the objects. ...
"Kenneth" <kdw### [at] gmail com> wrote:
> I want to compute the volume of arbitrary solids of revolution, and to
> do this, I need to trace the objects. ...
"Kenneth" <kdw### [at] gmail com> wrote:
> ...
> As a more general question, is it necessary to trace the objects strictly along
> the x/y/z axes?
I realise this thread is all about the lathe/trace interplay, but wonder why
'inside()' testing is not used/considered instead of 'trace()'.
regards, jr. com> wrote:
> ...
> As a more general question, is it necessary to trace the objects strictly along
> the x/y/z axes?
I realise this thread is all about the lathe/trace interplay, but wonder why
'inside()' testing is not used/considered instead of 'trace()'.
regards, jr.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 2022-04-27 13:31 9-40, Kenneth wrote:
>
> As a more general question, is it necessary to trace the objects strictly along
> the x/y/z axes? In other words, would a random (OR ordered) series of trace
> operations-- originating from a 'sphere' outside the object and all directed
> toward <0,0,0> -- suit your purpose instead?
I propose to use numerical integration, which requires slices
perpendicular to the y axis.
> Although, I suppose any indents in
> the shapes would present a problem with that scheme.
I intend to restrict the domain to objects that can be described with a
function in y; that is, with the same restrictions as the sor primitive.
(Which means the last 4 objects in each image would be rejected as
valid inputs.)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 2022-04-27 15:24 (-4), jr wrote:
>
> I realise this thread is all about the lathe/trace interplay, but wonder why
> 'inside()' testing is not used/considered instead of 'trace()'.
For computing volumes, inside tests would be more brute force than I
predict I will have patience for.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I have come up with an idea that might be a fix for the precision issue-- at
least for some of your lathe objects. I have not tested it thoroughly though; I
used only frame 3 of your animation for my test, the 'cubic lathe 1' object.
That shape uses your (first) array[6] for its construction points...
array[6]
{ <-3, 1>, <0, 2>, <3, 4.5>, <3, 9.5>, <0, 12>, <-3, 9.5>,
}
....so I made an 'intersection' of the resulting lathe object with a box:
....
#case (CUBIC)
intersection{
box{-6,<6,12,6>} // same y-height as in array
lathe { cubic_spline List (uv_Ctrls) rotate 0 }} #break
....
Even with Offset = 0, it looks like the trace at the top was successful. Perhaps
the coincident or overlapping y=12 values have somehow removed the tiny
precision error. HOW, I don't know. ;-)
Post a reply to this message
Attachments:
Download 'sor_extents_intersection_test.jpg' (38 KB)
Preview of image 'sor_extents_intersection_test.jpg'
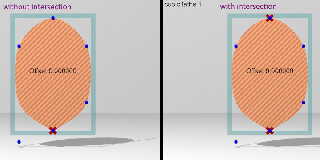
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 4/25/22 18:25, Cousin Ricky wrote:
> I want to compute the volume of arbitrary solids of revolution, and to
> do this, I need to trace the objects. But with cubic and Bezier lathes,
> trace() is hit or miss.
Thanks for the nice test case!
FWIW.
In a 'completely accurate' numerical result there are holes in the lathe
at the (top or bottom), OR, (top and bottom) depending upon whether
cubic or Bezier curves. When rays shot exactly vertical at the x,z
origin of the rotation about y. I cannot for certain recall which is
which at the moment.
Probably due the improved solvers; When I run your scene as shipped
(Offset 0) in my povr fork, I get vertical misses - but no side misses.
However, some of the side results are from the wrong end due there being
a hole on one end(a).
A recommendation would be to use the specified on curve points directly
when those align with the trace you'd otherwise do.
All said, trace, especially when the direction vector is 0 in one or
more its components, can be problematic depending upon the curve
specified and the ray being traced.
Bill P.
(a) - Where you have:
Ypt = trace (Form, adjStart, v_Dir, Norm);
and there is a hole the first vertical surface, but not the second, Ypt
gets set to the wrong location. The follow-on side trace is done at the
wrong (probably it's always a duplicate to the other 'side trace') y.
---
Aside: In povr, when I use a small offset in z, as in:
#local adjStart = (v_Start+<0,0,1e-6>) + Offset * x;
I no longer see misses for any vertical trace, but I introduce some side
misses. Those can be 'addressed' with a y specific offset:
#local Side = <v_Min.x - 1, Ypt.y + (f_sign(v_Dir.y) * 5e-3), 0>;
(The numerical y-view "hole(s)" at the ends has a related "trim" viewed
from the sides)
With the two changes above I get trace results with povr for all your
cases. However, trace is likely still unstable with respect to certain,
other lathe, curve specifications...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 2022-04-25 18:25 (-4), Cousin Ricky wrote:
> I want to compute the volume of arbitrary solids of revolution, ...
Meanwhile, my integral calculus needs a bit more work...
Post a reply to this message
Attachments:
Download 'sor_volume-res03.jpg' (19 KB)
Download 'sor_volume-res10.jpg' (26 KB)
Preview of image 'sor_volume-res03.jpg'

Preview of image 'sor_volume-res10.jpg'

|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()