|
 |
Hi(gh)!
I feel that it is time to think about the global planetary setting for
my "Port Whatmough" city project... so I started playing around with
pigment patterns (to be used as isosurfaces later on) to create
"physical maps" of that planet (i. e. Whatmough, named after the late
John Whatmough, founder of "Extrasolar Visions", www.extrasolar.net).
The planet should be roughly Earth-sized (probably somewhat smaller,
let's say 10,000 to 11,000 kms in diameter), with a slighter axial tilt
than Earth (~14 degrees) and also less land surface, concentrated mostly
in one main continent.
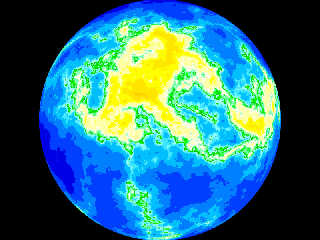
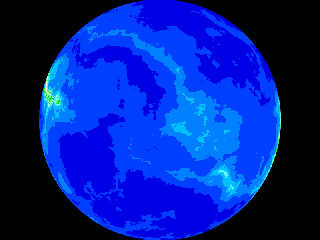
See attached images for what I've got using a special version of crackle...
...here's the code:
// beginning of code
camera
{
location <0, 0, -2.5>
look_at 0
angle 60
}
#declare P_Terrain_1=
pigment
{
crackle form <0, 0.3, 0>
color_map
{
[0 rgb <0, 0, 0.3>] // -10000 m
[0.1 rgb <0, 0, 0.3>]
[0.1 rgb <0, 0, 0.5>] // -8000 m
[0.2 rgb <0, 0, 0.5>]
[0.2 rgb <0, 0, 0.7>] // -6000 m
[0.3 rgb <0, 0, 0.7>]
[0.3 rgb <0, 0, 0.9>] // -4000 m
[0.4 rgb <0, 0, 0.9>]
[0.4 rgb <0, 0.25, 1>] // -2000 m
[0.45 rgb <0, 0.25, 1>]
[0.45 rgb <0, 0.5, 1>] // -1000 m
[0.475 rgb <0, 0.5, 1>]
[0.475 rgb <0, 0.75, 1>] // -500 m
[0.49 rgb <0, 0.75, 1>]
[0.49 rgb <0.25, 0.9, 1>] // -200 m
[0.495 rgb <0.25, 0.9, 1>]
[0.495 rgb <0.5, 1, 1>] // -100 m
[0.4975 rgb <0.5, 1, 1>]
[0.4975 rgb <0.7, 1, 1>] // -50 m
[0.5 rgb <0.7, 1, 1>] // 0 m, sea
[0.5 rgb <0, 0.8, 0>] // 0 m land
[0.5025 rgb <0, 0.8, 0>]
[0.5025 rgb <0, 1, 0>] // 50 m
[0.505 rgb <0, 1, 0>]
[0.505 rgb <0.5, 1, 0.7>] // 100 m
[0.51 rgb <0.5, 1, 0.7>]
[0.51 rgb <1, 1, 0.9>] // 200 m
[0.515 rgb <1, 1, 0.9>]
[0.515 rgb <1, 1, 0.65>] // 300 m
[0.525 rgb <1, 1, 0.65>]
[0.525 rgb <1, 1, 0>] // 500 m
[0.535 rgb <1, 1, 0>]
[0.535 rgb <1, 0.9, 0>] // 700 m
[0.55 rgb <1, 0.9, 0>]
[0.55 rgb <1, 0.8, 0>] // 1000 m
[0.575 rgb <1, 0.8, 0>]
[0.575 rgb <1, 0.7, 0>] // 1500 m
[0.6 rgb <1, 0.7, 0>]
[0.6 rgb <1, 0.6, 0>] // 2000 m
[0.625 rgb <1, 0.6, 0>]
[0.625 rgb <1, 0.5, 0>] // 2500 m
[0.65 rgb <1, 0.5, 0>]
[0.65 rgb <1, 0.4, 0>] // 3000 m
[0.7 rgb <1, 0.4, 0>]
[0.7 rgb <1, 0.2, 0>] // 4000 m
[0.75 rgb <1, 0.2, 0>]
[0.75 rgb <1, 0, 0>] // 5000 m
[0.8 rgb <1, 0, 0>]
[0.8 rgb 0.5] // 6000 m
[0.85 rgb 0.5]
[0.85 rgb 0.65] // 7000 m
[0.9 rgb 0.65]
[0.9 rgb 0.8] // 8000 m
[0.95 rgb 0.8]
[0.95 rgb 0.95] // 9000 m
[1 rgb 0.95] // 10000 m
}
translate <2, 0, 0>
turbulence 0.5
octaves 8
omega 0.6
lambda 2.07
poly_wave 0.53
}
sphere
{
0, 1
texture
{
pigment { P_Terrain_1 }
finish
{
ambient 1
diffuse 0
}
}
rotate y*0
}
// end of code
The problem is: I want to have wider lowlands (below 200 metres), but
also a few, but defined mountain ranges rising above the snow line
(above 4000 metres). With that crackle function I only get comparatively
narrow lowlands and gently sloping highlands which rarely rise higher
than 1000 metres.
What pigment/function of combination of functions would you recommend? I
tried f_ridged_mf, but as the color_map repeated itself, it proved
unsuitable.
The height distribution I need would resemble the graph of a cubic
function, with a "saddle" around 0 (0.5 in the color_map)... I in fact
tried several kinds of cubic functions (such as
pow(x,3)+pow(y,3)+pow(z,3)), but the results were utterly weird and of
no use for a physical map of a planet.
See you in Khyberspace!
Yadgar
Post a reply to this message
Attachments:
Download '2012-06-27 pigment test - whatmough, take 1.jpg' (180 KB)
Download '2012-06-27 pigment test - whatmough, take 2.jpg' (81 KB)
Preview of image '2012-06-27 pigment test - whatmough, take 1.jpg'
Preview of image '2012-06-27 pigment test - whatmough, take 2.jpg'
|
 |




![]()