 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
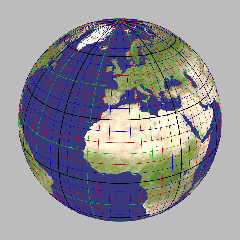
Using a mercator projection (100% spherical projection), but not as
usual (instead of a point on equator for center, using the south pole,
and forget about Greenwich meridian, off by 60°)
For once, groenland and australia seems approximatively right in
relative area.
Can you locate your home ?
Post a reply to this message
Attachments:
Download 'mercat2.jpg' (722 KB)
Download 'perspec.jpg' (319 KB)
Preview of image 'mercat2.jpg'

Preview of image 'perspec.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le_Forgeron wrote:
> Using a mercator projection (100% spherical projection), but not as
> usual (instead of a point on equator for center, using the south pole,
> and forget about Greenwich meridian, off by 60°)
I think this is a transverse Mercator projection (Lambert 1772)
for a specific choice of central meridian (the usual representation
seems to be shifted 25% with respect to yours, though, i.e. poles
at 25% and 75% and equator at center and border).
http://en.wikipedia.org/wiki/Transverse_Mercator_projection
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 19.12.2011 21:53, schrieb Le_Forgeron:
> Using a mercator projection (100% spherical projection), but not as
> usual (instead of a point on equator for center, using the south pole,
> and forget about Greenwich meridian, off by 60°)
FYI, the projection you used is not a transverse Mercator, but Cassini
(aka transverse equirectangular projection). Mercator would project your
"outer equator" into infinity, so it would not be visible on the map;
likewise, eastern Africa would not be that "squished", but rather just
out of proportion in size.
BTW, you seem to have some strange phenomenon in the waters of the Bahamas.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
clipka <ano### [at] anonymous org> wrote:
> BTW, you seem to have some strange phenomenon in the waters of the Bahamas.
That is merely the natural appearance of the crystal clear turquoise waters in
our part of the world. :-) org> wrote:
> BTW, you seem to have some strange phenomenon in the waters of the Bahamas.
That is merely the natural appearance of the crystal clear turquoise waters in
our part of the world. :-)
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 20/12/2011 01:42, clipka a écrit :
> FYI, the projection you used is not a transverse Mercator, but Cassini
> (aka transverse equirectangular projection). Mercator would project your
> "outer equator" into infinity,
HS! You're probably right. Mercator would use a cylinder and so far I'm
on a sphere. Bad me, very bad me.
Back to the drawing table and the equations... put the right labels on
the right bottles...
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
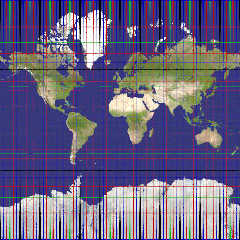
Le 20/12/2011 09:35, Le_Forgeron nous fit lire :
> Le 20/12/2011 01:42, clipka a écrit :
>> FYI, the projection you used is not a transverse Mercator, but Cassini
>> (aka transverse equirectangular projection). Mercator would project your
>> "outer equator" into infinity,
Yep, now that's Mercator, using a square map (and aspect ratio 1:1).
Post a reply to this message
Attachments:
Download 'mercat.jpg' (148 KB)
Preview of image 'mercat.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 21.12.2011 21:06, schrieb Le_Forgeron:
> Le 20/12/2011 09:35, Le_Forgeron nous fit lire :
>> Le 20/12/2011 01:42, clipka a écrit :
>>> FYI, the projection you used is not a transverse Mercator, but Cassini
>>> (aka transverse equirectangular projection). Mercator would project your
>>> "outer equator" into infinity,
>
> Yep, now that's Mercator, using a square map (and aspect ratio 1:1).
Ah, yes, Mercator: The only map projection that's absolutely uselsess
except for the single purpose of Navigating from A to B using nothing
but a compass. (And from what I know it's also the only projection that
does fit this purpose.)
You seem to have placed blue caps at the poles; is it a mere coincidence
that they're just the right size to show up on the northern and southern
edges of the map?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Le 22/12/2011 07:06, clipka a écrit :
> You seem to have placed blue caps at the poles; is it a mere coincidence
> that they're just the right size to show up on the northern and southern
> edges of the map?
I put torus all over the spherical earth (not yet ready to scale it for
the delta of 23 km over 6000+ km), same scene as for the original post
of this threads, just different camera. They are spaced 5° apart, with a
colour coding (black is 0, 30, ..; multiple of 15 are green; multiple of
10 are red, and other are blue). So, yes, it's a mere coincidence that
the blue ones get in front at the edge.
In fact, the black torus are a bit bigger, so extending further the map
(with a 3:4 ratio for instance) would get a blacker edge. But there is
no real interest of such picture (at least with the torus), isn't there ?
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()