 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I did some experiments to express the SuperFunction from
Dave Vogt's post with a single isosurface. It seems to work
fine.
Dave's original links:
[1] http://www.heise.de/newsticker/meldung/45863
[2] http://www.genicap.com/
[3] http://astronomy.swin.edu.au/~pbourke/povray/supershape/
The PovRay code as a Macro:
......................................
#macro Super_Function_3D (m1, a1, b1, n11, n21, n31, m2, a2, b2, n12, n22, n32 )
isosurface {
function {
pow( pow(abs(cos(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/a2),n22) +
pow(abs(sin(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/b2),n32)
,1/n12) *
pow( pow(abs(cos(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/a1),n21) +
pow(abs(sin(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/b1),n31)
,1/n11) *
sqrt (x*x+y*y+z*z)
- 1
}
max_gradient 20
contained_by { box { <-2,-2,-2>,<2,2,2> } }
}
#end
.........................................
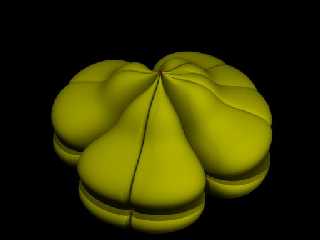
And a test image with the following parameters taken from an example on link [3]:
{ Super_Function_3D ( 7, 1, 1, 20.45, -0.33, -3.54, 6, 1, 1 ,-0.96, 4.46, 0.52 ) }
Regards, Hans
Post a reply to this message
Attachments:
Download 'superfunction_isosurface.jpg' (14 KB)
Preview of image 'superfunction_isosurface.jpg'
|
 |
|  |
|  |
|
 |
From: Tor Olav Kristensen
Subject: Re: Super Shapes with isosurface
Date: 22 Mar 2004 20:46:50
Message: <405f970a@news.povray.org>
|
|
 |
|  |
|  |
|
 |
Hans de Vries wrote:
...
> function {
> pow(
> pow(abs(cos(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/a2),n22) +
>
> pow(abs(sin(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/b2),n32)
> ,1/n12) *
>
> pow(
> pow(abs(cos(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/a1),n21) +
>
> pow(abs(sin(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/b1),n31)
> ,1/n11) *
>
> sqrt (x*x+y*y+z*z)
> - 1
> }
...
You can _try_ to increase the rendering speed, by replacing
'sqrt(x*x+y*y+z*z)' with 'f_r(x, y, z)' and 'sqrt(x*x+y*y)'
with 'f_r(x, y, 0)'.
Also you should have a look at the internal functions;
'f_th()' and 'f_ph()'.
http://www.povray.org/documentation/view/244/
Because it seems like these may enable you to simplify some
of your inverse trigonometric expressions.
E.g. this one: 'acos(y/sqrt(x*x+y*y))*abs(y)/y'
In order to use these functions, you must first include the
'functions.inc' file.
P.S.: antan2() is also useful.
--
Tor Olav
http://subcube.com
http://subcube.net
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
The simplest version for the time being below. It speeds things up with circa 25%
The trick is to get the right ranges for theta (-pi..+pi) and phi (-pi/2..+pi/2)
and avoiding divides by zero.
#macro Super_Function_3D (m1, a1, b1, n11, n21, n31, m2, a2, b2, n12, n22, n32 )
isosurface {
function {
pow( pow(abs(cos(0.25*m2*(f_ph(x,z,y)-pi/2))/a2),n22) +
pow(abs(sin(0.25*m2*(f_ph(x,z,y)-pi/2))/b2),n32)
,1/n12) *
pow( pow(abs(cos(0.25*m1*atan2(x,y))/a1),n21) +
pow(abs(sin(0.25*m1*atan2(x,y))/b1),n31)
,1/n11) *
f_r(x,y,z)
- 1
}
max_gradient 20
contained_by { box { <-2,-2,-2>,<2,2,2> } }
}
#end
Regards, Hans
Tor Olav Kristensen wrote:
> Hans de Vries wrote:
> ...
>
>> function {
>> pow(
>> pow(abs(cos(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/a2),n22) +
>>
>> pow(abs(sin(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/b2),n32)
>> ,1/n12) *
>>
>> pow(
>> pow(abs(cos(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/a1),n21) +
>>
>> pow(abs(sin(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/b1),n31)
>> ,1/n11) *
>>
>> sqrt (x*x+y*y+z*z)
>> - 1
>> }
>
> ...
>
> You can _try_ to increase the rendering speed, by replacing
> 'sqrt(x*x+y*y+z*z)' with 'f_r(x, y, z)' and 'sqrt(x*x+y*y)'
> with 'f_r(x, y, 0)'.
>
> Also you should have a look at the internal functions;
> 'f_th()' and 'f_ph()'.
>
> http://www.povray.org/documentation/view/244/
>
> Because it seems like these may enable you to simplify some
> of your inverse trigonometric expressions.
>
> E.g. this one: 'acos(y/sqrt(x*x+y*y))*abs(y)/y'
>
> In order to use these functions, you must first include the
> 'functions.inc' file.
>
> P.S.: antan2() is also useful.
>
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hans de Vries wrote:
>
> The simplest version for the time being below. It speeds things up with
> circa 25%
> The trick is to get the right ranges for theta (-pi..+pi) and phi
> (-pi/2..+pi/2)
> and avoiding divides by zero.
Often it will also help to "predeclare" constants so that they
don't have to be evaluated over and over again at rendertime.
E.g.:
#macro Super_Function_3D()
#local HalfPi = pi/2;
#local mm1 = 0.25*m1;
#local mm2 = 0.25*m2;
#local inn11 = 1/n11;
#local inn12 = 1/n12;
isosurface {
function {
pow(
pow(abs(cos(mm2*(f_ph(x, z, y) - HalfPi))/a2), n22) +
pow(abs(sin(mm2*(f_ph(x, z, y) - HalfPi))/b2), n32),
inn12
) *
pow(
pow(abs(cos(mm1*atan2(x, y))/a1), n21) +
pow(abs(sin(mm1*atan2(x, y))/b1), n31),
inn11
) *
f_r(x,y,z)
- 1
}
max_gradient 20
contained_by { box { <-2,-2,-2>,<2,2,2> } }
}
> #macro Super_Function_3D (m1, a1, b1, n11, n21, n31, m2, a2, b2, n12,
> n22, n32 )
>
> isosurface {
> function {
> pow( pow(abs(cos(0.25*m2*(f_ph(x,z,y)-pi/2))/a2),n22) +
> pow(abs(sin(0.25*m2*(f_ph(x,z,y)-pi/2))/b2),n32)
> ,1/n12) *
>
> pow( pow(abs(cos(0.25*m1*atan2(x,y))/a1),n21) +
> pow(abs(sin(0.25*m1*atan2(x,y))/b1),n31)
> ,1/n11) *
>
> f_r(x,y,z)
> - 1
> }
> max_gradient 20
> contained_by { box { <-2,-2,-2>,<2,2,2> } }
> }
>
> #end
>
> Regards, Hans
>
> Tor Olav Kristensen wrote:
>
>> Hans de Vries wrote:
>> ...
>>
>>> function {
>>> pow(
>>> pow(abs(cos(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/a2),n22) +
>>>
>>> pow(abs(sin(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/b2),n32)
>>> ,1/n12) *
>>>
>>> pow(
>>> pow(abs(cos(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/a1),n21) +
>>>
>>> pow(abs(sin(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/b1),n31)
>>> ,1/n11) *
>>>
>>> sqrt (x*x+y*y+z*z)
>>> - 1
>>> }
--
Tor Olav
http://subcube.com
http://subcube.net
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I enjoyed the images at your photo side.
http://subcube.com
Some very nice isosurfaces over there :^)
Regards, Hans
Tor Olav Kristensen wrote:
> Hans de Vries wrote:
>
>>
>> The simplest version for the time being below. It speeds things up
>> with circa 25%
>> The trick is to get the right ranges for theta (-pi..+pi) and phi
>> (-pi/2..+pi/2)
>> and avoiding divides by zero.
>
>
> Often it will also help to "predeclare" constants so that they
> don't have to be evaluated over and over again at rendertime.
>
> E.g.:
>
> #macro Super_Function_3D()
>
> #local HalfPi = pi/2;
> #local mm1 = 0.25*m1;
> #local mm2 = 0.25*m2;
> #local inn11 = 1/n11;
> #local inn12 = 1/n12;
>
> isosurface {
> function {
> pow(
> pow(abs(cos(mm2*(f_ph(x, z, y) - HalfPi))/a2), n22) +
> pow(abs(sin(mm2*(f_ph(x, z, y) - HalfPi))/b2), n32),
> inn12
> ) *
> pow(
> pow(abs(cos(mm1*atan2(x, y))/a1), n21) +
> pow(abs(sin(mm1*atan2(x, y))/b1), n31),
> inn11
> ) *
> f_r(x,y,z)
> - 1
> }
> max_gradient 20
> contained_by { box { <-2,-2,-2>,<2,2,2> } }
> }
>
>
>> #macro Super_Function_3D (m1, a1, b1, n11, n21, n31, m2, a2, b2, n12,
>> n22, n32 )
>>
>> isosurface {
>> function {
>> pow( pow(abs(cos(0.25*m2*(f_ph(x,z,y)-pi/2))/a2),n22) +
>> pow(abs(sin(0.25*m2*(f_ph(x,z,y)-pi/2))/b2),n32)
>> ,1/n12) *
>>
>> pow( pow(abs(cos(0.25*m1*atan2(x,y))/a1),n21) +
>> pow(abs(sin(0.25*m1*atan2(x,y))/b1),n31)
>> ,1/n11) *
>>
>> f_r(x,y,z)
>> - 1
>> }
>> max_gradient 20
>> contained_by { box { <-2,-2,-2>,<2,2,2> } }
>> }
>>
>> #end
>>
>> Regards, Hans
>>
>> Tor Olav Kristensen wrote:
>>
>>> Hans de Vries wrote:
>>> ...
>>>
>>>> function {
>>>> pow(
>>>> pow(abs(cos(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/a2),n22) +
>>>>
>>>> pow(abs(sin(0.25*m2*asin(z/sqrt(x*x+y*y+z*z)))/b2),n32)
>>>> ,1/n12) *
>>>>
>>>> pow(
>>>> pow(abs(cos(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/a1),n21) +
>>>>
>>>> pow(abs(sin(0.25*m1*acos(y/sqrt(x*x+y*y))*abs(y)/y)/b1),n31)
>>>> ,1/n11) *
>>>>
>>>> sqrt (x*x+y*y+z*z)
>>>> - 1
>>>> }
>
>
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hans de Vries wrote:
> I enjoyed the images at your photo side.
>
> http://subcube.com
>
> Some very nice isosurfaces over there :^)
Thank you Hans !
If you are interested in further "tricks" to make isosurfaces
render faster in POV-Ray you can find some in this thread:
http://news.povray.org/povray.text.scene-files/thread/%3Cweb.3fbbe555cd7b5c811235fd70%40news.povray.org%3E/
(Alex Kluchikov's thread "My favourite isosurface" posted
19. Nov. 2003 to povray.text.scene-files)
Or more specific:
http://tinyurl.com/2fbt5
http://tinyurl.com/yu42p
http://tinyurl.com/24dqh
http://tinyurl.com/3f642
--
Tor Olav
http://subcube.com
http://subcube.net
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()