|
 |
Hello,
This is a technical question and suited for povray.general or
advanced-users, but because I had to post the image here, it's easier for
everyone that I ask here too:
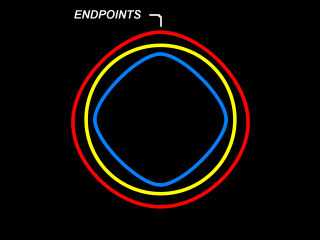
You see a red cubic spline, created with Pov3.5.
You see a yellow circle.
You see a blue cubic spline, created with Colefax's spline generator.
Until recently I thought the red spline would look like the yellow circle..
I fortunately got smarter and realize there are many kinds of cubic
splines.. But I wonder what kind Pov3.5 uses?
I once thought cubic splines merely took the position of 3 control points to
determine slope: the point before, now, and after.. This can't be true.. The
red spline is mostly different from the yellow circle at the endpoints, so I
conclude that cubic splines uses the *slope* of the points before and after,
and not only their position.. The slope - or is it called nodes? - of the
points beyond the endpoints have not been defined, only their position has..
(Here's the code, if you're interested)
#declare The_Spline=spline { cubic_spline
-0.25,<-1,0,0>
0.000000001,< 0,1,0> // due to Pov3.5 beta problem
0.25,< 1,0,0>
0.50,<0,-1,0>
0.75,<-1,0,0>
1.00,< 0,1,0>
1.25,< 1,0,0> }
I compared Chris Colefax's excellent spline generator to all this.. This has
control of tension, continuity and bias, and although I used the default
cubic spline, TCB is still used.. I also used the "loop" feature which might
cause the endpoints to look like the rest of points.. I have read about it
but, are cubic splines in Pov3.5 the same as Colefax's except the TCB
implementation?
Hugo
Post a reply to this message
Attachments:
Download 'Circular splines.JPG' (16 KB)
Preview of image 'Circular splines.JPG'
|
 |
|
 |
I don't remember Chris Colefax's include file and don't know sources for POV 3.5
but it is logical for me if there are two things within 3.5 with the same name
then they are similiar. So check cubic_spline desciption within Lathe chapter
(6.5.1.7) - perhaps there could be some answers to your question.
ABX
--
#declare _=function(a,b,x){((a^2)+(b^2))^.5-x}#default {pigment{color rgb 1}}
union{plane{y,-3}plane{-x,-3}finish{reflection 1 ambient 0}}isosurface{ //ABX
function{_(x-2,y,1)|_((x+y)*.7,z,.1)|_((x+y+2)*.7,z,.1)|_(x/2+y*.8+1.5,z,.1)}
contained_by{box{<0,-3,-.1>,<3,0,.1>}}translate z*15finish{ambient 1}}//POV35
Post a reply to this message
|
 |




![]()