 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
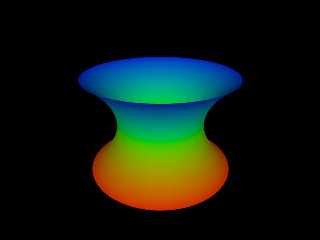
OK, I am sold on iso-surfaces. A long time project of mine has been to
create a catenoid (minimal surface object created by rotating a catenary
(shape a hanging rope makes)).
Functions are fantastic. Here it is:
Post a reply to this message
Attachments:
Download 'catenoid.jpg' (11 KB)
Preview of image 'catenoid.jpg'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Your ropes hang that way?
Duncan Adamson wrote:
> OK, I am sold on iso-surfaces. A long time project of mine has been to
> create a catenoid (minimal surface object created by rotating a catenary
> (shape a hanging rope makes)).
>
> Functions are fantastic. Here it is:
>
>
>
>
>
> catenoid.jpg
>
> Content-Type:
>
> image/jpeg
> Content-Encoding:
>
> x-uuencode
>
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Hang a rope from two points <0,1,0> and <1,1,0>
The shape it makes is a caterary
Rotate this shape around the x axis to get a catenoid (formula radius =
(1/a)cosh(ax))
My catenoid has been rotated to stand on its end.
Duncan
"Is" <mee### [at] yahoo com> wrote in message news:3BB### [at] yahoo com> wrote in message news:3BB### [at] yahoo com...
> Your ropes hang that way?
>
>
> Duncan Adamson wrote:
> > OK, I am sold on iso-surfaces. A long time project of mine has been to
> > create a catenoid (minimal surface object created by rotating a catenary
> > (shape a hanging rope makes)).
> >
> > Functions are fantastic. Here it is:
> >
> >
> >
> >
> >
> > catenoid.jpg
> >
> > Content-Type:
> >
> > image/jpeg
> > Content-Encoding:
> >
> > x-uuencode
> >
> >
>
> com...
> Your ropes hang that way?
>
>
> Duncan Adamson wrote:
> > OK, I am sold on iso-surfaces. A long time project of mine has been to
> > create a catenoid (minimal surface object created by rotating a catenary
> > (shape a hanging rope makes)).
> >
> > Functions are fantastic. Here it is:
> >
> >
> >
> >
> >
> > catenoid.jpg
> >
> > Content-Type:
> >
> > image/jpeg
> > Content-Encoding:
> >
> > x-uuencode
> >
> >
>
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
"Duncan Adamson" <dja### [at] doc ic ic ac ac uk> wrote in message
news:3bb4754e$1@news.povray.org...
> Hang a rope from two points <0,1,0> and <1,1,0>
> The shape it makes is a caterary
>
> Rotate this shape around the x axis to get a catenoid
>(formula radius =
> (1/a)cosh(ax))
Is this the formula for a caterary or a catenoid? I'm looking for the formula
for a caterary.
Regards,
- Nekar uk> wrote in message
news:3bb4754e$1@news.povray.org...
> Hang a rope from two points <0,1,0> and <1,1,0>
> The shape it makes is a caterary
>
> Rotate this shape around the x axis to get a catenoid
>(formula radius =
> (1/a)cosh(ax))
Is this the formula for a caterary or a catenoid? I'm looking for the formula
for a caterary.
Regards,
- Nekar
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
caternary is of the form
y = (1/a)(cosh(a*x))
where a is a constant
note: this is equivalent to
y = (1/a)((e^(a*x) + e^(-a*x))/2)
where a is a constant
where e is the standard mathematical constant 2.817.....
Duncan
"Nekar Xenos" <j-p### [at] citywalk co co za> wrote in message
news:3bb481e2@news.povray.org...
>
> "Duncan Adamson" <dja### [at] doc za> wrote in message
news:3bb481e2@news.povray.org...
>
> "Duncan Adamson" <dja### [at] doc ic ic ac ac uk> wrote in message
> news:3bb4754e$1@news.povray.org...
> > Hang a rope from two points <0,1,0> and <1,1,0>
> > The shape it makes is a caterary
> >
> > Rotate this shape around the x axis to get a catenoid
>
> >(formula radius =
> > (1/a)cosh(ax))
>
> Is this the formula for a caterary or a catenoid? I'm looking for the
formula
> for a caterary.
>
> Regards,
>
> - Nekar
>
>
> uk> wrote in message
> news:3bb4754e$1@news.povray.org...
> > Hang a rope from two points <0,1,0> and <1,1,0>
> > The shape it makes is a caterary
> >
> > Rotate this shape around the x axis to get a catenoid
>
> >(formula radius =
> > (1/a)cosh(ax))
>
> Is this the formula for a caterary or a catenoid? I'm looking for the
formula
> for a caterary.
>
> Regards,
>
> - Nekar
>
>
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Here is a very well rounded list of physical constants
http://www.alcyone.com/max/reference/physics/constants.html
Duncan Adamson wrote:
> caternary is of the form
>
> y = (1/a)(cosh(a*x))
> where a is a constant
>
> note: this is equivalent to
> y = (1/a)((e^(a*x) + e^(-a*x))/2)
> where a is a constant
> where e is the standard mathematical constant 2.817.....
>
> Duncan
>
> "Nekar Xenos" <j-p### [at] citywalk co co za> wrote in message
> news:3bb481e2@news.povray.org...
> >
> > "Duncan Adamson" <dja### [at] doc za> wrote in message
> news:3bb481e2@news.povray.org...
> >
> > "Duncan Adamson" <dja### [at] doc ic ic ac ac uk> wrote in message
> > news:3bb4754e$1@news.povray.org...
> > > Hang a rope from two points <0,1,0> and <1,1,0>
> > > The shape it makes is a caterary
> > >
> > > Rotate this shape around the x axis to get a catenoid
> >
> > >(formula radius =
> > > (1/a)cosh(ax))
> >
> > Is this the formula for a caterary or a catenoid? I'm looking for the
> formula
> > for a caterary.
> >
> > Regards,
> >
> > - Nekar
> >
> >
> > uk> wrote in message
> > news:3bb4754e$1@news.povray.org...
> > > Hang a rope from two points <0,1,0> and <1,1,0>
> > > The shape it makes is a caterary
> > >
> > > Rotate this shape around the x axis to get a catenoid
> >
> > >(formula radius =
> > > (1/a)cosh(ax))
> >
> > Is this the formula for a caterary or a catenoid? I'm looking for the
> formula
> > for a caterary.
> >
> > Regards,
> >
> > - Nekar
> >
> >
> >
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Ahh, a rope from two points... I ass-u-me d one!
Duncan Adamson wrote:
> Hang a rope from two points <0,1,0> and <1,1,0>
> The shape it makes is a caterary
>
> Rotate this shape around the x axis to get a catenoid (formula radius =
> (1/a)cosh(ax))
>
> My catenoid has been rotated to stand on its end.
>
> Duncan
>
> "Is" <mee### [at] yahoo com> wrote in message news:3BB### [at] yahoo com> wrote in message news:3BB### [at] yahoo com...
>
>>Your ropes hang that way?
>>
>>
>>Duncan Adamson wrote:
>>
>>>OK, I am sold on iso-surfaces. A long time project of mine has been to
>>>create a catenoid (minimal surface object created by rotating a catenary
>>>(shape a hanging rope makes)).
>>>
>>>Functions are fantastic. Here it is:
>>>
>>>
>>>
>>>
>>>
>>>catenoid.jpg
>>>
>>>Content-Type:
>>>
>>>image/jpeg
>>>Content-Encoding:
>>>
>>>x-uuencode
>>>
>>>
>>>
>>
>
> com...
>
>>Your ropes hang that way?
>>
>>
>>Duncan Adamson wrote:
>>
>>>OK, I am sold on iso-surfaces. A long time project of mine has been to
>>>create a catenoid (minimal surface object created by rotating a catenary
>>>(shape a hanging rope makes)).
>>>
>>>Functions are fantastic. Here it is:
>>>
>>>
>>>
>>>
>>>
>>>catenoid.jpg
>>>
>>>Content-Type:
>>>
>>>image/jpeg
>>>Content-Encoding:
>>>
>>>x-uuencode
>>>
>>>
>>>
>>
>
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Q: How do you make a catenoid?
A: Pull its tail.
I can't remember where I heard that one, probably somewhere on the net. I
agree with you on isosurfaces, they're fantastic!
~Kevin Wampler~
Duncan Adamson wrote:
> OK, I am sold on iso-surfaces. A long time project of mine has been to
> create a catenoid (minimal surface object created by rotating a catenary
> (shape a hanging rope makes)).
>
> Functions are fantastic. Here it is:
>
> [Image]
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I'll have to remember that one! But only for people who know what a catenoid
is - Explaining this joke would ruin any chance of getting a laugh (or
groan).
"Kevin Wampler" <kev### [at] tapestry tucson tucson az az us> wrote in message
news:3BB4A2A6.72B562AE@tapestry.tucson.az.us...
> Q: How do you make a catenoid?
>
> A: Pull its tail.
>
> I can't remember where I heard that one, probably somewhere on the net. I
> agree with you on isosurfaces, they're fantastic!
>
> ~Kevin Wampler~
>
> Duncan Adamson wrote:
>
> > OK, I am sold on iso-surfaces. A long time project of mine has been to
> > create a catenoid (minimal surface object created by rotating a catenary
> > (shape a hanging rope makes)).
> >
> > Functions are fantastic. Here it is:
> >
> > [Image]
> us> wrote in message
news:3BB4A2A6.72B562AE@tapestry.tucson.az.us...
> Q: How do you make a catenoid?
>
> A: Pull its tail.
>
> I can't remember where I heard that one, probably somewhere on the net. I
> agree with you on isosurfaces, they're fantastic!
>
> ~Kevin Wampler~
>
> Duncan Adamson wrote:
>
> > OK, I am sold on iso-surfaces. A long time project of mine has been to
> > create a catenoid (minimal surface object created by rotating a catenary
> > (shape a hanging rope makes)).
> >
> > Functions are fantastic. Here it is:
> >
> > [Image]
>
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On Fri, 28 Sep 2001 14:01:09 +0100, "Duncan Adamson"
<dja### [at] doc ic ic ac ac uk> wrote:
>Hang a rope from two points <0,1,0> and <1,1,0>
>The shape it makes is a caterary
Isn't it a parabola?
Peter Popov ICQ : 15002700
Personal e-mail : pet### [at] vip uk> wrote:
>Hang a rope from two points <0,1,0> and <1,1,0>
>The shape it makes is a caterary
Isn't it a parabola?
Peter Popov ICQ : 15002700
Personal e-mail : pet### [at] vip bg
TAG e-mail : pet### [at] tag bg
TAG e-mail : pet### [at] tag povray povray org org
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |




![]()