|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
So, Here's where I am and what I'm thinking:
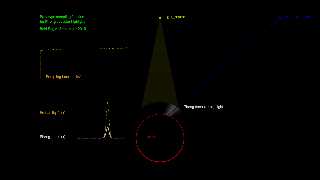
I was able to model a phong highlight on a circle - with the incident light rays
in yellow and the camera look_at vector in blue.
I color the outgoing reflected rays as I, the intensity of the cosine of the
angle between the reflected ray and the camera, to the Nth power.
The graph shows I in white, and the integral of the Phong specular reflection
function in orange.
Then I was trying to think of a way to make the likelihood of choosing an x
value proportional to its corresponding y value.
It occurred to me that if one were to sort of cut the graph down the center of
the peak, and then flip both halves around the diagonal to do a sort of matrix
transposition where x was y and y was x, then as the peak rose, the transposed
graph would "widen" in its x dimension, which would make a random sampling in
that area proportional to its y value.
(I think there's a more sophisticated way to do this than what I currently have,
and I need to figure out how to calculate the linear / "arc" length of a curve
to do some more experiments)
As you can see from the top graph, the region corresponding to the specular
highlight dominates the graph, and the sides are hardly represented at all.
I think if I can figure out how to take the expanded ascissa of the upper graph,
map the original y values back onto that, and the normalize it, then that would
yield the type of function you'd want to sample from.
I think that could probably be done mathematically, rather than graphically, but
I think I need to think about a few things including second derivatives. net> wrote:
So, Here's where I am and what I'm thinking:
I was able to model a phong highlight on a circle - with the incident light rays
in yellow and the camera look_at vector in blue.
I color the outgoing reflected rays as I, the intensity of the cosine of the
angle between the reflected ray and the camera, to the Nth power.
The graph shows I in white, and the integral of the Phong specular reflection
function in orange.
Then I was trying to think of a way to make the likelihood of choosing an x
value proportional to its corresponding y value.
It occurred to me that if one were to sort of cut the graph down the center of
the peak, and then flip both halves around the diagonal to do a sort of matrix
transposition where x was y and y was x, then as the peak rose, the transposed
graph would "widen" in its x dimension, which would make a random sampling in
that area proportional to its y value.
(I think there's a more sophisticated way to do this than what I currently have,
and I need to figure out how to calculate the linear / "arc" length of a curve
to do some more experiments)
As you can see from the top graph, the region corresponding to the specular
highlight dominates the graph, and the sides are hardly represented at all.
I think if I can figure out how to take the expanded ascissa of the upper graph,
map the original y values back onto that, and the normalize it, then that would
yield the type of function you'd want to sample from.
I think that could probably be done mathematically, rather than graphically, but
I think I need to think about a few things including second derivatives.
Post a reply to this message
Attachments:
Download 'phong_model.png' (54 KB)
Preview of image 'phong_model.png'
|
 |




![]()