 |
 |
|
 |
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
I am once again projecting the sRGB gamut into xyY space. This time,
however, I am generating a mesh parametrically instead of creating an
isosurface.
All goes well until R, G and B are all equal to zero, since xyY space
doesn't like this coordinate.
How should I handle this case? Should I just skip it and not render a
triangle there? Or is there a better way to handle it?
Thanks!
Mike
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 29.03.2017 um 04:36 schrieb Mike Horvath:
> I am once again projecting the sRGB gamut into xyY space. This time,
> however, I am generating a mesh parametrically instead of creating an
> isosurface.
>
> All goes well until R, G and B are all equal to zero, since xyY space
> doesn't like this coordinate.
>
> How should I handle this case? Should I just skip it and not render a
> triangle there? Or is there a better way to handle it?
My recommendation would be to go as close to 0 as you can (e.g. 1e-6).
If you feel like it, you can add some hard-coded triangles from there to
(x,y,Y)=(0,0,0) to get a closed shape.
Post a reply to this message
|
 |
|  |
|  |
|
 |
From: Mike Horvath
Subject: Re: Projecting sRGB gamut into xyY space
Date: 29 Mar 2017 19:59:07
Message: <58dc4a4b@news.povray.org>
|
|
 |
|  |
|  |
|
 |
On 3/29/2017 12:18 PM, clipka wrote:
> Am 29.03.2017 um 04:36 schrieb Mike Horvath:
>> I am once again projecting the sRGB gamut into xyY space. This time,
>> however, I am generating a mesh parametrically instead of creating an
>> isosurface.
>>
>> All goes well until R, G and B are all equal to zero, since xyY space
>> doesn't like this coordinate.
>>
>> How should I handle this case? Should I just skip it and not render a
>> triangle there? Or is there a better way to handle it?
>
> My recommendation would be to go as close to 0 as you can (e.g. 1e-6).
> If you feel like it, you can add some hard-coded triangles from there to
> (x,y,Y)=(0,0,0) to get a closed shape.
>
Plotting the triangles to (x,y,Y)=(0,0,0) or very near there is not
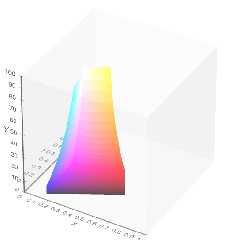
going to produce nice/correct results. See the attached image. Those
triangles would look very much out of place.
Mike
Post a reply to this message
Attachments:
Download 'cie_srgb_gamut_xyy_space_cube_mesh000.png' (37 KB)
Preview of image 'cie_srgb_gamut_xyy_space_cube_mesh000.png'
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
Am 30.03.2017 um 01:59 schrieb Mike Horvath:
> On 3/29/2017 12:18 PM, clipka wrote:
>> Am 29.03.2017 um 04:36 schrieb Mike Horvath:
>>> I am once again projecting the sRGB gamut into xyY space. This time,
>>> however, I am generating a mesh parametrically instead of creating an
>>> isosurface.
>>>
>>> All goes well until R, G and B are all equal to zero, since xyY space
>>> doesn't like this coordinate.
>>>
>>> How should I handle this case? Should I just skip it and not render a
>>> triangle there? Or is there a better way to handle it?
>>
>> My recommendation would be to go as close to 0 as you can (e.g. 1e-6).
>> If you feel like it, you can add some hard-coded triangles from there to
>> (x,y,Y)=(0,0,0) to get a closed shape.
>>
>
> Plotting the triangles to (x,y,Y)=(0,0,0) or very near there is not
> going to produce nice/correct results. See the attached image. Those
> triangles would look very much out of place.
The "closure" to (0,0,0) was only suggested as a final add-on.
What you need to do is take R,G,B to a very small value (e.g. 1e-6)
separately.
It may be sufficient to plot the (distorted) cube as usual, but every
time /any/ R,G,B coordinate drops to zero you replace that value with
1e-6 instead.
Then again maybe that's not enough, and you may need to increase your
cube's resolution near (0,0,0).
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
>> My recommendation would be to go as close to 0 as you can (e.g. 1e-6).
>> If you feel like it, you can add some hard-coded triangles from there to
>> (x,y,Y)=(0,0,0) to get a closed shape.
>>
>
> Plotting the triangles to (x,y,Y)=(0,0,0) or very near there is not
> going to produce nice/correct results. See the attached image. Those
> triangles would look very much out of place.
In my mind, the point RGB=0,0,0 corresponds to the surface that "caps"
the bottom of your 3D shape. ie the one where Y=0 and is bordered by the
classic "horseshoe". Any point on that "cap" would be RGB=0 because Y=0.
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|  |
|
 |
On 4/3/2017 8:18 AM, scott wrote:
>>> My recommendation would be to go as close to 0 as you can (e.g. 1e-6).
>>> If you feel like it, you can add some hard-coded triangles from there to
>>> (x,y,Y)=(0,0,0) to get a closed shape.
>>>
>>
>> Plotting the triangles to (x,y,Y)=(0,0,0) or very near there is not
>> going to produce nice/correct results. See the attached image. Those
>> triangles would look very much out of place.
>
> In my mind, the point RGB=0,0,0 corresponds to the surface that "caps"
> the bottom of your 3D shape. ie the one where Y=0 and is bordered by the
> classic "horseshoe". Any point on that "cap" would be RGB=0 because Y=0.
>
I couldn't figure out what values to use for x and y, so I just skipped
those points.
Mike
Post a reply to this message
|
 |
|  |
|  |
|
 |
|
 |
|  |
|
 |




![]()