"Bald Eagle" <cre### [at] netscapenet> wrote:

> I just started watching Daniel Schiffman's video this morning - I was hoping to
> start writing some code based on it after work.

Well, I got partway there.
I'm botching _something_ up (as usual).

I need to stop blindly hacking and do some more thinking and learning.


#version 3.8;
global_settings {assumed_gamma 1.0 }

#declare S3 = sqrt(3);

#declare M = 3;
#declare C1 = < 1,  0,  1>+M*(x+y);
#declare C2 = <-1,  0,  1>+M*(x+y);
#declare C3 = < 0, S3,  1>+M*(x+y);


camera {
 location M*<1, S3/2, -2.25>
 right x*image_width/image_height
 up y
 look_at M*<1, S3/2, 0>
 //rotate y*15
}
sky_sphere {pigment {rgb 1}}
light_source {< 0, 0, -150> rgb 1}

#declare Line = 0.005;

cylinder {-x*100, x*100, Line pigment {rgb x}}
cylinder {-y*100, y*100, Line pigment {rgb y}}

#declare k4curvature1 = function (k1, k2, k3) {k1 + k2 + k3 + 2 * sqrt (k1*k2 +
k2*k3 + k3*k1)}
#declare k4curvature2 = function (k1, k2, k3) {k1 + k2 + k3 - 2 * sqrt (k1*k2 +
k2*k3 + k3*k1)}



// Make every circle a vector: <Real, Imaginary, Radius>
// Start out with <R, I, 0> to do math, and then tack on radius in last step
// That way add, subtract, and scalar multiplication are all just operations on
a vector

#macro Re(Z) Z.x #end
#macro Im(Z) Z.y #end
#macro Mult(z1, z2) <Re(z1)*Re(z2) - Im(z1)*Im(z2), Re(z1)*Im(z2) +
Im(z1)*Re(z2)> #end

#macro Sqrt (Z)
 #local m = sqrt ( Re(Z)*Re(Z) + Im(Z)*Im(Z) );
 #local Angle = atan2 (Im(Z), Re(Z)) / 2;
 #local NewZ = sqrt(m)*<cos(Angle), sin(Angle)>;
 NewZ
#end

#macro ComplexDescartes (C1, C2, C3, k4)
 // z41 = (z1*k1 + z2*k2 + z3*k3 + 2 * sqrt (z1*k1*z2*k2 + z2*k2*z3*k3 +
z3*k3*z1*k1)) / k4
 // z42 = (z1*k1 + z2*k2 + z3*k3 - 2 * sqrt (z1*k1*z2*k2 + z2*k2*z3*k3 +
z3*k3*z1*k1)) / k4
 #local k1 = 1/C1.z;
 #local k2 = 1/C2.z;
 #local k3 = 1/C3.z;

 #local z1 = <C1.x, C1.y>;
 #local z2 = <C2.x, C2.y>;
 #local z3 = <C3.x, C3.y>;

 #local zk1 = z1*k1;
 #local zk2 = z2*k2;
 #local zk3 = z3*k3;

 #local Sum = zk1 + zk2 + zk3;
 #local Square = Mult (zk1, zk2) + Mult (zk2, zk3) + Mult (zk3, zk1);
 #local Root = Sqrt (Square);

 #local z41 = (Sum + 2*Root) / k4;
 #local z42 = (Sum - 2*Root) / k4;

 #local Z41 = z41 + <0, 0, 1/k4>;
 #local Z42 = z42 + <0, 0, 1/k4>;

 #local Result = array [2] {Z41, Z42};

 Result
#end

#macro Circle (C)
 torus {abs(C.z), Line pigment {rgb 0} rotate x*90 translate <C.x, C.y, 0>}
#end








#declare k41 = k4curvature1 (1/C1.z, 1/C2.z, 1/C3.z);
#declare k42 = k4curvature2 (1/C1.z, 1/C2.z, 1/C3.z);

#declare C41 = ComplexDescartes (C1, C2, C3, k41);
#declare C42 = ComplexDescartes (C1, C2, C3, k42);

#if (0)
Circle (C1)
Circle (C2)
Circle (C3)
Circle (C41[0])
Circle (C42[1])
#end

#macro DrawCircles (Array)
 #local Circles = dimension_size (Array, 1)-1;
 #for (C, 0, Circles)
  Circle (Array [C])
 #end
#end

#declare AllCircles = array;
#declare AllCircles [0] = C1;
#declare AllCircles [1] = C2;
#declare AllCircles [2] = C3;

#declare Queue = array;
#declare Queue [0] = array [3] {C1, C2, C3};

//#declare Queue [0] = C1;
//#declare Queue [1] = C2;
//#declare Queue [2] = C3;

#declare Levels = 3;

#macro Gasket (RecursionLevels)
 #for (L, 0, RecursionLevels)
  #local Triplets = dimension_size (Queue, 1)-1;
  #for (T, 0, Triplets)
   DrawCircles (Queue [T])
  #end

  #declare NextQueue = array;
  #local QIndex = 0;
  #for (T, 0, Triplets)
   #local triplet = Queue [T];
   #local c1 = triplet [0];
   #local c2 = triplet [1];
   #local c3 = triplet [2];
   #local k41 = k4curvature1 (1/c1.z, 1/c2.z, 1/c3.z);
   #local k42 = k4curvature2 (1/c1.z, 1/c2.z, 1/c3.z);
   #declare new1 = ComplexDescartes (c1, c2, c3, k41);
   #declare new2 = ComplexDescartes (c1, c2, c3, k42);

   #local T1 = array [3] {c1, c2, new1[0]};
   #local T2 = array [3] {c2, c3, new1[1]};
   #local T3 = array [3] {c3, c1, new1[1]};
   #local T4 = array [3] {c1, c2, new2[1]};
   #local T5 = array [3] {c2, c3, new2[1]};
   #local T6 = array [3] {c3, c1, new2[1]};
   //#local T6 = array [3] {c2, c3, new1[1]};

   #declare NextQueue [QIndex] = T1;
   #local QIndex = QIndex + 1;
   #declare NextQueue [QIndex] = T2;
   #local QIndex = QIndex + 1;
   #declare NextQueue [QIndex] = T3;

   #local QIndex = QIndex + 1;
   #declare NextQueue [QIndex] = T4;
   #local QIndex = QIndex + 1;
   #declare NextQueue [QIndex] = T5;
   #local QIndex = QIndex + 1;
   #declare NextQueue [QIndex] = T6;

  #end // end for T

  #declare Queue = NextQueue;
 #end // end for L
#end

Gasket (Levels)

Post a reply to this message

Attachments:
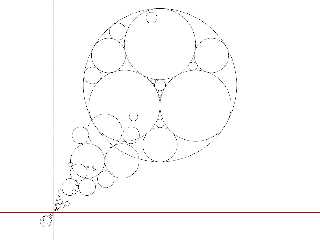
Download 'appolonian_gasket.png' (62 KB)

Preview of image 'appolonian_gasket.png'