|
 |
"Bald Eagle" <cre### [at] netscape net> wrote:
> I still feel like there should be some minus signs in there to make the
> interpolation work - but maybe those pop out the other side of the MInvers () .
> .. . I'll have to write that out in SDL and run it to find out.
Sent values of A-D for each segment to the debug stream, and there are
definitely minus signs.
> I also don't quite understand why we need to take the square root of the result
> in line 1082
> x[n] = sqrt(r[n] * (r[n] * (r[n] * A + B) + C) + D);
> to get the interpolated spline values, but perhaps that may become clear as I
> find more bits of time here and the to properly focus on this.
This apparently has to do with the value of "alpha" in the interpolation, with 0
being Uniform, 1/2 being Centripetal, and 1 being Chordal.
I'm not really sure where "r" comes from in the source, or how that while loop
interpolates the spline, but I just ignored all of that, and things worked out
anyway. :D
After fixing some boneheaded visualization bugs, the math seemed to be working
out with the spline, so I took my SDL version of the SOR spline and used the X
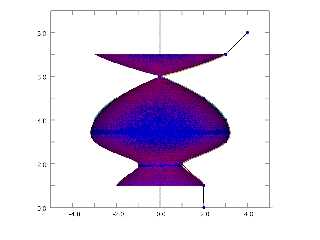
value (minus the minor radius) as the major radius of a torus, and "plotted" a
torus at each interpolation point. (RED)
Seems to overlay the sor {} object (BLUE) very closely. Errors are probably due
to my janky simulation method, and coincident surfaces.
I'll try to work out the details as I write things up, and I'll probably make a
parametric {} and isosurface {} object to further test how well things match up.
- BE net> wrote:
> I still feel like there should be some minus signs in there to make the
> interpolation work - but maybe those pop out the other side of the MInvers () .
> .. . I'll have to write that out in SDL and run it to find out.
Sent values of A-D for each segment to the debug stream, and there are
definitely minus signs.
> I also don't quite understand why we need to take the square root of the result
> in line 1082
> x[n] = sqrt(r[n] * (r[n] * (r[n] * A + B) + C) + D);
> to get the interpolated spline values, but perhaps that may become clear as I
> find more bits of time here and the to properly focus on this.
This apparently has to do with the value of "alpha" in the interpolation, with 0
being Uniform, 1/2 being Centripetal, and 1 being Chordal.
I'm not really sure where "r" comes from in the source, or how that while loop
interpolates the spline, but I just ignored all of that, and things worked out
anyway. :D
After fixing some boneheaded visualization bugs, the math seemed to be working
out with the spline, so I took my SDL version of the SOR spline and used the X
value (minus the minor radius) as the major radius of a torus, and "plotted" a
torus at each interpolation point. (RED)
Seems to overlay the sor {} object (BLUE) very closely. Errors are probably due
to my janky simulation method, and coincident surfaces.
I'll try to work out the details as I write things up, and I'll probably make a
parametric {} and isosurface {} object to further test how well things match up.
- BE
Post a reply to this message
Attachments:
Download 'surface of revolution documentation.png' (255 KB)
Preview of image 'surface of revolution documentation.png'
|
 |




![]()