My attempts to get Wave Function Collapse to work on the irregular grid 
didn't go so well. The wave function collapses the cells and removes all 
possibilities. I either need backtracking or I need to figure out how to 
overlap tiles.

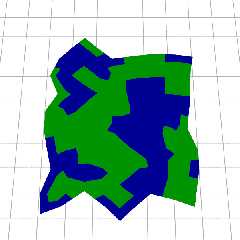
So I tried marching squares instead. I have discovered my original tile 
set is deficient so I need to add one more tile. However, I found a 
configuration that lets me use this algorithm.

The idea is each point is given a calculated value, and each 4-sided 
cell is then determined by the values of the four corners. With only two 
choices for each point, I can calculate a value of 0 to 15 and map to 
one of my tiles.

Here is a sample that avoids the gaps in my tileset.

Documentation and clean code one day, I promise.

Josh

Post a reply to this message

Attachments:
Download 'marching_cubes_graph.png' (37 KB)

Preview of image 'marching_cubes_graph.png'